Graficzna prezentacja danych ma dużą siłę przekazu. Większości osób łatwiej zapamiętać obraz niż tabelę z liczbami. O ile jednak trudno o zniekształcenie percepcji danych, gdy prezentowane są jako tabela z liczbami (oczywiście o ile liczby są prawdziwe), o tyle percepcja wykresu zależy od wielu czynników, którymi można wpływać na końcowy odbiór. Wpływać celowo lub przypadkowo. Aby uniknąć przypadkowych zniekształceń, trzeba przyłożyć jak największą staranność do prezentacji danych, by pokazać tylko istniejące zależności.
Nie zawsze udaje się to osiągnąć. W pewnych sytuacjach obraz staje się niespójny z danymi, które ma prezentować. Bywa, że wykres zawiera zarówno liczby, jak i elementy graficzne je opisujące. Co się dzieje, gdy te dwa komunikaty są niespójne?
Najczęściej pierwszy odczytywany jest komunikat graficzny. Jeżeli jest taka potrzeba lub odbiorca jest bardzo dociekliwy, to jako kolejny jest interpretowany komunikat liczbowy – ze swojej natury wymagający większej uwagi i trudniejszy do interpretacji. Jeżeli komunikat graficzny jest czytelny i spójny, to zostanie zapamiętany, nawet jeżeli nie ma pokrycia w danych. W przypadku, gdy wykryjemy, że te dwa komunikaty się różnią, wciąż jesteśmy bardziej skłonni zapamiętać komunikat oparty o elementy graficzne.
Ciekawą ilustracją, jak bardzo czytelność komunikatu wpływa na jego wiarygodność, jest eksperyment przedstawiony w książce Pułapki myślenia Daniela Kahnemana. Eksperyment jest następujący. Należy wybrać, która z poniższych wypowiedzi jest prawdziwa.
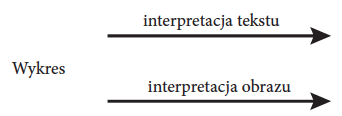 Rysunek 1: Dwie ścieżki odczytywania komunikatów z wykresu przez mózg
Rysunek 1: Dwie ścieżki odczytywania komunikatów z wykresu przez mózg

Jest to sytuacja, w której docierają do nas dwa sprzeczne komunikaty. Jeżeli nie wiemy, który z nich jest prawdziwy, to większość osób za bardziej wiarygodny uzna ten, który jest graficznie czytelniejszy. Im bardziej poznawczo obciążony jest nasz umysł, tym większa szansa, że ocenę wiarygodności oprzemy wyłącznie na czytelności komunikatu. Osoba zmęczona kilkoma godzinami wysiłku umysłowego jest bardziej podatna na tego typu manipulacje. Jej system krytycznego myślenia jest bowiem wyczerpany.
Wiedząc jak bardzo graficzne elementy są ważne dla wizualizacji danych, warto poznać typowe problemy, przez które postrzeganie danych jest celowo lub przypadkowo zniekształcane. W literaturze znaleźć można wiele przykładów wykresów, które przekłamują lub zniekształcają relacje opisane przez dane. Jednym z ciekawych źródeł takich przykładów jest portal DataVis (DataVis: Practical steps for improving visualisation, http://bit.ly/1lCmVcF). Fundacja SmarterPoland.pl organizuje co roku plebiscyt, w którym internauci wybierają najgorszą w danym roku krajową prezentację danych. Najgorszą w sensie najbardziej wypaczającą rzeczywiste zależności zawarte w danych.
Zarówno w edycji konkursu z roku 2012 jak i w przypadku edycji z roku 2013 wybór nie był prosty, a kandydatów do nagrody wielu. Typowe problemy dotyczą niepoprawnego użycia długości przy korzystaniu z wykresów paskowych, użycia perspektywy imitującej trzeci wymiar, niepoprawnego użycia pól do prezentacji zależności pomiędzy danymi oraz użycia niewłaściwych narzędzi do przedstawienia zależność pomiędzy danymi. Omówimy te problemy na przykładach.
Długość paska ma znaczenie
Jednym z częstszych problemów jest używanie wykresów paskowych lub ich rozmaitych odmian bez zadbania o to, by pasek zaczynał się w punkcie zero. Należy pamiętać, że porównując paski domyślnie porównujemy proporcje długości. Spodziewamy się, że jeżeli jeden pasek jest dwukrotnie dłuższy od drugiego, to odpowiada dwukrotnie większej wartości.
Często jednak się zdarza, że paski nie są przedstawiane w całości, a punkt zero znajduje się poza wykresem, co stwarza duże pole do manipulacji. Przesuwając początek paska w kierunku wartości dodatnich, uwypuklamy różnice pomiędzy wielkościami, a przesuwając w kierunku ujemnym tę różnicę optycznie zmniejszamy.

Przykładem, w którym to zniekształcenie jest bardzo wyraźne, jest wykres z artykułu Drożejąca energia podnosi koszty utrzymania mieszkań, w którym koszt użytkowania nieruchomości na osobę przedstawiony jest za pomocą pasków zaczynających się w wartości 200 (czego trzeba się domyślać, ponieważ oś pionowa nie jest przedstawiona).
Rysunek 3: Porównanie uposażenia posła w 2014 roku (9892 zł) bez diet, dodatków, ryczałtów itp. z minimalną gwarantowaną pensją dla profesora zwyczajnego w 2015 roku (5390 zł) bez dodatków za funkcje, bonusy itp. Na górnym wykresie oba słupki zaczynają się w punkcie 0, na środkowym w punkcie 2000, a na dolnym w punkcie -5000. Za każdym razem mamy inne wrażenie dotyczące tych dwóch wielkości. Źródło: opracowanie własne
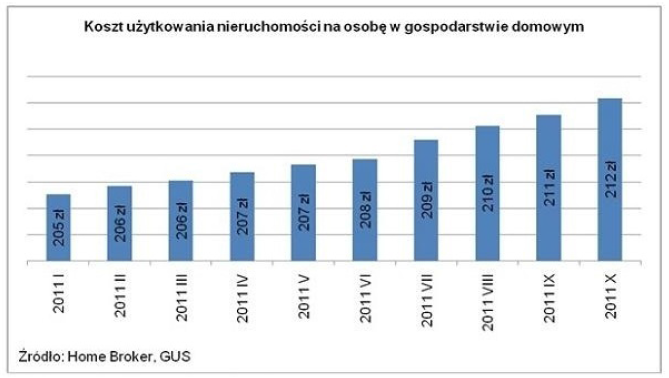
Patrząc na ten wykres, można odnieść wrażenie, że koszt użytkowania nieruchomości szybko rośnie, co jest zgodne z treścią artykułu. Nie jest jednak zgodne z liczbami przedstawionymi na wykresie. W skali dziewięciu miesięcy wzrost o 3,4% był porównywalny z inflacją, ale wykres sugeruje znacznie poważniejszy wzrost cen, skoro długość słupka, przedstawiająca koszty, zwiększyła się przeszło dwukrotnie
Rysunek 4: Wykres przedstawiający średnie osobowe koszty użytkowania nieruchomości w różnych miesiącach roku 2011. Źródło: artykuł Drożejąca energia podnosi koszty utrzymania mieszkań z serwisu
biznes.plJest to przykład skrajny, ale nie odosobniony. Jego skrajność staje się wręcz usprawiedliwieniem. O ile bowiem w przypadku wykresu z portalu gazety internetowej nikt, kto się chwilę nad nim zastanowi, nie uzna długości za dobrą miarę, to zdarzają się wykresy w których przesunięcie początku osi jest trudniejsze do wykrycia.
Przykładem są wykresy z artykułu Przegląd funkcjonowania systemu emerytalnego opracowanego przez Ministerstwo Pracy i Polityki Społecznej.
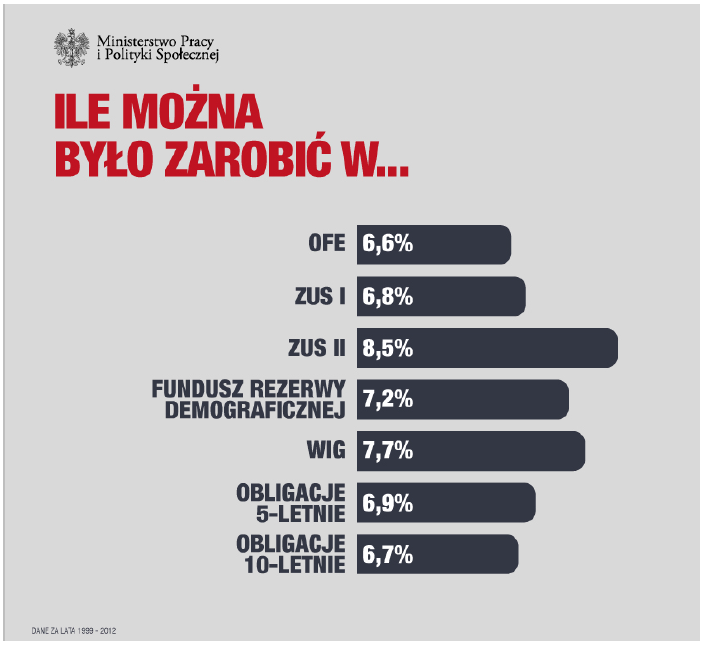
Jeżeli porównamy wielkości odpowiadające temu, ile można “zarobić” w przypadku pozycji OFE i ZUS II, okaże się, że długości słupków odpowiadają stosunkowi 100:168. W rzeczywistości dane wskazują na stosunek 100:129.
Słupki na tym wykresie zniekształcają nasze wyobrażenie o różnicach pomiędzy ZUS II a OFE. Ponieważ na wykresie brakuje osi, jedynym sposobem, by wykryć to zniekształcenie, jest zmierzenie długości obu słupków linijką, czego oczywiście zdecydowana większość czytelników nie robi.
Na granicy poprawności są grafiki, które nie są wykresami, ale aspirują do miana prezentacji danych. Ciekawym przykładem jest wykres przedstawiający poziom dofinansowania na zakup podręczników [Serwis premier.gov.pl. Wyprawka szkolna, 2012]. Prezentuje on kwotę dofinansowania z trzech lat za pomocą rosnącej sterty podręczników. Ta sterta sprawia wrażenie dwa razy większej w roku 2012 niż w roku 2010, co może sugerować, że wielkość dofinansowania wzrosła znacząco, a może nawet, że liczba podręczników, które udało się kupić jest znacznie większa.

Okazuje się jednak, że wzrost nakładów na podręczniki, który wynika z danych to 11% rocznie. I jest to wzrost niższy niż ceny podręczników rosnące szybciej (zgodnie z niektórymi szacunkami drożejące w tempie 15% na rok).
Odczytując tę grafikę dosłownie, widać dużą rozbieżność pomiędzy zwiększeniem nakładów na zakup podręczników a wyobrażeniami o tym zwiększeniu przedstawianymi przez wykres. Czy jednak jest to grafika statystyczna, czy swobodna graficzna impresja, która nie musi przedstawiać danych? Czy jest to przykład dozwolonego użycia metafory wykresu słupkowego bez dbania o rzetelność prezentacji danych, która powinna charakteryzować wykresy, to rzecz dyskusyjna.
Kolejność ma znaczenie
Nie tylko długość słupka odgrywa znaczenie w sposobie percepcji danych, również kolejność lub ustawienie słupków znacząco wpływa na nasze postrzeganie.
Rysunek 6 przedstawia wyniki sondażu preferencji przed wyborami prezydenckimi. Czy wyniki sondaży dla Bronisława Komorowskiego są lepsze, niż w poprzednim miesiącu, czy gorsze? Przykład ten w jaskrawy sposób pokazuje jak ważna rolę odgrywa kolejność słupków na wykresie. Jeżeli czytamy ten wykres nie zagłębiając się w legendę, można odnieść wrażenie, że poparcie dla Bronisława Komorowskiego rośnie. Jednak gdy przyjrzeć się legendzie, okazuje się, że prawy, niebieski słupek to poparcie w styczniu a lewy w lutym. Na tym wykresie czas biegnie w lewą stronę! Zmienia to całkowicie percepcje wzrostu lub spadku poparcia i wiele osób czytających ten wykres wprowadziło w błąd.
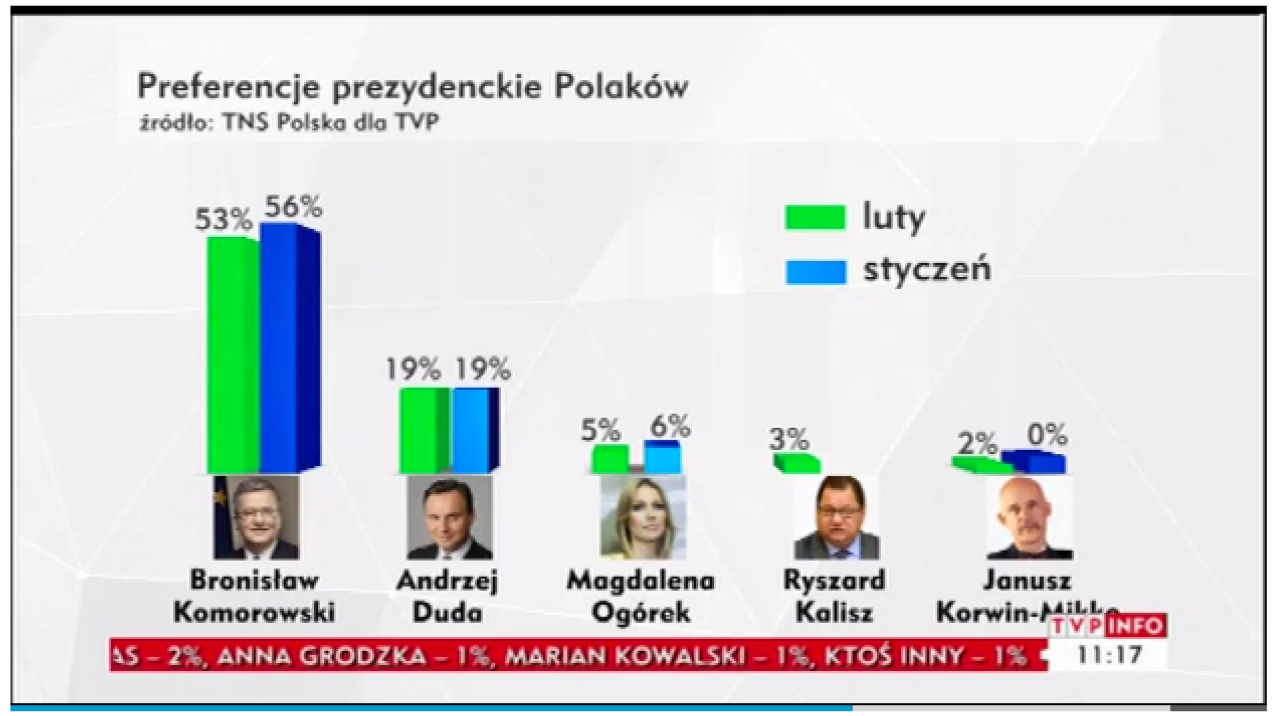
Inną ciekawą ilustracją efektu kolejności jest wykres z artykułu Mieszkań więcej niż kupujących. Ceny mogą jeszcze spaść prezentowanego przez portal wyborcza.biz.
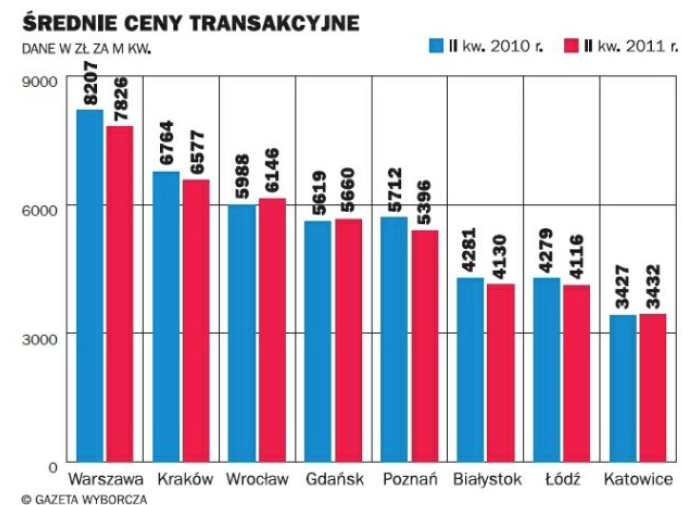
Pierwsze wrażenie z analizy tego wykresu to znaczne spadki cen transakcyjnych. Przekornie można odczytać ten wykres jako przedstawiający spadki z 8207 złotych do 3432 złotych, tyle że 8207 zł to cena z roku 2010 z Warszawy, a 3432 zł to cena z roku 2011 z Katowic.
Rysunek 7: Wykres prezentujący średnie ceny transakcyjne w 2010 i 2011 roku w wybranych miastach w Polsce. Źródło: artykuł Mieszkań więcej niż kupujących. Ceny mogą jeszcze spaść na portalu “Gazety Wyborczej”
Oczywiście przyglądając się dokładniej, dostrzeżemy że zmiany te są mniejsze, ale wrażenie i wpływ tego wrażenia na to, jak zapamiętamy te dane, pozostanie. Patrząc na ten wykres, trudniej też zauważyć, że w przypadku trzech na osiem miast ceny w rzeczywistości wzrosły (Wrocław, Gdańsk, Katowice), a nawet w mieście w którym te ceny spadły najsilniej (Poznań), spadek wyniósł mniej niż 6%.
Zmieniając kolejność słupków lub sposób prezentacji, możemy bardzo zmienić postrzeganą wielkość tych wzrostów/spadków.
O ile poprzedni wykres pokazywał historię, której nie wspierały dane, są też wykresy, które nie pokazują historii sugerowanej przez dane. Przykładem jest wykres 8 z artykułu Więcej mieszkań w lepszej cenie [Serwis http://www.ekonomia.rp.pl/]
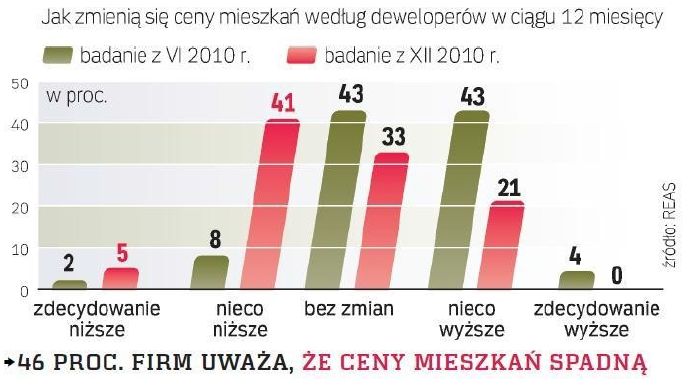
Przedstawicieli film deweloperskich zapytano, jak ich zdaniem zmienią się ceny mieszkań. Odpowiedzi udzielano w skali “zdecydowanie niższe”, “nieco niższe”, “bez zmian”, “nieco wyższe” i “zdecydowanie wyższe”. Z wykresu 8 trudno odczytać, co się z tymi mieszkaniami będzie działo, dopiero po dokładniejszej analizie można stwierdzić, że więcej osób uważa, że ceny będą nieco niższe.
Rysunek 8: Wykres prezentujący prognozy deweloperów co do cen mieszkań w czerwcu i grudniu 2010 roku. Źródło: artykuł Więcej mieszkań w lepszej cenie z portalu “Rzeczpospolitej”
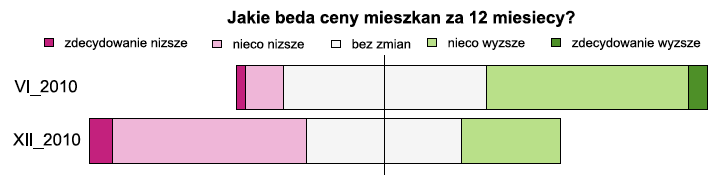
Rysunek 9: Wykres przedstawiające te same dane co rysunek 8, ale z użyciem innego sposobu prezentacji. Na pierwszy rzut oka widać, że oczekiwania co do cen się obniżyły. Źródło: opracowanie własne
Tymczasem dane w skali Likerta można przedstawiać za pomocą tak zwanych “tonących” prostokątów, wyśrodkowanych względem elementu neutralnego. Z takiej postaci znaczenie łatwiej odczytać, jak wyglądały oczekiwania co do wzrostów i spadków w obu przedziałach czasowych.
Pseudo-perspektywa jest szkodliwa
Równie częstym błędem przy prezentacji danych, zaciemniającym obraz, a w niczym niepomagającym, jest dodawanie pseudo trzeciego wymiaru lub perspektywy. Trudno znaleźć jakiekolwiek racjonalne uzasadnienie dla tego typu działań poza chęcią udziwnienia wykresu. Niestety takie zabiegi są wciąż dosyć częste.
Jednym z wyraźniejszych przykładów, jak szkodliwa może być taka udawana głębia wykresu, jest ilustracja z raportu GUS Wejście ludzi młodych na rynek pracy. Dobrze, że na tym wykresie umieszczono etykiety liczbowe dla wskaźnika zatrudnienia absolwentów. Bez niego nie dałoby się tych wartości odczytać. Nawet z etykietami trudno uwierzyć, że pasek zaczyna się na wysokości 52,6%, ponieważ rzut pod skosem sprawił, że pasek wygląda na zaczepiony niżej. Sytuacja jest beznadziejna dla drugiego wskaźnika, zatrudnienia wśród uczniów, który wygląda na stały, ale nie sposób powiedzieć, na jakiej jest wysokości.
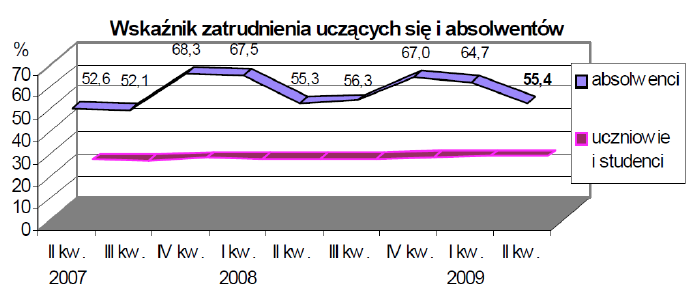
Wykres ten nic nie zyskał przez zastosowanie dodatkowej głębi, a wiele stracił. Zajmuje miejsce w raporcie, ale niewiele pokazuje. Można wręcz powiedzieć, że znacznie bardziej czytelna byłaby sama tabela z liczbami.
Przyjrzyjmy się teraz kolejnemu wykresowi, z raportu Narodowy Spis Powszechny Ludności i Mieszkań 2011 GUS. Ten wykres przedstawia względne wielkości stopy bezrobocia i wskaźnik zatrudnienia.
Rysunek 10: Wykres przedstawiający wskaźnik zatrudnienia młodych ludzi w kolejnych kwartałach lat 2007–2009. Źródło: raport Wejście ludzi młodych na rynek pracy, 2010, Główny Urząd Statystyczny, Departament Pracy
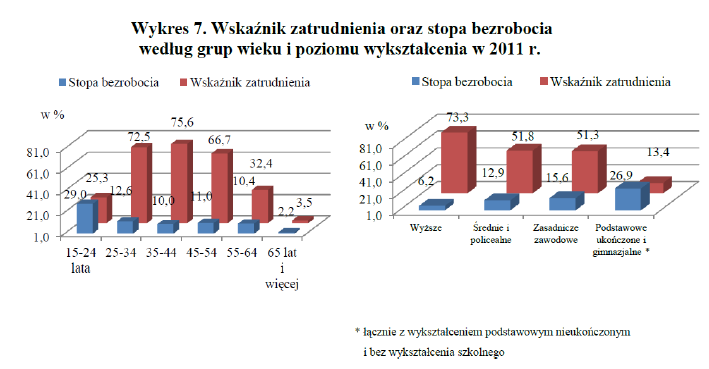
Pierwszą zaskakującą rzeczą jest dziwny dobór linii pomocniczych na wysokościach 1, 21, 41, ..., 81%. Z uwagi na pseudo trzeci wymiar z tych linii nie sposób skorzystać i równie dobrze mogłoby ich nie być.
W tym rzucie trudno zauważyć, że w grupie 15–24 lata stopa bezrobocia jest wyższa niż wskaźnik zatrudnienia, a w grupie osób z wykształceniem podstawowym wskaźnik zatrudnienia jest dwa razy niższy niż stopa bezrobocia.
Gdyby usunąć tę udawaną głębię, nie zmieniając nic innego, znacznie łatwiej byłoby odczytywać wartości z wykresu.
Rysunek 11: Wykres przedstawiający wskaźnik zatrudnienia oraz stopę bezrobocia w różnych grupach wiekowych. Źródło: raport Narodowy Spis Powszechny Ludności i Mieszkań 2011. Raport z wyników Główny Urząd Statystyczny
Obroty, które prowadzą do skrętu kiszek
Ozdobniki można podzielić na dwie grupy: zbędne oraz szkodliwe. Przykładem szkodliwych są wszelkiego rodzaju obroty wykresu powodujące problemy z odczytaniem wartości.
Ciekawym przykładem takiego obrotu, utrudniającego precyzyjne odczytanie wartości, jest wykres z miesięcznika Uniwersytetu Ekonomicznego w Krakowie “Kurier UEK”.
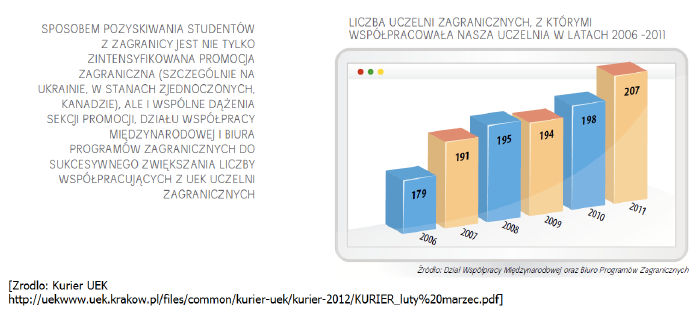
Na wykresie 12 został przesunięty punkt zero. Dodatkowo nachylenie wykresu jak i lekko widoczna rosnąca krzywa mają sugerować dynamiczny wzrost współpracujących uczelni zagranicznych. Rzeczywisty wzrost był na poziomie 15%, co jest samo w sobie dobrym wynikiem, ale ten wykres sugeruje znacznie większe wzrosty, niestety bez pokrycia w danych.
Rysunek 12: Wykres przedstawiający liczbę współpracujących uczelni zagranicznych z Uniwersytetem Ekonomicznym w Krakowie. Źródło: “Kurier UEK”
Kolejnym przykładem takiego pokręconego wykresu jest prezentacja zadłużenia Skarbu Państwa na przełomie dziesięciu lat z zaznaczeniem partii rządzącej na portalu bankier.pl w artykule Gospodarcze osiągnięcia partii politycznych
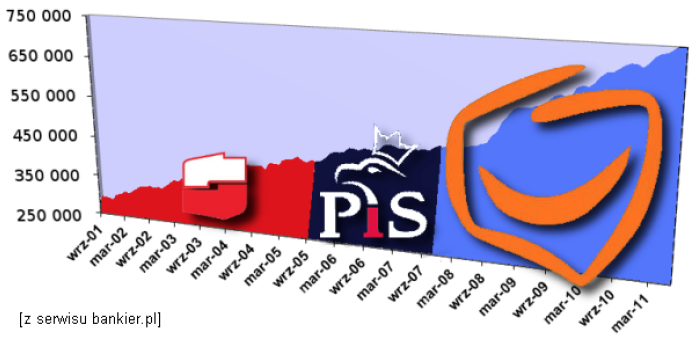
Na tym wykresie jest wiele elementów utrudniających zrozumienie, jak zmieniało się zadłużenie. Dodanie symboli partii, każdego o innej wielkości, już zaburza nasze postrzeganie wykresu. Nie sposób odgadnąć czemu odpowiada wielkość tych symboli i dlaczego te symbole zakrywają wykres.
Pominięcie punktu zerowego utrudnia porównanie wartości bezwzględnych. Trudno odpowiedzieć na pytania typu: ilukrotnie zmieniło się zadłużenie. A obrót wykresu zmniejszający nachylenie utrudnia też poprawne odczytanie, kiedy zadłużenie rosło najszybciej i jak wyglądało to tempo wzrostów.
Rysunek 13: Wykres przedstawiający zadłużenie Skarbu Państwa w milionach złotych. Źródło: artykuł Gospodarcze osiągnięcia partii politycznych z serwisu “Bankier.pl”
Gdyby te dane przedstawić bez zbędnych ozdobników, stosując dodatkowo zasadę 45 stopni, wtedy znacznie łatwiej byłoby zauważyć, kiedy zadłużenie rośnie najszybciej.
Wykresy kołowe są złe
John Tukey ponoć powiedział, że nie ma takich danych, które można przedstawić na wykresie kołowym, ale których nie można przedstawić lepiej za pomocą innego typu wykresu.
Z wykresami kołowymi wiąże się wiele problemów, takich jak trudności w szacowaniu kątów czy powierzchni, które powodują, że koła, choć atrakcyjne wizualnie, są niedokładnym medium prezentacji danych.
Ale o ile jeszcze można znaleźć usprawiedliwienie dla pojedynczego wykresu kołowego, tak nie można znaleźć usprawiedliwiania dla dwóch lub większej liczby wykresów kołowych użytych do porównania wielkości.
Dobrą ilustracją trudności w porównywaniu dwóch wykresów kołowych jest wykres 14 z książki Statystyka od podstaw z systemem SAS wersja 9.2 i 9.3.
Poprawne porównanie kątów czy pól przypisanych różnym województwom jest praktycznie niemożliwe. Województw jest 16, przez co wszystkie wycinki są wąskie i trudno je porównać. Nie wiadomo też, co przedstawiać ma całe koło, sumę średnich wynagrodzeń? To oczywiście skrajny przykład wykresu kołowego z którego trudno coś odczytać. Ale nawet wykresy o mniejszej liczbie poziomów obarczone są podobnymi trudnościami. Porównanie wycinków pomiędzy różnymi wykresami kołowymi jest bardzo trudne.
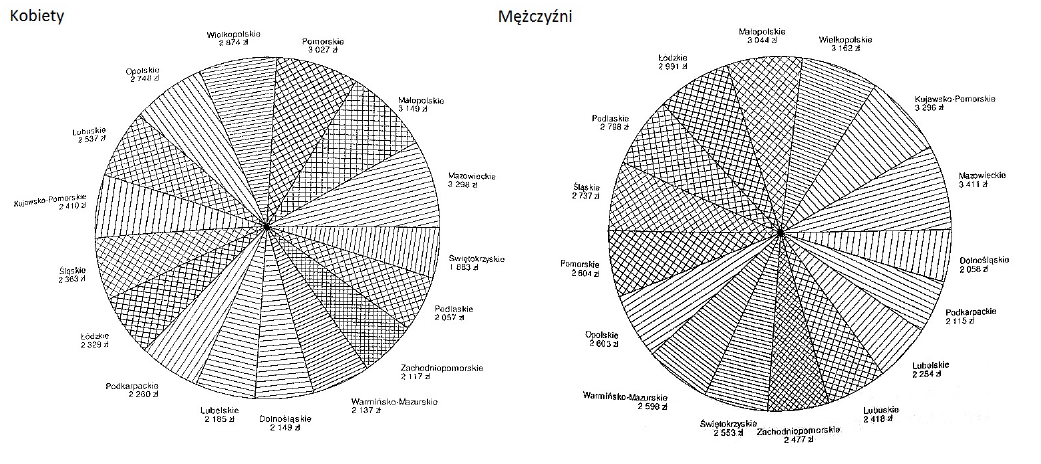 Rysunek 14: Wykres prezentujący średnie wynagrodzenia dla kobiet i mężczyzn w różnych województwach. Źródło: Frątczak E., Korczyński A., Statystyka od podstaw z systemem SAS wersja 9.2 i 9.3, 2013, Wydawnictwo SGH
Rysunek 14: Wykres prezentujący średnie wynagrodzenia dla kobiet i mężczyzn w różnych województwach. Źródło: Frątczak E., Korczyński A., Statystyka od podstaw z systemem SAS wersja 9.2 i 9.3, 2013, Wydawnictwo SGH
Osobny krąg piekła jest prawdopodobnie zarezerwowany dla osób przedstawiających dane za pomocą trójwymiarowych wykresów kołowych.
Dlaczego? Charakterystyką, która przedstawia liczby na wykresach kołowych są kąty, im większa wartość, tym większy kąt. Tymczasem po dodaniu pseudo-trzeciego wymiaru, rzutowanie powoduje, że na wykresie kołowym kąty ulegają zmianie. I im ostrzejszy rzut, im bardziej wykres kołowy zamienia się w wykres elipsowy, tym bardziej proporcje pomiędzy kątami ulegają zniekształceniu. Świetnym przykładem tego zniekształcenia jest wykres 15 z raportu Bio-Info-Techno 2011 Fundacji na rzecz Nauki Polskiej.
Gdyby zmierzyć kąty na przedstawionym wykresie, okazałoby się, że odcinek BIO-INFO jest ponad 2,5 razy węższy niż odcinek BIO-TECHNO, choć oba przedstawiają ten sam udział, czyli 5%. Porównanie odcinków odpowiadających częściom techno i info-techno skutkuje proporcją długości 1,7:1, choć oba wycinki odpowiadają tym samym wartościom, czyli 11%.
Rzut będzie poszerzał kąty bliskie osi pionowej, a zwężał te bliskie osi poziomej. Na przykładzie z wykresu 15 zniekształcenie kątów było ponad dwukrotne.
Dodawanie pseudo-trzeciego wymiaru utrudnia odczytanie każdego rodzaju wykresu, ale żadnego wykresu nie zniekształca tak bardzo jak wykresu kołowego.
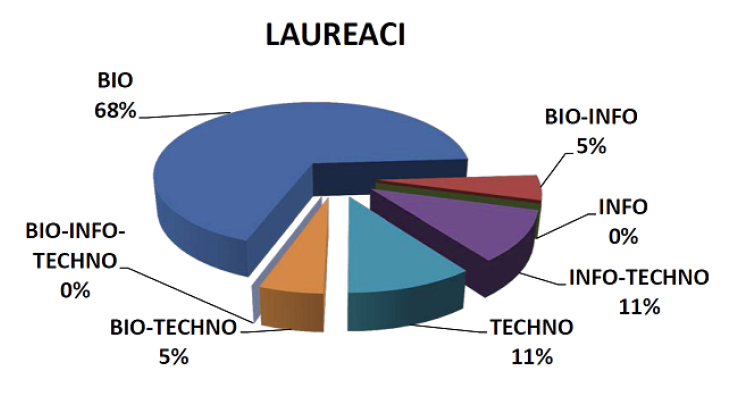
Rysunek 15: Wykres przedstawiający dziedziny reprezentowane przez laureatów jednego z konkursów FNP. Źródło: raport “Bio-Info-Techno 2011” Fundacji na rzecz Nauki Polskiej
Jeżeli to pole, to chyba minowe
Brak odpowiedniości długości słupków i liczb, którym słupki powinny odpowiadać, można odkryć jedynie z użyciem linijki. Trudniej jest, gdy sprawa dotyczy pól. Nasze oko źle ocenia wzajemne stosunki wielkości pól. Ocena wielkości powierzchni jest podatna na sugestie związane z jasnymi intensywnymi kolorami, które optycznie powiększają pola.
Im bardziej nieregularny kształt, tym trudniej ocenić jego pole. Utrudnia to wykrywanie zniekształceń dotyczących przedstawiania pól w innych proporcjach niż sugerują to dane.
Przykładowo, trudno jest zauważyć problem z wykresem 16 pochodzącym ze strony Ministra Finansów [Jacek Rostowski. Piramida finansowa pis, 2013]. Pomijając dobór kolorów i kształtu wykresu (wpływają one na percepcję wielkości pola, niezależnie od tego, jak duże jest to pole w rzeczywistości), okazuje się, że wykres przedstawia inne proporcje niż liczby, które powinien przedstawiać!
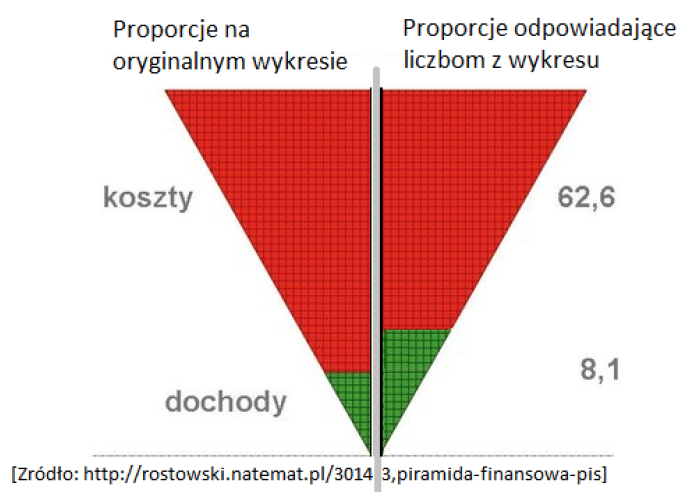
Stosunek dochodów do kosztów, zgodnie z podanymi liczbami, wynosi 8,1/62,6 = 0,1293, podczas gdy po obliczeniu pól obu figur stosunek tych pól wynosi 2 135 punktów/36 903 punktów = 0,0578.
Wykres ten ponad dwukrotnie zniekształca wrażenie dotyczące stosunku dochodu do kosztów. Takie sugestywne zniekształcenie jest trudne w rozszyfrowaniu, nawet gdy mamy linijkę, obliczenie proporcji pól obu figur nie jest zadaniem prostym.
Rysunek 16: Lewa strona to wykres opracowany przez Ministerstwo Finansów z artykułu Piramida finansowa PiS autorstwa Jacka Rostowskiego. Prawa strona pokazuje, jakie proporcje powinny mieć pola zielone i czerwone, by odpowiadały one proporcji liczb. Źródło: lewa połowa serwis Ministerstwa Finansów, prawa połowa opracowanie własne
Używanie pól, nawet nieświadome, może być przyczyną problemów w odczytaniu wykresu. Graficy często używają wielkości symbolu jako cechy opisującej wielkość. Czasem jednak kodują liczby za pomocą wysokości symboli, a czasem za pomocą ich pól. Ale dwukrotnie zwiększona wysokość i szerokość skutkuje czterokrotnym wzrostem pola zajmowanego przez symbol. W sytuacji, gdy nie jest jasne, czy wielkościom odpowiadają pola, czy długości, większość odbiorców intuicyjnie porównuje pola.
Przyjrzyjmy się wykresowi 17 z portalu [Portal biznes.interia.pl. Reforma reformy emerytalnej]. Ocena wielkości ostatniego ludzika w stosunku do pierwszego oparta jest zarówno o postrzeganą intensywność koloru czerwonego, jak i o pole tego ludzika.
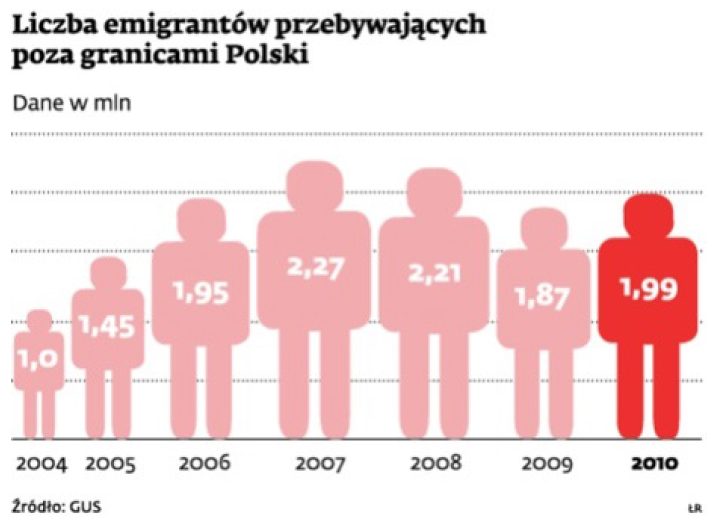
Rysunek 17: Wykres przedstawiający liczbę polskich emigrantów. Źródło: artykuł Reforma reformy emerytalnej. Bo dane się zdezaktualizowały z serwisu
interia.plCelem grafika było przedstawienie dwukrotnie większej liczby emigrantów w roku 2010 niż w roku 2004. Ponieważ jednak ludzika powiększono dwukrotnie na szerokość i wysokość, więc pole jest czterokrotnie większe, a postrzegana względna wielkość jest dodatkowo zaburzona przez różnice w intensywności koloru.
W takich sytuacjach, jeżeli już chcemy dane przedstawiać za pomocą symboli, znacznie lepiej jest zamiast powiększać symbole zastosować zwielokrotnienie ich liczby. Gdyby użyć metafory, jeden symbol ludzika = 100 000 emigrantów, lewy ludzik zamieniłby się w 10 symboli, prawy ludzik w 20 symboli i zdecydowanie łatwiej byłoby zauważyć dwukrotną różnicę w liczbie symboli. Byłby to opis czytelniejszy i dokładniejszy niż użyty na tym wykresie.
Uwaga na osie
Częstą przyczyną pomyłek i utrudnień w odczytywaniu wartości z wykresu są niewłaściwe lub nieczytelne osie.
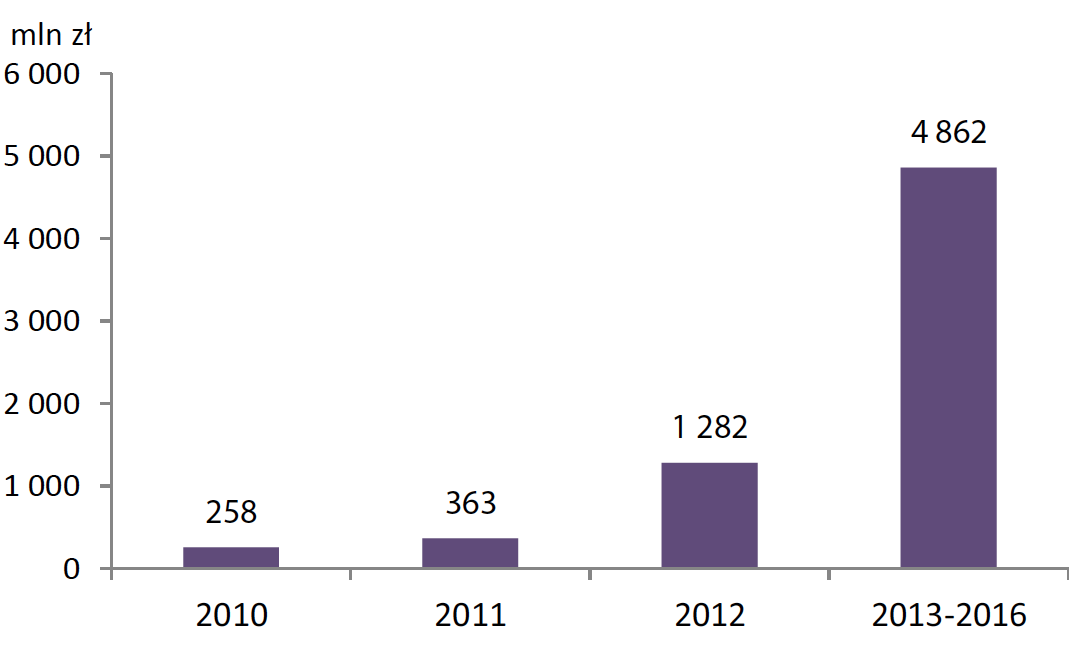
Interesujący przykład prezentowany jest poniżej. Pochodzi on z raportu Nauka w Polsce 2013 i przedstawia wydatki deklarowane na badania i rozwój. Wykres ten wygrał plebiscyt na najgorszą grafikę roku 2013 i również otwiera ten esej.
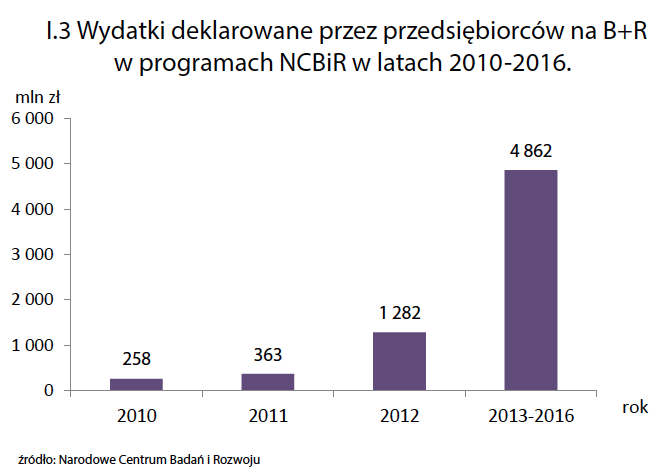
Wykres ten pokazuje znaczne wzrosty deklarowanych wydatków, co pozwala dalej mówić o rosnącej innowacyjności w przedsiębiorstwach
Rysunek 18: Wykres przedstawia deklarowane wydatki na badania i rozwój. Źródło: raport Nauka w Polsce 2013 opracowany przez Ministerstwo Nauki i Szkolnictwa Wyższego
Niestety, jeżeli przyjrzeć się bliżej, to okaże się, że ostatni słupek przedstawia wydatki zagregowanie z czterech lat (a dokładniej dotyczy planów na przyszłe cztery lata).
Jeżeli podzieli się te planowane wydatki przez cztery lata, otrzyma się kwotę 1215 mln złotych, czyli spadek o około 5% w stosunku do roku 2012. Ta “niewinna” agregacja na osi poziomej znacząco zmieniła postrzeganie prezentowanych danych.
Podobnie podejrzane są zestawienia, w których prezentowane wykresy mają różne zakresy wartości przedstawione na osiach. Przyjrzyjmy się poniższemu wykresowi z portalu Wyborcza.biz. Prezentuje on “zyskowność” ZUS i OFE na przestrzeni lat 2000–2011. Wrażenie, które można odnieść z tego wykresu, to wyższa zyskowność w ZUSie, w którym konsekwentnie wyniki są “nad kreską”
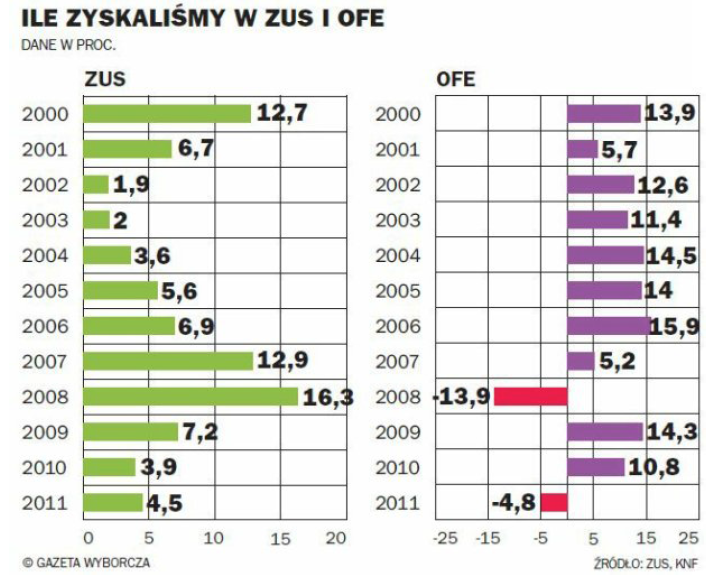
Jeżeli jednak przyjrzeć się bliżej tym wykresom, okaże się, że przedstawiane są różne zakresy na osiach poziomych. Na lewym wykresie przedstawiane są wartości w przedziale [0; 20], a na prawym [-25; 25]. Szerokość kratki na lewym wykresie odpowiada 5 punktom procentowym, a na prawym wykresie 10 punktom procentowym, co skutkuje tym, że “zysk” 15,9% OFE z roku 2006 wygląda na równie duży co “zysk” 6,9% ZUS w tym samym roku, choć dla OFE był ponad dwukrotnie większy.
Osoby, które nie zauważą różnic na osiach, pozostaną z przekonaniem o znacznie wyższej zyskowności ZUS. Nawet jeżeli zauważymy, że te osie się różnią, to trudno jest z tego wykresu odczytać, jaki był końcowy bilans ZUSu i OFE.
To zaskakujące, jak często można przeoczyć dziwne odwzorowania danych, jeżeli na prezentowanym wykresie nie zaznaczono osi. Przyjrzyjmy się wykresowi z artykułu Pensje nauczycieli rosną szybciej niż średnia krajowa [Portal praca.money.pl]
Rysunek 19: Wykres przedstawiający “zyski”z ZUS i OFE w ostatnich latach. Źródło: artykuł Który OFE zarobił dla klientów najwięcej? Zobacz pełne zestawienia z portalu “Wyborcza.biz”
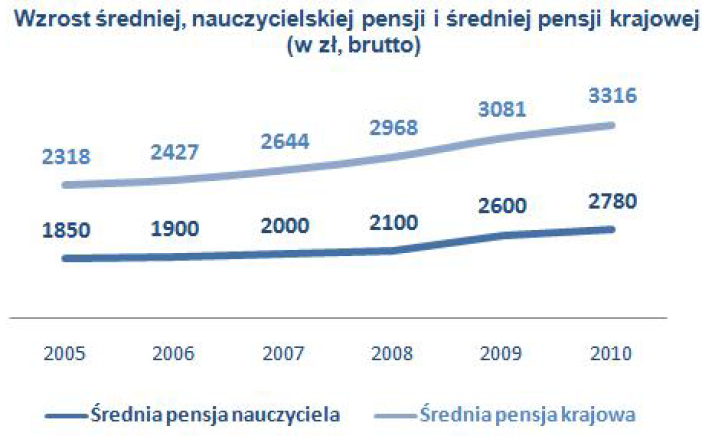
Rysunek 20: Wykres prezentujący średnią pensję nauczycieli i średnią krajową w ostatnich latach. Źródło: artykuł z portalu “
praca.money.pl”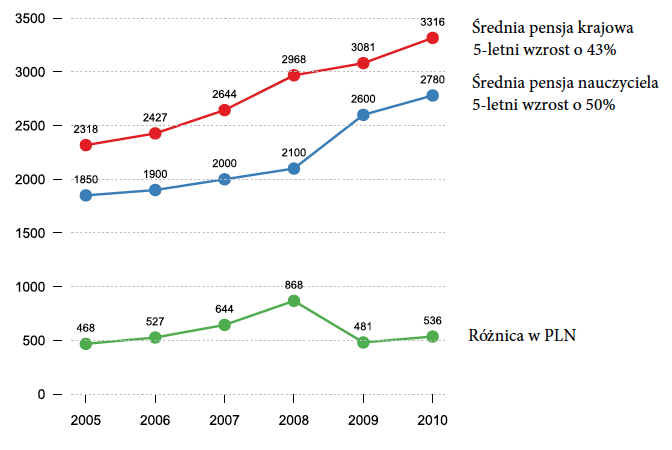
Wykres jest tak zaskakująco przygotowany, że wartość 2780, odpowiadająca średniej pensji nauczyciela w roku 2010, wygląda na niższą niż wartość 2318 odpowiadająca średniej krajowej pensji w roku 2005.
Rysunek 21: Wykres prezentujący średnią pensję nauczycieli i średnią krajową w ostatnich latach, przedstawiane są te same liczby, co na wykresie 20. Źródło: opracowanie własne
Mamy wrażenie, że średnia pensja nauczyciela nie dość, że się nie zmienia, to jeszcze jest znacznie poniżej średniej krajowej.
To nie ta historia
Największą konsternację budzą jednak wykresy, na których dane pokazują inną historię niż opisy tekstowe. Przyjrzyjmy się jeszcze jednemu wykresowi z raportu Nauka w Polsce 2013 opracowanego przez MNiSW. Wykres 22 przedstawia liczbę zgłoszonych wniosków o koordynację projektów, liczbę faktycznie koordynowanych projektów oraz współczynnik sukcesu. Polska jest zaliczona do grona najbardziej aktywnych krajów.
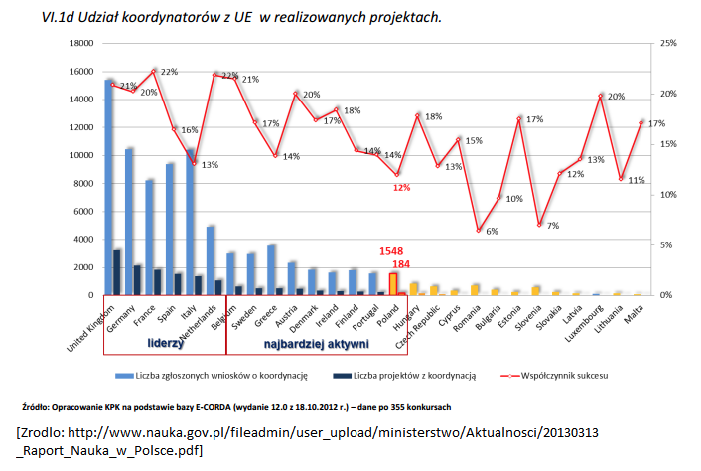
Spójrzmy jednak na liczby. Polska pod względem ludności jest szóstym krajem w Unii Europejskiej. Tymczasem pod względem liczby zgłoszonych wniosków jesteśmy zgodnie z tym wykresem na pozycji 15 na 27 wymienionych państw, czyli poniżej połowy (wyżej są kilkukrotnie mniejsze Irlandia czy Dania). Jeżeli brać pod uwagę współczynnik sukcesu, to Polska jest na 22 miejscu na 27 krajów, czyli poniżej 3/4 rankingu. Biorąc to pod uwagę, dziwić może określenie “najbardziej aktywni”. Bez szczegółowej analizy wykresu w pamięć zapadnie tylko komunikat “jesteśmy najbardziej aktywni i wspierają to liczby”, czyli komunikat w rzeczywistości niezgodny z przedstawianymi liczbami.
Rysunek 22: Wykres z raportu Nauka w Polsce 2013 opracowanego przez Ministerstwo Nauki i Szkolnictwa Wyższego

Kolejny przykład przedstawia rysunek 23. Pokazuje on, jaka część spośród wszystkich uprawnionych do głosowania wyborców głosowała na partie Prawo i Sprawiedliwość lub Kukiz'15. Historia, którą ten wykres miał prawdopodobnie komunikować to, że te dwie partie nie mają mandatu większości wyborców. Jednak ta historia nie została właściwie przedstawiona.
Gdyby chcieć ją poprawnie przedstawić, to należałoby pokazać wszystkich wyborców (ponad 30 milionów) za pomocą pola kwadratu, koła, liczebności ikon/symboli zgodnie z techniką ISOTYPE lub jeszcze w inny sposób. Następnie należałoby zaznaczyć jaka część z wyborców wzięła udział w wyborach (frekwencja wyniosła 50,92 procent). Z tych którzy wzięli udział, ilu głosowało na PiS lub Kukiza. Jeżeli dane przedstawiane byłyby za pomocą pól, lub liczby symboli, to należałoby zatroszczyć się by proporcje pól lub symboli odpowiadały danym. Na załączonej grafice tak nie jest. Proporcje pól na wykresie to 1:18:313 ale proporcje wynikające z liczb to 1:4:18.
Dodatkowo zagnieżdżone koła sugerują, że jedna grupa jest częścią innej. Ale przecież w tej historii tak nie jest. Wyborcy Kukiza nie są podzbiorem wyborców partii PiS, a ci z kolei nie są podzbiorem osób, które nie głosowali.
A może przymknąć na to oko?
W tym miejscu należy zadać sobie pytanie, czy takie szczegóły mają znaczenie? Czy należy się przejmować tym, że ministerialne wykresy potrafią dwukrotnie zniekształcić prezentowane dane? Czy warto walczyć o poprawne wykresy pokazujące dokładnie to, co jest w danych i nic więcej? Bez źle rozumianego marketingu i zbędnych upiększeń.
Myślę, że warto. Nasza percepcja i pamięć płata zaskakujące figle, upraszczając i wybiórczo traktując komunikaty, które zapamięta. Jeżeli chcemy, by w naszej pamięci osiadały prawdziwe historie, prawdziwe relacje i związki, nie powinniśmy pozwalać na nawet najmniejsze błędy, mogące spowodować, że zapamiętamy niepoprawnie fakty, reguły czy informacje. Celem grafiki statystycznej jest koniec końców ułatwienie zrozumienia zależności prezentowanych przez liczby, a nie utrudnienie czy uniemożliwienie odczytania tej zależności.