
Epilog
Beta i Bit wrócili do swoich czasów tylko dlatego, że odkryli reguły rządzące wehikułem czasu. Zauważyli i potrafili wykorzystać informacje o tym, jak rok, w którym się pojawili, zależy od liczby wpisanej do sterownika wehikułu. Zdolność dostrzegania takich związków przydaje się nie tylko, gdy planujemy „włam” do pracowni szalonego matematyka. Świat wokół nas jest najeżony zależnościami. Umiejętność ich zauważania i wykorzystywania okazuje się przydatna w różnych sytuacjach.
Przydała się do wyjaśnienia katastrofy promu Challenger, która miała miejsce w 1986 roku. W 45 sekundzie po starcie wahadłowca oczom obserwatorów ukazał się jęzor ognia, który natychmiast doprowadził do rozpadu promu i katastrofy, w której zginęła cała załoga. Przyszłość NASA stanęła pod znakiem zapytania. Specjalna komisja powołana do wyjaśnienia przyczyn katastrofy długo szukała jakichkolwiek wskazówek. W pracach komisji brał udział Richard Feynman, fizyk, późniejszy noblista. Zauważył on, że temperatura otoczenia zmniejsza sprężystość gumowych pierścieni uszczelniających silnik rakiety. A mniejsza sprężystość przekłada się na większą awaryjność. Już poniżej temperatury 18 stopni Celsjusza pojawiały się problemy z pierścieniami uszczelniającymi, które występowały tym częściej, im niższa była temperatura. Przy 10 stopniach Celsjusza sprężystość okazała się niewystarczająca. A w nocy poprzedzającej start promu temperatura spadła poniżej zera.
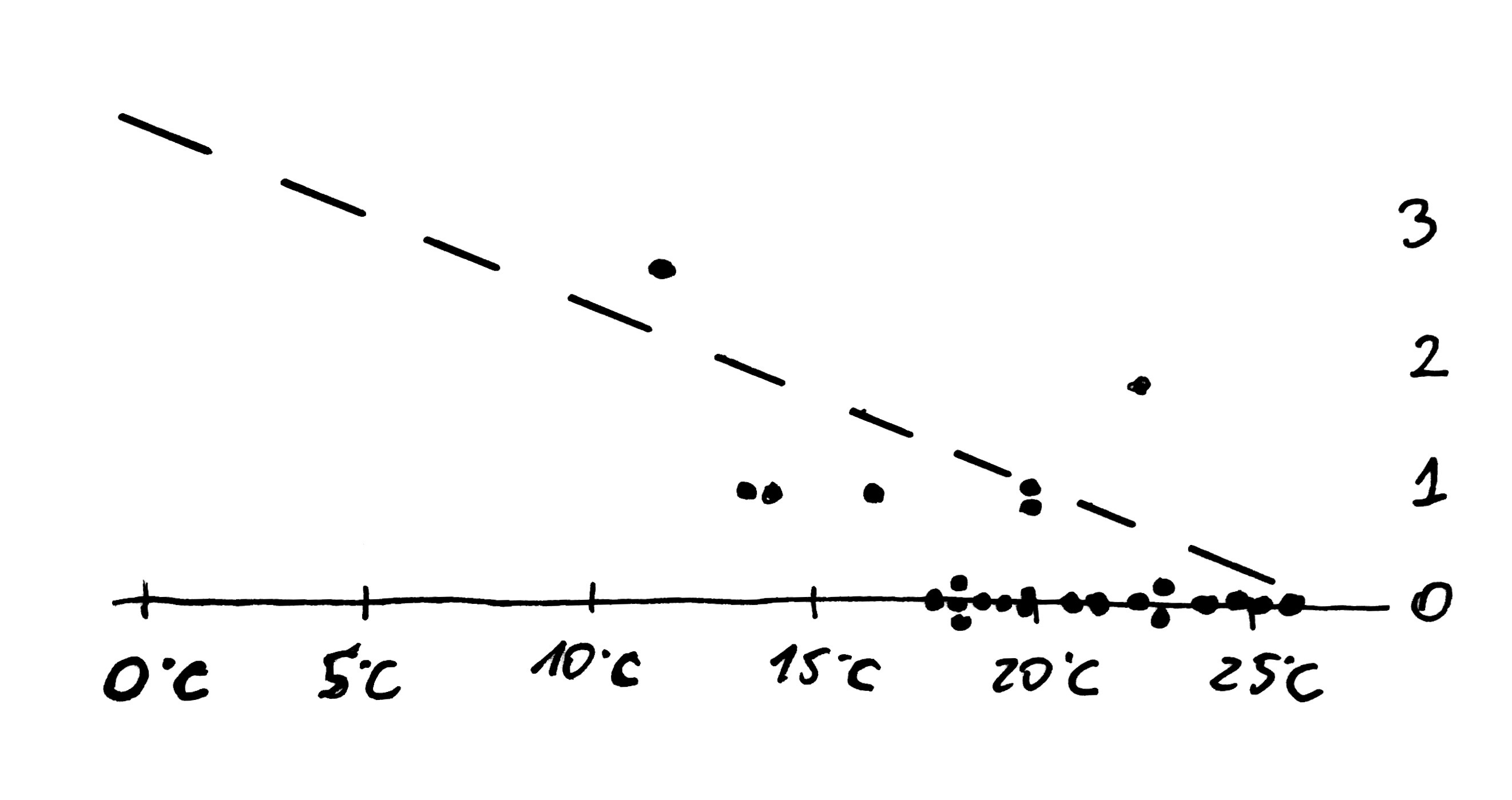
Poniższy wykres za pomocą kropek przedstawia wyniki wstępnych pomiarów zależności liczby uszkodzeń od temperatury. Wszystkie pomiary zbierane były w temperaturach od 10 do 25 stopni Celsjusza – w tym przedziale widać, że im zimniej, tym więcej uszkodzeń. Czy znając tę prawidłowość, można było przewidzieć poważną awarię, która wystąpiła przy zerowej temperaturze?
Jedna z metod szukania zależności pomiędzy zmiennymi to regresja. Skąd ta nazwa? Otóż ma ona bardzo ciekawe pochodzenie. W 1886 roku sir Francis Galton badał zależność wzrostu dorosłych synów od wzrostu ich rodziców. Zauważył, że synowie wysokich rodziców są zazwyczaj wysocy, ale wcale nie tak wysocy jak ich rodzice. Oczywiście niektóre dzieci były bardzo wysokie, czasem wyższe od rodziców, ale gdy badało się średnie, to wzrost dzieci wypadał gdzieś pomiędzy wzrostem rodziców a średnim wzrostem wszystkich dzieci. Tę tendencję Galton określił terminem „powrotu do przeciętności” (regression toward mediocrity).
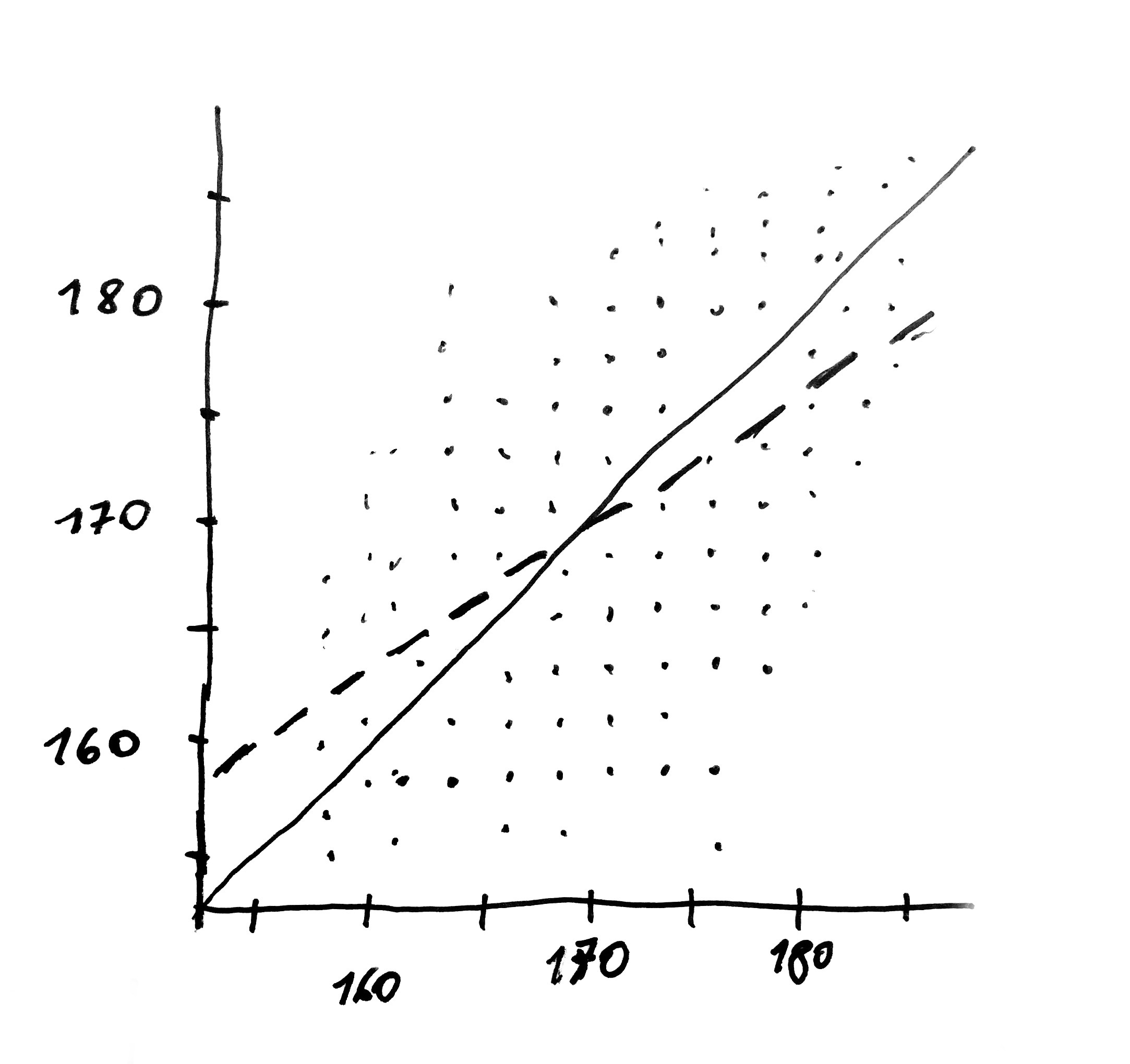
Poniższy diagram ilustruje badania Galtona. Przebadano około 1000 osób. Za pomocą punktów na osi OX przedstawiono średni ważony wzrost rodziców, a na osi OY – wzrost dzieci. Linią ciągłą oznaczono zależność odpowiadającą równości wzrostu dzieci i rodziców. Linia przerywana to z kolei zależność widoczna w danych. Można zauważyć, że średni wzrost dzieci jest bliższy linii poziomej. W przeciwieństwie do par liczb zebranych przez Betę i Bita punkty pomiarowe nie układają się idealnie w linię prostą. Poszukiwana linia opisująca zależność to linia, która jest możliwie najbliżej wszystkich punktów.
Ktoś może zapytać, jaka jest wartość takich badań. Co ciekawego może dać wiedza o tym, że średni wzrost dziecka jest w pewnej części zależny od wzrostu rodziców, a w pewnej części nie? Okazuje się, że ta sama technika regresji przyczyniła się do ogromnego postępu w rolnictwie i hodowli trzody chlewnej. Informacja o tym, jaka część mleczności krowy jest dziedziczona od byka, jaka od krowy, a jaka nie jest dziedziczona przydaje się do oceny wartości hodowlanej zwierzęcia. Dziś badania wartości hodowlanej prowadzone są na dużą skalę i uwzględniają często bardzo złożony rodowód zwierząt. Doprowadziło to do znacznego zwiększenia mleczności krów. Szacuje się, że w krajach rozwiniętych przez ostatnie 50 lat uległa ona potrojeniu! Podstawą tych badań jest nic innego jak regresja.
Zapytacie pewnie, czy regresja może się przydać w codziennym życiu. Otóż tak i jest na to wiele dowodów. Załóżmy, że chcemy kupić lub sprzedać używany samochód, mieszkanie lub telefon. Albo zastanawiamy się, ile może kosztować pięcioletni volkswagen passat o przeciętnym wyposażeniu. Na portalach z używanymi samochodami znajdziemy setki ofert sprzedaży. Możemy więc pobrać te dane i poszukać zależności między wiekiem auta a jego ceną. Co się okazuje? Jeżeli zestawimy logarytm ceny z wiekiem auta, to naszym oczom ukaże się piękna liniowa zależność. Skąd ten logarytm? Otóż używane auta tracą na wartości co roku mniej więcej stały procent ceny, około 15% (dokładna wartość zależy od marki i wyposażenia). Po roku samochód traci więc na wartości 15%, po dwóch latach już 27,8% (dlaczego? kłaniają się procenty złożone), po trzech latach 38,6% ceny i tak dalej. Gdy jednak cenę się zlogarytmuje, to procent składany zamienia się w liniową zależność, pozwalającą na proste oszacowanie ceny używanych aut.
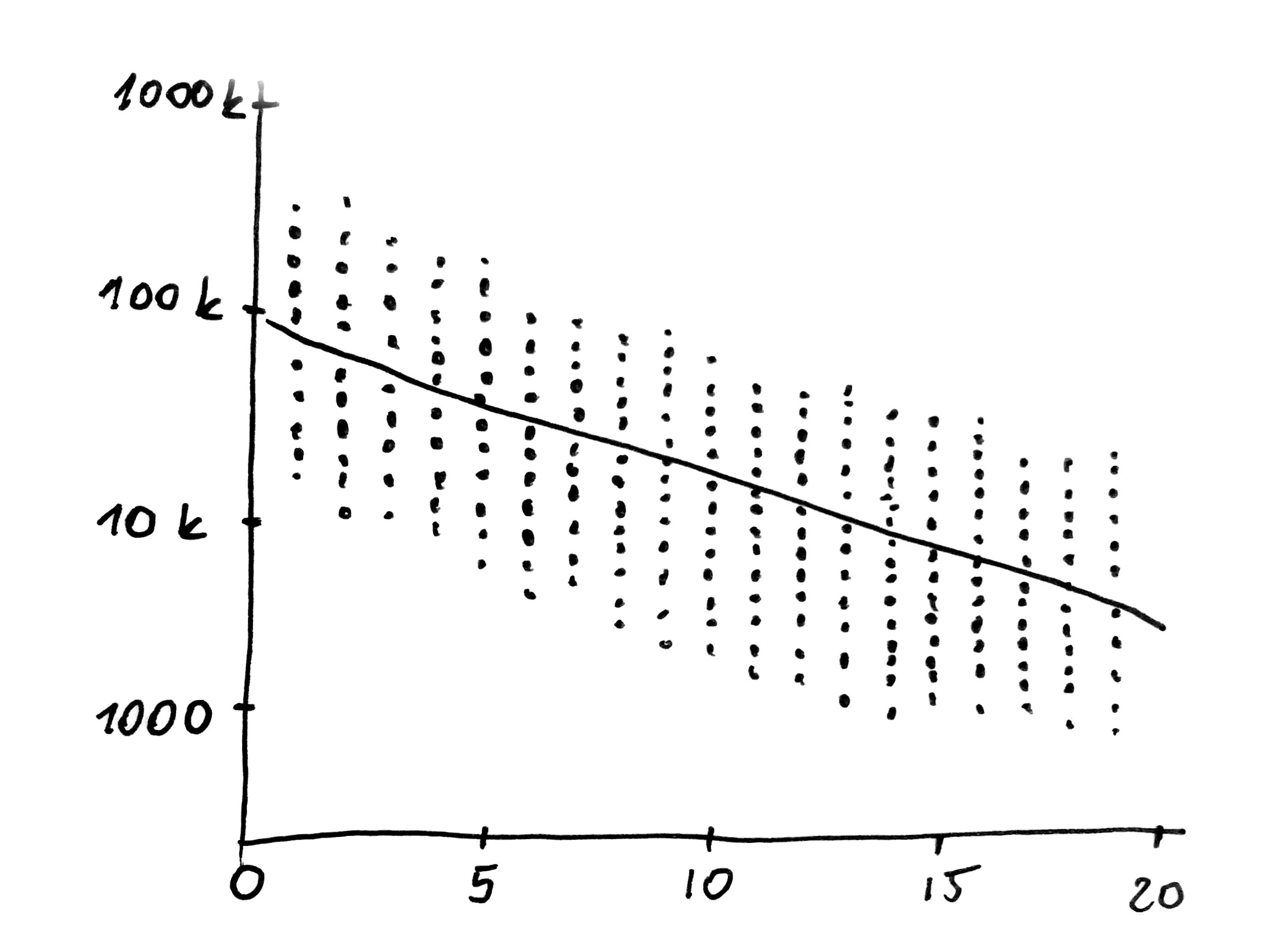
Poniższy diagram przedstawia zależność pomiędzy ceną na skali wykładniczej (na osi OY) a wiekiem auta w latach (na osi OX). Dane pobrano z portalu OTOMOTO.
Jednak nie każda zależność jest liniowa. Pozostańmy przy temacie używanych samochodów. Okazuje się, że bardzo interesująco wygląda związek pomiędzy przebiegiem auta a jego wiekiem.
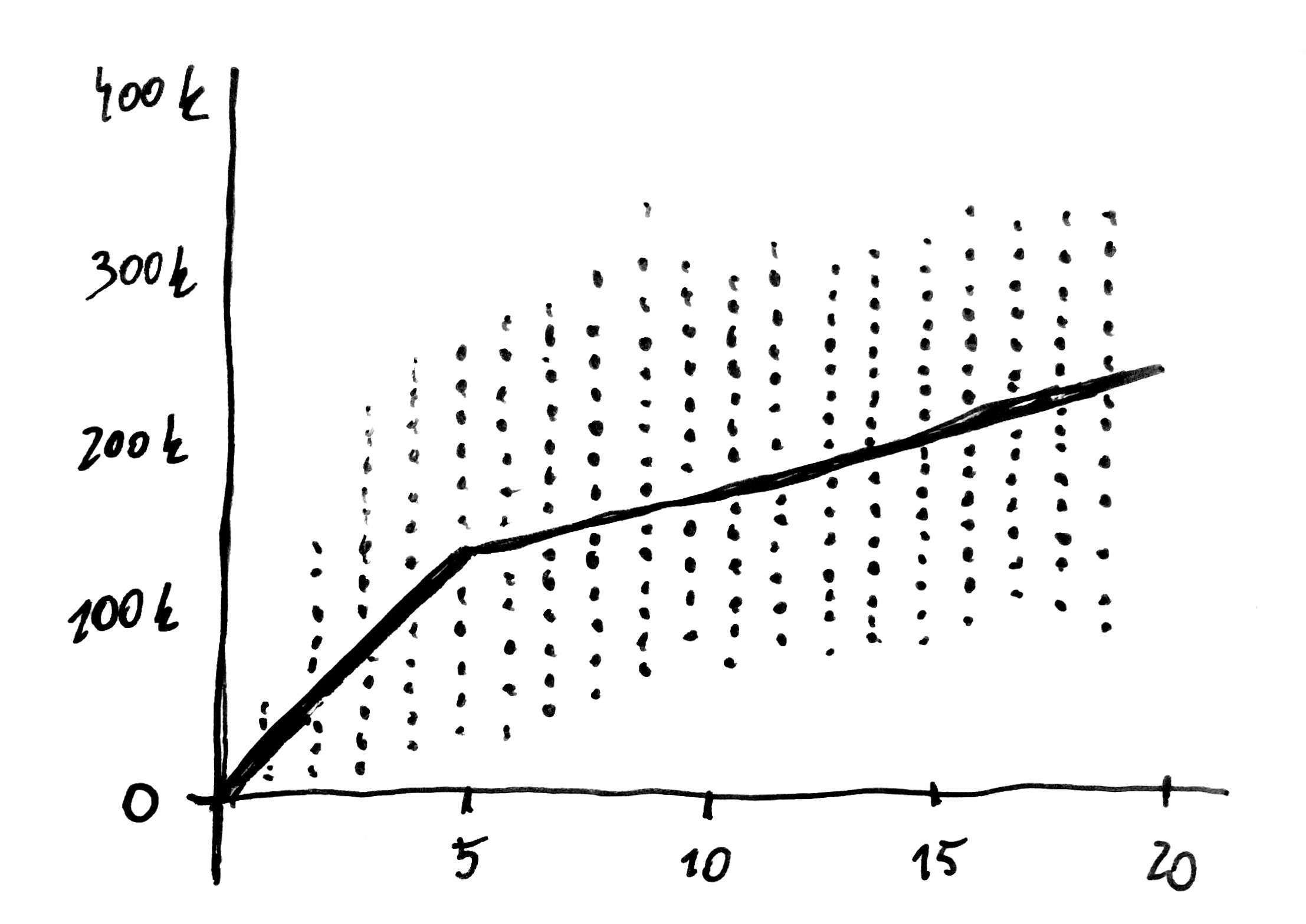
Wydawać by się mogło, że przebieg powinien zwiększać się proporcjonalnie do wieku auta. Jeżeli w jednym roku przejeżdża się jakąś liczbę kilometrów, to przez dwa lata przejeżdża się dystans mniej więcej dwukrotnie dłuższy. Co jednak ciekawe, gdy analizuje się wykres przedstawiający przebieg samochodu w zależności od jego wieku, to zauważyć można inną zależność dla aut, których wiek nie przekroczył pięciu lat, i inną dla aut starszych. Nowsze samochody zwiększają przebieg w tempie około 20-25 tys. kilometrów na rok, ale już po pięciu latach roczny przebieg zaczyna wzrastać jedynie o 10-15 tys. kilometrów. Taka zależność może być wynikiem innych zachowań właścicieli aut starszych (najwięcej jeżdżą przedstawiciele handlowi, najczęściej korzystający z nowych samochodów, które później są sprzedawane) lub innych zachowań sprzedawców (auta o dużym przebiegu mają zmniejszany przebieg – w przypadku starszych samochodów rzadko prowadzi się książkę serwisową, więc nie ma dowodów tego oszustwa).
Doszukując się zależności pomiędzy zmiennymi, należy być ostrożnym z wysuwaniem wniosków. To, że dwie zmienne są zależne, nie oznacza wcale, że jedna stanowi przyczynę drugiej. Gdy przeanalizuje się dane dla różnych wsi o liczbie narodzin dzieci i liczbie bocianich gniazd, okazuje się, że pomiędzy tymi wartościami występuje bardzo silny związek. Im więcej bocianich gniazd, tym więcej narodzin dzieci! Nie dowodzi to jednak, że bociany przynoszą dzieci. Czego więc dowodzi? Im większa wieś, tym więcej w niej domów, tym więcej dachów, tym więcej słupów i innych miejsc, gdzie bociany mogą założyć gniazdo. Więcej domów i więcej ludzi to oczywiście też więcej dzieci. Dlatego liczby dzieci i bocianów są zależne, zależą bowiem razem od jeszcze innej zmiennej – liczby domostw.