
Ludzki mózg jest często porównywany do superkomputera. Można to określenie spotkać często, głównie dlatego, że jesteśmy łasi na takie pochlebstwa. Któż by nie chciał mieć czegoś “super” w głowie? Nie ma wątpliwości, że mózg jest wyjątkowy, więc określenie “super” jest jak najbardziej na miejscu. Problem z tym porównaniem leży w określeniu “komputer”. Musimy bowiem wiedzieć, że sposób działania mózgu w niczym nie przypomina sposobu działania komputera.
Komputer to bardzo rozbudowany kalkulator, wykonujący szybko operacje logiczne i arytmetyczne na liczbach. Nasz mózg jednak nie pracuje na liczbach w sposób naturalny. Od przedszkola ćwiczymy go by opanować coraz to bardziej złożone operacje matematyczne, zaczynając od liczenia, dodawania, odejmowania, przez tabliczkę mnożenia, funkcje trygonometryczne, czasem rachunek różniczkowo-całkowy. Te operacje nie są dla mózgu naturalne, aby je opanować potrzebujemy wieloletniego treningu. Im dłużej ćwiczymy, tym bardziej zmienia się sposób, w jaki myślimy o liczbach, prawdopodobieństwie, zależnościach pomiędzy cechami. Oznacza to jednak, że ludzie bardzo się różnią, jeżeli chodzi o biegłość w operowaniu liczbami i zależnościami. Im szersze jest grono planowanych odbiorców, tym bardziej należy uważać na potencjalne problemy ze zrozumieniem zależności pomiędzy liczbami.
Dobra grafika statystyczna powinna pokazywać informację zawartą w danych liczbowych. Powinna to robić w taki sposób, by łatwo było odczytać i zrozumieć związek pomiędzy informacją a danymi. Obrazować, jak duże są pewne wielkości, jak ryzykowne są pewne rozwiązania, jak wyglądają zależności pomiędzy zjawiskami. Aby przekaz był zgodny z zamierzeniami, musimy być świadomi sposobu, w jaki nasz mózg postrzega liczby i zależności, w jaki sposób myśli o danych i w jakich sytuacjach postrzeganie liczb lub zależności może być zniekształcone.
Poniżej w czterech podpunktach pokażemy: jakie trudności są związane z percepcją dużych liczb, rzadkich zdarzeń, przypadkowości oraz zależności. Wiedząc o tych trudnościach, możemy lepiej zaprojektować wizualizację danych, aby ułatwić odbiorcy poprawne zrozumienie informacji.
Komunikacja dotycząca zależności pomiędzy liczbami bardziej przypomina przeprawę statku przez najeżone rafami wody, niż przesył danych z komputera do komputera. Chcemy pływać po tych wodach bezpiecznie? Zobaczmy, gdzie znajdują się największe przeszkody. Poniżej na przykładach pokażemy, jak trudno jest myśleć o dużych liczbach, małych prawdopodobieństwach i przypadkowych zależnościach. Pokażemy też, jak za pomocą prostych sztuczek ułatwić ludzkiej percepcji zrozumienie tych często abstrakcyjnych pojęć.
Zrozumienie, w jaki sposób ludzie myślą o liczbach i zależnościach jest kluczowe dla dobrej wizualizacji danych. Koniec końców, w prezentacji danych wcale nie chodzi o to, by pokazać dane, ale by dane były zaprezentowane w sposób umożliwiający zrozumienie informacji, którą przedstawiają.
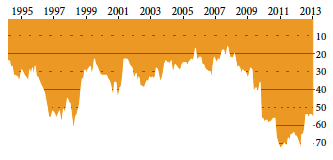 Rysunek 1: Pozycja Polski w rankingu FIFA w latach 1995-2013. Przedstawiana informacja to ostatnio gorsze wyniki kadry narodowej w piłce nożnej. Komunikat jest prezentowany za pomocą głębokości zanurzenia pomarańczowych słupków, oznaczających pozycję w międzynarodowym rankingu krajów w piłce nożnej FIFA. Źródło: opracowanie własne
Rysunek 1: Pozycja Polski w rankingu FIFA w latach 1995-2013. Przedstawiana informacja to ostatnio gorsze wyniki kadry narodowej w piłce nożnej. Komunikat jest prezentowany za pomocą głębokości zanurzenia pomarańczowych słupków, oznaczających pozycję w międzynarodowym rankingu krajów w piłce nożnej FIFA. Źródło: opracowanie własne
Za duża, żeby zrozumieć
Okazuje się, że większości osób operacje na bardzo dużych lub bardzo małych liczbach sprawiają znaczne kłopoty. Spora część dziennikarzy ma problem z rozróżnieniem miliarda od biliona co widać po bezrefleksyjnym i błędnym tłumaczeniu angielskiego billion na polskie słowo bilion. Dla większości ludzi, z wyjątkiem być może fizyków, miliard czegokolwiek jest pojęciem czysto abstrakcyjnym. Podobnie abstrakcyjnym, jak dla mieszkańców plemienia Pirahã liczba dziesięć. Fizycy, przechodząc od skali kosmologicznej do subatomowej, przeskakując przez dwadzieścia rzędów wielkości, nabierają pewnych intuicji, obcych jednak większości ludzi.
Z drugiej strony, żyjąc w dzisiejszym świecie, na co dzień obcujemy z dyskami o pojemności terabajtów, oglądamy filmy zapisane jako pliki o objętości gigabajtów, słyszymy o bilionowych zmianach w globalnych gospodarkach. Słysząc o budżetach państw czy aferach korupcyjnych, słyszymy czasem o milionowych lub miliardowych kwotach. Skoro tak duże liczby są wszędzie wokół, można by przypuszczać, że je rozumiemy.
Nic bardziej mylnego!
Przeprowadźmy prosty eksperyment. Zapytaj, drogi Czytelniku, dowolną osobę o to, czy słowo biliard jest odpowiednikiem przedrostka giga czy tera W grupie osób o wykształceniu humanistycznym rozkład odpowiedzi pomiędzy giga a tera jest bliski proporcjom pół na pół. W grupie osób o ścisłym wykształceniu opcję tera wybiera około trzech czwartych ankietowanych, co nie jest dobrym wynikiem, ponieważ biliard odpowiada tak naprawdę przedrostkowi peta.
No dobrze, to pytanie można uznać za podchwytliwe. W końcu żadna z sugerowanych opcji nie była prawdziwa, więc ktoś, kto trudno znosi uświadomienie sobie swojej niewiedzy może argumentować, że sugerowanie złych odpowiedzi wpłynęło na pomyłkę. Zadajmy więc pytanie bez żadnych kruczków.
Co więcej, takie, na które teoretycznie każdy z nas powinien znać odpowiedź.
Ile wynosi dług publiczny Polski?
Pytanie zadane w tej postaci nie proste, ponieważ ten dług nieustannie się zmienia (czytaj rośnie). Ale przyjmijmy, że interesuje nas wartość długu na dzień 11 października 2013. Dla większości osób “ta liczba” jest tak niewyobrażalna, że nawet, jeżeli czytali o niej rano, to jej nie zapamiętali. Odpowiedzią poprawną 11 października 2013 roku o 15:27 było 937 457 092 004 PLN. Ta liczba ma 12 cyfr, ale nawet jej zapamiętanie, chociażby z dokładnością do pierwszych dwóch cyfr, jest trudne. 940 miliardów. Zdecydowana większość z nas nie doświadczyła nigdy obserwacji miliarda czegokolwiek, 940 miliardów to tak abstrakcyjna liczba, że nie sposób jej zapamiętać
Z kilku osób, które akurat spotkałem na kawie i które zapytałem o wielkość długu publicznego, tylko jedna podała odpowiedź nie różniącą się od prawdziwej o więcej niż rząd wielkości (to znaczy pozostałe odpowiedzi były albo ponad 10 razy niższe, albo 10 razy wyższe niż prawdziwa wartość). Osoba, która była blisko poprawnej odpowiedzi, oczywiście nie pamiętała wartość długu, ale miała orientacyjne wyobrażenie, ile wynosi wartość długu na jednego mieszkańca. Przyjęła, że wartość długu to około 20 tysięcy na mieszkańca, a w Polsce żyje około 38 milionów Polaków. Te dwie liczby można dosyć łatwo wymnożyć w pamięci i otrzymać 760 miliardów. Ta ocena była możliwa tylko dlatego, że jesteśmy w stanie sobie wyobrazić, ile to jest 20 tysięcy. To kwota, z którą spotykamy się, kupując samochód, rozliczając roczne podatki i jest dla nas bardziej przystępna niż miliardy czy biliony.
Wielkość 940 miliardów jest poza zakresem zrozumienia wielu osób. Jak to możliwe, że dziennikarz, tłumacząc artykuł z angielskojęzycznego źródła, myli angielskie billion z polskim bilionem? Zawyża opisywaną wartość tysiąckrotnie i nawet tego nie zauważa? Z pewnością tysiąc jabłek i jedno jabłko to dwie różne wielkości i oczyma wyobraźni widzimy o ile się różnią. Ale bilion a biliard kilometrów? Czy słońce jest więcej czy mniej niż bilion kilometrów od Ziemi?
Czy jesteśmy bezbronni w obliczu biliardów, czy też jest sposób, by oswajać duże liczby? Są sposoby, dwa najczęściej stosowane zostały już wymienione.
Pierwszy to odnoszenie się do jednostek, które jesteśmy w stanie odtworzyć w pamięci. Z uwagi na rewolucję komputerową można się odwoływać do przedrostków kilo, mega, giga i tera i, przynajmniej wśród osób często korzystających z komputera, mamy szansę na poprawne skojarzenia. Mówienie o terazłotych długu publicznego nie jest zbyt powszechne, ale wielu osobom znacznie bardziej zapada w pamięć i pozwala na znacznie łatwiejsze operacje na tej kwocie niż mówienie o bilionie złotych.
Drugi sposób to rozkład dużej liczby na iloczyn dwóch lub trzech mniejszych. Taka operacja nazywa się faktoryzacją i w ogólności jest to trudne zagadnienie, ale przy przyzwoleniu na ograniczoną dokładność faktoryzację dużych liczb można wykonać w miarę łatwo. Świetnym tego przykładem jest projekt Fundacji Forum Obywatelskiego Rozwoju Rachunek od państwa, przedstawiający wydatki publiczne Polski w formie rachunku dla obywatela. Rachunek, który rozbija roczne wydatki państwa, wyrażane w miliardach złotych, na głowę mieszkańca, przez co znów mamy do czynienia z liczbami, które możemy sobie wyobrazić. Prosty zabieg pozwala na sprowadzenie olbrzymich sum, do takich, które możemy zrozumieć i odnieść do codziennego życia. Przykładowo rocznie średnio płacimy na emerytury ZUS 2,4 tysiąca złotych, to duża część z 18 tysięcy, czyli całej kwoty rachunku. Prawie 4,5 tysiąca złotych rocznie na obsługę samych emerytur i rent? Z tej perspektywy łatwiej ocenić, czy to dużo, czy mało.
Z szacowaniem dużych wielkości związane jest jeszcze jedno ciekawe zjawisko określane jako “kotwiczenie”, które jest częstym źródłem zniekształceń dla naszych oszacowań. O co w nim chodzi?
Przeprowadźmy wirtualny eksperyment. Przypuśćmy, że zadajemy grupie osób pytanie: Jak uważasz, czy dług publiczny jest wyższy, czy niższy niż 100 miliardów złotych, a właściwie, jak uważasz, ile on wynosi? Zbieramy odpowiedzi, liczymy średnią oszacowań. Jak uważacie, czy będzie się ona różniła od średniej wyliczonej z odpowiedzi na pytanie: Jak uważasz, czy dług publiczny jest wyższy, czy niższy niż 1 000 miliardów złotych, a właściwie jak uważasz, ile on wynosi?
Najprawdopodobniej w obu tych eksperymentach otrzymalibyśmy bardzo różne średnie. W książce [Daniel Kahneman. Thinking, Fast and Slow Farrar, Straus and Giroux, 2011] Daniel Kahneman, laureat nagrody Nobla w dziedzinie ekonomii za prace nad decyzjami podejmowanymi w warunkach niepewności, opisuje podobny, tym razem przeprowadzony naprawdę eksperyment. W oryginalnym badaniu pytano: Czy najwyższa sekwoja ma 365 m? Właściwie ile metrów może mieć najwyższa sekwoja? Na tak zadane pytanie średnia z odpowiedzi wynosiła 257 m, ale już gdy w pierwszej części pytania zasugerowano 55 m, to średnia z odpowiedzi spadła do 87 m.
 Rysunek 2: Rachunek od państwa 2012, opracowany przez Fundację Forum Obywatelskiego Rozwoju. Źródło:
http://www.dlugpubliczny.org.pl/
Rysunek 2: Rachunek od państwa 2012, opracowany przez Fundację Forum Obywatelskiego Rozwoju. Źródło:
http://www.dlugpubliczny.org.pl/
Zaskakujące? Zaproponowanie punktu odniesienia znacząco zmienia wartość szacunków. Czy zjawisko zakotwiczenia ma związek z wizualizacją danych? Oczywiście. Każdy element wykresu może pełnić rolę takiej kotwicy. Jeżeli w tle umieścimy zdjęcie wieży Eiffela, natychmiast wzrośnie średnie wyobrażenie dotyczące wielkości prezentowanych liczb, ponieważ w kontekście pojawi się kotwica mówiąca “duże”. Dla jednych jest to argument, aby unikać wszelkich zbędnych elementów i nie obciążać percepcji przy czytaniu wykresu, dla innych jest to sugestia, by dodawać jak najwięcej zbędnych elementów tak, by percepcję odbiorcy wykrzywić w pożądany sposób.
Jak długo trwa takie zakotwiczenie? Czy na odpowiedź wpływa tylko kilkusekundowy kontekst? Okazuje się, że w wielu przypadkach na nasze oceny i zachowania mogą mieć wpływ zdarzenia, obrazy, komunikaty, które otrzymaliśmy nawet kilkanaście minut wcześniej. W książce [Malcolm Gladwell. Blink: The Power of Thinking Without Thinking Back Bay Books, 2005] znaleźć można kilka takich przykładów podanych w formie ciekawych anegdotek. Jedna z nich opisuje doświadczenie, w którym badani musieli w myśli odpowiadać na pytania. Pytania były tak dobrane, by odpowiedzi dotyczyły słów związanych z cierpliwością (jedna grupa) lub ze zniecierpliwieniem (druga grupa). Okazuje się, że to zadanie wpływa na zachowania badanych nawet do kilkunastu minut po zakotwiczeniu. Osoby, które myślały o słowach związanych z cierpliwością, nawet po kilkunastu minutach zachowywały się bardziej cierpliwie.
Dziękuję za odpowiedź, ale nie o to pytałem
Jak widzieliśmy, dla wielu z nas problemem może być operowanie na dużych liczbach. Podobne problemy dotyczą operowania na prawdopodobieństwach, szczególnie tych małych. O ile wyobrażamy sobie, co oznacza prawdopodobieństwo 1/2 (rzut monetą) lub 1/6 (rzut kostką do gry), to w przypadku mniejszych prawdopodobieństw jesteśmy bezbronni. Wyjątkiem są być może hazardziści, ale nie ci, co grają w loterie o szansie wygranej porównywalnej ze zderzeniem z meteorytem.
Przykładów, ilustrujących, że nasz umysł słabo sobie radzi z szacowaniem dużych wielkości jest wiele. A co z małymi liczbami? Na przykład szacunkami prawdopodobieństw rzadkich zdarzeń? Czy potrafimy wyobrazić sobie i operować na częstościach lub ryzykach występowania zdarzeń rzadkich?
Niestety nie. Małe prawdopodobieństwa to kolejna rafa na szerokich wodach percepcji liczb i zależności.
Problem percepcji małych prawdopodobieństw przedstawimy na przykładzie pytania dotyczącego częstości różnych przyczyn zgonów w Polsce.
Czy w roku 2010 więcej osób umarło z powodu:
udanych prób samobójczych,
wypadku samochodowego,
grypy lub zapalenia płuc?
W uważnym czytelniku, już samo pytanie wzbudzi czujność. Skoro pyta, odpowiedź może nie być intuicyjna. Gdyby wyeliminować składową wynikającą z podejrzliwości, szacowanie tych prawdopodobieństw odbywałoby się zgodnie z algorytmem: Czy znamy dokładne wartości? Może czytaliśmy ostatnio rocznik statystyczny z roku 2010, być może słyszeliśmy już tę zagadkę, może znamy dokładną odpowiedź? Jeżeli nie znamy dokładnej odpowiedzi, to zaczynamy ją szacować na bazie dostępnych informacji, w tym informacji o tym, jak często słyszeliśmy lub czytaliśmy o śmierci z poszczególnych powodów. Jeżeli nie czytamy roczników statystycznych, to najczęściej o zgonach dowiadujemy się z internetu, prasy, radia lub telewizji. O zgonach spowodowanych zapaleniem płuc w mediach się nie mówi, nie jest to ciekawy temat. O zgonach spowodowanych grypą mówi się przy okazji epidemii grypy, ale w poprzednim roku nie miała miejsca żadna medialna epidemia. W przypadku prób samobójczych zakończonych zgonem dowiadujemy się o nich najczęściej, jeżeli ofiarą jest znana osoba, polityk, aktor, celebryta. Najczęściej w mediach słyszy się o zgonach spowodowanych wypadkami samochodowymi. Nawet jeżeli nie oglądamy telewizji, to informacje o zgonach i wypadkach spotkać można w oznaczeniach czarnych punktów na drodze, a więc miejsc, gdzie wydarzyło się szczególnie dużo wypadków.
Najbardziej naturalna wydaje się odpowiedź “wypadek samochodowy”, ponieważ na bazie trafiających do nas komunikatów te przyczyny wydają się być najczęstsze.
Tymczasem, zgodnie z danymi [World Life Expectancy. Poland total deaths by cause, 2010] w roku 2010 w Polsce samobójstwo było przyczyną 6 479 zgonów (2,2% wszystkich zgonów), podczas gdy wypadek drogowy był przyczyną 6 224 zgonów (2,1% wszystkich zgonów), a grypa lub zapalenie płuc było przyczyną 10 033 zgonów (3,42% wszystkich zgonów). Tak więc najczęstszą z tych trzech przyczyn jest najmniej medialna śmierć z powodu grypy lub zapalenia płuc, a najrzadszą jest ta najczęściej w mediach przedstawiana, a więc śmierć spowodowana wypadkami samochodowymi.

Osoby szacujące częstości poszczególnych przyczyn śmierci znacząco przeszacowują częstości zgonów, o których często się mówi w mediach, a niedoszacowują częstości tych zgonów, o których w mediach się nie mówi. Takie niedoszacowywanie lub przeszacowywanie częstości nie dotyczy wyłącznie pytań związanych z przyczynami śmierci, ale jest bardzo częstym zjawiskiem, występującym w przypadku szacowania wartości spółek giełdowych, oceny działalności polityków, oceny przestępczości i wielu innych obszarów.
W ogólności takie zniekształcenie percepcji jest związane ze sposobem skojarzeniowego szukania odpowiedzi na trudne pytania. Z punktu widzenia wizualizacji danych najbardziej przydatny opis tego zjawiska jest przedstawiony w książce [Daniel Kahneman. Thinking, Fast and Slow. Farrar, Straus and Giroux, 2011] Autor, Daniel Kahneman, opisuje dwa modelowe tryby pracy naszej percepcji, nazwane przez niego System 1 i System 2. Na nasze potrzeby użyjemy łatwiejszych do zapamiętania nazw “moduł kreatywny” i “moduł krytyczny”. Gdy napotkamy pytanie, takie jak na przykład dotyczące częstości przyczyn zgonów, moduł kreatywny naszego mózgu generuje listy możliwych odpowiedzi. Zadaniem modułu kreatywnego jest szybkie zaproponowanie możliwie dużej liczby odpowiedzi. Zupełnie jak w grze w kalambury, nie ma czasu na wartościowanie odpowiedzi, rzucamy możliwie szybko pomysły i skojarzenia, które nam przychodzą do głowy. Cechą szczególną modułu kreatywnego jest to, że nie może on odpowiedzieć “nie wiem, nie mam wystarczająco danych”. Jest tak, ponieważ krytyczna ocena, czy mamy wystarczająco dużo danych, wymaga więcej czasu i energii. Taka ocena może być przeprowadzona przez moduł krytyczny , o ile uznamy, że warto krytycznie oceniać odpowiedzi. Nawyk krytycznej oceny każdego lub prawie każdego osądu można sobie wyrobić, nie jest on jednak bynajmniej wrodzony. Bez względu jednak na to, czy moduł krytyczny działa, czy nie, kandydatów na odpowiedzi generuje moduł kreatywny.
Ale co, jeżeli nie mamy wystarczająco lub wręcz żadnych danych potrzebnych do udzielenia odpowiedzi na pytanie? Wtedy moduł kreatywny często automatycznie podmienia pytanie, na takie, na które potrafi udzielić odpowiedzi. W przypadku przyczyn śmierci, oryginalne pytanie: jaka przyczyna śmierci jest najczęstsza?, zostało zamienione na pytanie: o jakiej przyczynie śmierci często ostatnio słyszałeś? Podmiana pytania jest całkowicie automatyczna i dotyczy każdego pytania, z jakim się spotykamy. We wspomnianej książce podano przykład podmiany pytania: czy firma Ford jest w dobrej kondycji i czy warto zainwestować w jej akcje?, na pytanie: czy podobają mi się samochody Forda? Podmiana pytania tego typu często ma miejsce u “intuicyjnych” inwestorów.
Podmiana pytania często oznacza, że nie otrzymujemy właściwej odpowiedzi. Jak łatwo sobie wyobrazić, błędne oszacowanie prawdopodobieństwa jest przyczyną błędnych decyzji. Interesujący przykład konsekwencji takich pomyłek jest przedstawiony w książce [Steven Levitt and Stephen Dubner. Freakonomics: A Rogue Economist Explores the Hidden Side of Everything William Morrow, 2009] Opisano tam przypadek rodziców, którzy nie pozwalali córce bawić się w domu koleżanki, ponieważ znajdowała się tam broń i rodzice bali się, że może to jakoś doprowadzić do postrzelenia. Zamiast tego obie dziewczynki bawiły się w domu, przy którym znajdował się basen. Na pytanie, czy bardziej niebezpieczny dla małych dzieci jest basen przy miejscu zabaw, czy pistolet w szufladzie biurka, większość rodziców odpowie, że to drugie, gdyż bardziej obawia się broni. Częściej bowiem w filmach to broń czy mediach jest przyczyną zgonu niż basen.
Okazuje się jednak, że statystyki przyczyn zgonów dzieci wyraźnie pokazują, że kilkukrotnie większe ryzyko związane jest z obecnością basenu i możliwością utonięcia w basenie, niż z obecnością broni i możliwością postrzelenia dziecka. Dziewczynki z tego przykładu byłyby znacznie bezpieczniejsze, gdyby bawiły się w domu, gdzie jest broń. Jednak ocena ryzyka podświadomie przeprowadzona przez rodziców związana była nie z pytaniem: Czy moje dziecko będzie bezpieczniejsze w domu z basenem, czy w domu, w którym jest broń? ale z podmienionym pytaniem: Czy częściej słyszę o wypadkach spowodowanych bronią, czy spowodowanych utonięciem w basenie?
Takich przykładów można mnożyć. W książce [Steven Levitt and Stephen Dubner. SuperFreakonomics: Global Cooling, Patriotic Prostitutes, and Why Suicide Bombers Should Buy Life Insurance William Morrow, 2009] ci sami autorzy uzasadniali, dlaczego pijany pieszy ma większe szanse na udział w wypadku, niż pijany kierowca. Z tej perspektywy decyzja pijanej osoby, by wracać pieszo zamiast samochodem jest złą decyzją (oczywiście decyzja, by wracać samochodem, jest znacznie gorsza niż decyzja, by wracać taksówką lub innym środkiem komunikacji kierowanym przez trzeźwą osobę!!!). Jeszcze inne przykłady podobnych błędów oceny szansy i ryzyka można znaleźć w wystąpieniu Dlaczego podejmujemy złe decyzje [Dan Gilbert. Why we make bad decisions, 2005]
Pokazuje on wyniki badań, zgodnie z którymi ankietowani oceniali liczbę ofiar tornad w Stanach Zjednoczonych na wyższą od liczby ofiar astmy, w sytuacji, gdy w statystykach astma jest dwudziestokrotnie częściej przyczyną śmierci.
Nie jest jednak tak, że wyłączną winę za te błędne szacunki ponoszą media i ich skłonność do straszenia zdarzeniami rzadkimi. Przedstawię przykład podany w angielskiej wersji językowej przez Dana Gilberta, zaadaptowany przez mnie do języka polskiego. Odpowiedz, szanowny Czytelniku na następujące pytanie:
Rysunek 3: Najczęstsze przyczyny zgonów w roku 2010. Źródło: Podręczne dane statystyczne. SmarterPoland.pl, http://bit.ly/160RUaa
Czy w języku polskim jest więcej czteroliterowych słów rozpoczynających się od litery “r”, czy tych, które literę “r” mają na trzeciej pozycji?
r _ _ _ _ _ r _
Jeżeli ktokolwiek zna dokładnie częstości występowania słów z literą “r” to chyba jedynie skrabliści pasjonaci. Zdecydowana większość z nas nie zna odpowiedzi, musi więc ją oszacować. W jaki sposób najłatwiej oszacować te częstości? Trzeba przywołać z pamięci przykłady słów zaczynających się na literę “r” i przykłady słów mających literę “r” na trzeciej pozycji. Dochodzi do podmiany pytania na:
Czy potrafisz wymienić więcej czteroliterowych słów rozpoczynających się na literę “r”, czy czteroliterowych słów z literą “r” na trzeciej pozycji?
Oczywiście z uwagi na to, jak myślimy o słowach, znacznie łatwiej jest nam wymyślić słowo zaczynające się na literę “r”, niż słowo z literą “r” na trzeciej pozycji. Okazuje się jednak, że słów rozpoczynających się na literę “r” jest około 40% mniej niż tych, w których litera “r” występuje na trzecim miejscu.
W korpusie języka polskiego, z którego korzystałem, czteroliterowych wyrazów, rozpoczynających się od litery “r” jest 349, a czteroliterowych wyrazów z literą “r” występującą na trzeciej pozycji jest 564.
Największe błędy dotyczące oceny prawdopodobieństwa mają związek ze zdarzeniami bardzo rzadkimi, dla których nie mamy najczęściej żadnych intuicji. Powszechnym przykładem jest prawdopodobieństwo wygrania w loterii. Ponieważ widzimy i słyszymy w telewizji o osobach, które wygrywają miliony, oceniamy prawdopodobieństwo wygranej na bardzo małe, ale wciąż błędnie przeszacowujemy je o kilka rzędów wielkości.
Nie zawsze przeszacowujemy prawdopodobieństwa rzadkich zdarzeń, czasem je niedoszacowujemy. Nassim Taleb w swojej książce [Nassim Nicholas Taleb. The Black Swan: The Impact of the Highly Improbable Random House, 2007] przedstawia długą listę zdarzeń zdarzeń rzadkich a równocześnie przełomowych, zaskakujących, niosących duże zmiany, które wydawały się zdarzeniami zupełnie nieprawdopodobnymi, a się wydarzyły. Co więcej, zdarzenia nieprawdopodobne wydarzają się częściej, niż się nam wydaje. Taleb nazywa takie zdarzenia czarnymi łabędziami. W naszej percepcji nie ma miejsca dla zdarzeń rzadkich zachodzących raz na 30 lat. Po co się takimi zdarzeniami przejmować, gdy umysł ma nas bronić przed drapieżnikiem tu i teraz? Nie mamy żadnych intuicji dotyczących zdarzeń pojawiających się raz na 30 lat. Co więcej, gdy już takie nieprawdopodobne zdarzenie się wydarzy (bańka spekulacyjna na giełdzie, narodziny internetu, krach gospodarczy), to zostanie ono zracjonalizowane. Znaleźć można wielu ekspertów uważających, że taka firma jak Google musiała się pojawić, że taka sieć jak Internet musiała się pojawić, badających dlaczego musiała wybuchnąć druga wojna światowa, nawet uzasadniających, dlaczego krach gospodarczy sprzed kilku lat musiał zaistnieć.
Jest to oczywiście kolejny przykład błędu podmiany pytania. Gdy szacujemy prawdopodobieństwo zaistnienia takiego zjawiska jak druga wojna światowa i jednocześnie wiemy, że ta druga wojna światowa się wydarzyła, to jesteśmy podatni na przeszacowanie tego prawdopodobieństwa, ponieważ wiemy, że dane zdarzenie się wydarzyło.
Podmiana pytania to bardzo częste zjawisko, ponieważ odpowiedzi na większość pytań nie znamy, a nasz moduł kreatywny, czyli bezkrytyczna część mózgu, rozpaczliwie próbuje jakiejś odpowiedzi udzielić.
Problem podmiany pytania należy mieć na uwadze, projektując grafikę statystyczną. Jeżeli z wykresu nie będzie wystarczająco jasno wynikało, co on ma przedstawiać, odbiorca może go źle odczytać. Co więcej, może nawet nie wiedzieć, że go źle odczytuje! Aby uniknąć takich pomyłek, najlepiej przetestować zaprojektowaną grafikę na postronnym obserwatorze.
odra, afro, aura, bard, cera, cyrk, fort, góra, zero, wkra, rura, ...
Nie wszystko ma swoją przyczynę
Wiele problemów w odczytywaniu informacji pojawia się, gdy zbyt usilnie staramy się znaleźć zależności pomiędzy zdarzeniami. Czy jedzenie pomidorów pozwala na uniknięcie chorób? Czy zapisywanie dziecka na dodatkowe zajęcia przyczyni się do lepszych wyników w nauce? Czy w małych klasach można się więcej nauczyć? Czy lepiej karmić dzieci piersią? Wewnętrzna potrzeba spójności i potrzeba posiadania kontroli nad otoczeniem prowadzi do “odkrywania” przypadkowych relacji, które mają tendencje do obrastania w mity. Co więcej, gdy czytamy, że badacze falsyfikują jakąś hipotezę, przykładowo, że szpinak wcale nie zawiera nadzwyczajnie dużo żelaza, ale nie przykładamy do tego komunikatu dużej wagi, może się okazać, że zapomnimy o tym, że hipoteza była falsyfikowana, ale będziemy pamiętać, że o tej hipotezie czytaliśmy. Przez co, w drodze racjonalizacji, możemy zacząć traktować ją jako prawdziwą. W myśl zasady, że komunikaty, które wydają nam się znajome, uznajemy za prawdziwe.
Pokazaliśmy na przykładach, jak trudno jest zrozumieć duże liczby lub małe prawdopodobieństwa. Okazuje się, że jeszcze trudniej jest zrozumieć przypadkowość. Jesteśmy skłonni myśleć, że trudność w analizie danych polega na skojarzeniu oraz znalezieniu zależności pomiędzy dwoma cechami. Genialny analityk widzi morze liczb i nagle dostrzega w nich ukryty wzorzec niewidoczny dla innych.
A jeżeli problem leży zupełnie gdzie indziej? Jeżeli widzimy zbyt wiele fałszywych zależności, doszukując się znaczenia w zupełnie przypadkowych związkach? Co, jeżeli geniusz analityka polega na określeniu, które z zależności nie są przypadkowe? Z pewnością trudniej nakręcić film o analityku, który nie uznał jakiegoś związku za ważny i miał rację, albo o detektywie, który stwierdził, że większość zebranych wskazówek nie ma znaczenia. Ale jeżeli badamy problemy percepcji w komunikacji zależności, to jak pokażemy na przykładach, nasz mózg dopisuje znaczenia do zupełnie przypadkowych elementów posiadanego komunikatu i wiele wiedzy potrzeba, by odsiać te przypadkowe zależności.
Trudność zaakceptowania “zwykłego przypadku” pojawia się w bardzo wielu sytuacjach. Często jej nie dostrzegamy, ponieważ żyjemy w przekonaniu, że akurat to zjawisko nie jest przypadkowe, uznajemy więc wyjaśnienia jako uzasadnione. Ilustracje tego problemu zaczniemy od historii bombardowania Londynu. Poniższa grafika przedstawia miejsca zbombardowane przez niemiecką Luftwaffe w latach 1940/1941. Naloty te miały na celu zdemoralizowanie mieszkańców Londynu. Celem nie były strategiczne obiekty wojskowe, ale samo miasto. Oczywiście londyńczycy nie wiedzieli, a przynajmniej nie wszyscy wiedzieli, jaki jest cel przeprowadzania nalotów dywanowych i bombardowania przypadkowych budynków cywilnych.
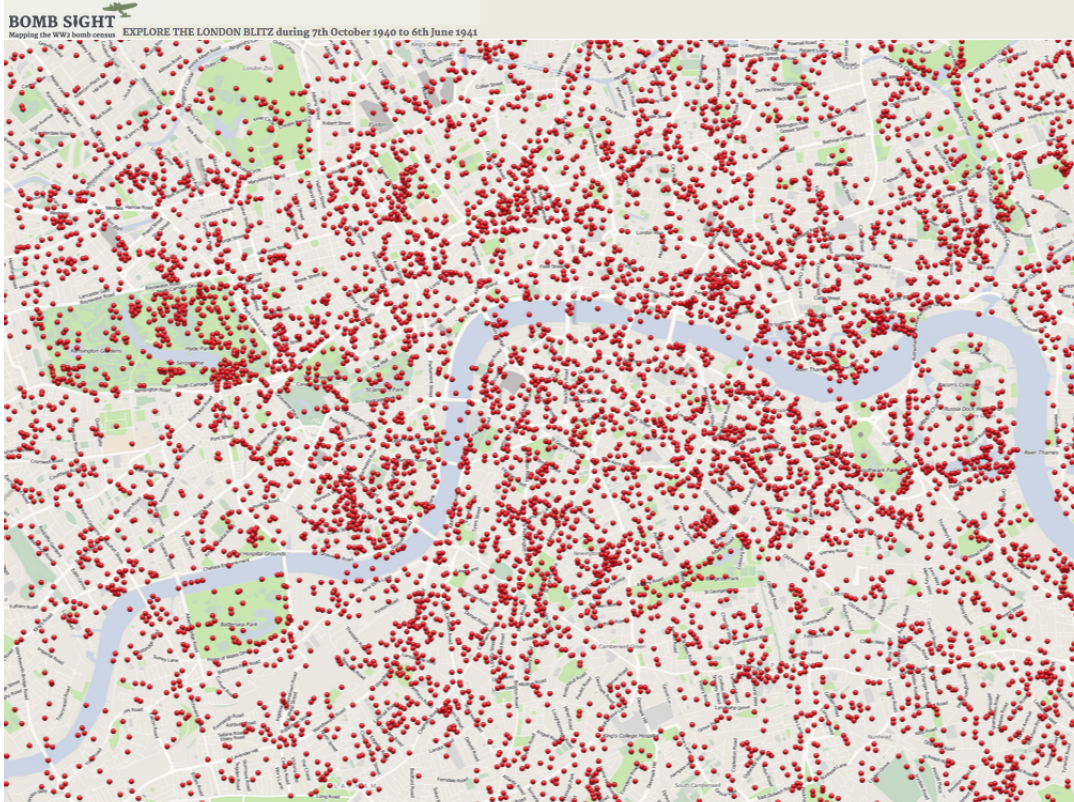 Rysunek 4: Mapa miejsc, na które zrzucono bomby podczas nalotów Londynu. Źródło: http://bombsight.org/
Rysunek 4: Mapa miejsc, na które zrzucono bomby podczas nalotów Londynu. Źródło: http://bombsight.org/
Mieszkając w Londynie i widząc, gdzie spadały bomby częściej, a gdzie rzadziej, Londyńczycy doszukiwali się wzorców, szukając celów niemieckich ataków. W budynkach/ulicach/ osiedlach, na które nie spadły bomby doszukiwano się szpiegów lub kolaborantów, którzy są przez agresora oszczędzani. W miejscach, gdzie spadło szczególnie wiele bomb, doszukiwano się wyjątkowo istotnych strategicznie celów. Jest to racjonalne i bardzo ludzkie zachowanie, by widząc, że na jakiś budynek bomba spadła dwa razy, podczas gdy na sąsiednią ulicę nie spadła żadna bomba doszukiwać się przyczyn, racjonalizować sobie świat, aby wyciągnąć wnioski na przyszłość i uratować swoje życie.
Dziś jednak, mając zebrane informacje o miejscach, gdzie zrzucono bomby, można przeprowadzić analizę statystyczną, by określić, czy częstość, z jaką bomby spadały w różne miejsca, jest istotnie różna od częstości, która pojawiłaby się, gdyby bomby spadały w losowe miejsca.
Intuicja większości osób nie jest wystarczająco wyćwiczona, by ocenić, czy wylosowanie 4 orłów w 6 rzutach monetą jest bardzo nieprawdopodobne (czyli prawdopodobieństwo jest bardzo bardzo małe) dla zwykłej symetrycznej monety. Ale już mając możliwość spokojnego policzenia tego prawdopodobieństwa, większość osób poradziłaby sobie z rachunkami.
Podobnie sprawa ma się w badaniu, na ile skupiska bombardowanych miejsc są większe niż wynikałoby z losowości. Okazuje się, że analiza statystyczna miejsc bombardowania z użyciem testów losowości $\chi^2$ lub z użyciem dwuwymiarowych pól losowych pokazuje, że rozkład miejsc, na które zrzucono bomby, jest zgodny z rozkładem zupełnie przypadkowym. Większe zagęszczenie bomb w pewnych miejscach i mniejsze zagęszczenie w innych miejscach jest typowe dla zdarzeń losowych. Jeżeli całą mapę podzielimy na regularną kratę i zliczymy, ile jest kwadratów, na które nie spadła żadna bomba, ile jest takich, na które spadła jedna bomba, dwie bomby itp, okaże się, że liczba tych kwadratów jest zgodna z oczekiwaną przy zupełnie losowym bombardowaniu. Patrząc na mapę, nie sposób jednak oprzeć się wrażeniu, że widzimy “wyraźne” wzorce.
Skąd się bierze to doszukiwanie zależności przyczynowo-skutkowych? W pewnym sensie sami ćwiczymy mózg w nieustannym generowaniu sugestywnych zależności. Gdy przed szkołą podstawową pięciolatki są oceniane pod kątem zdatności do rozpoczęcia nauki w szkole podstawowej, sprawdza się między innymi, czy dziecko potrafi ułożyć przyczynowo-skutkową historię z kilku obrazków. Oczekuje się od dziecka, że będzie dostrzegało przyczynowo-skutkowe zależności wcześniej niż nauczy się liczyć do dziesięciu, sylabizować czy czytać.
Skoro umiejętność szukania skojarzeń jest tak wysoko ceniona, nic więc dziwnego, że ćwiczymy się w umiejętności dostrzegania zależności, mniejszą wagę przykładając do ryzyka, że dostrzeżemy nieistniejącą zależność. Problem ulegania złudzeniu istotnych zależności tam, gdzie tych zależności nie ma, dotyka nie tylko przeciętnego Kowalskiego, ale również naukowców stosujących statystykę na co dzień. Jest to jeden (z pewnością nie jedyny) z powodów, dla których zasypywani jesteśmy śmieciowymi pseudo odkryciami o cudownych właściwościach różnych diet, substancji, strategii.
Bardzo ciekawy eksperyment, pokazujący pierwotną potrzebę doszukiwania się przyczynowo-skutkowych zależności, pokazał w 1946 roku Albert Michotte. W przeprowadzonym eksperymencie pokazywał animację, w której na początku widać było przemieszczający się niebieski dysk w stronę czerwonego dysku, a następnie przemieszczający się czerwony dysk. Obserwatorzy, zapytani co widzą, opisywali niebieską kulkę, która uderza w czerwoną kulkę. Czerwona kulka przemieszcza się ponieważ została uderzona. W rzeczywistości była to jednak sekwencja obrazków dwóch kół, nie ma więc mowy o fizycznej przyczynowo-skutkowości. Obserwatorzy opisywali tę zależność jak przyczynowo-skutkową, choć doskonale widzieli, że to jedynie koła na kartce. Efekt ruchu czerwonej kulki jako następstwo uderzenia przez niebieską jest całkowicie domniemany.
Okazuje się, że obserwatorzy skłonni są do przypisywania nie tylko zależności przyczynowo-skutkowych, ale też dodają intencje i przypisują zamiary tam, gdzie ich być nie może. W połowie lat 40. Fritz Heider przeprowadził eksperyment z animacją trójkątów i okręgu zmieniającego pozycje. Podczas animacji dwa trójkąty i okrąg wyświetlane były w ten sposób, by zasugerować, że dochodzi do przemieszczania się tych obiektów.
 Rysunek 5: Zobacz animację eksperymentu pod tym adresem http://bit.ly/1bJ4h3w
Rysunek 5: Zobacz animację eksperymentu pod tym adresem http://bit.ly/1bJ4h3w
Heider pytał obserwatorów o to, co widzieli. Animacja okazała się na tyle sugestywna, że większość pytanych opowiadała historie, w których duży zły trójkąt niewoli mały okrąg, a ten zostaje uwolniony przez mały trójkąt. Niektórzy szli dalej, kojarząc okrąg i trójkąt ze zniewoloną księżniczką uratowaną przez odważnego rycerza. Cała historia domniemana z sekwencji różnych pozycji trzech figur geometrycznych.
Przykładów takich zaskakujących zależności w otaczającym świecie znajdziemy dużo więcej. Wszystkie one pokazują, jak desperacko nasz umysł szuka zależności przyczynowo-skutkowych, które upewniają go w spójnej, kontrolowanej i zrozumiałej wizji świata. Przypadkowość i brak związku to pojęcia dla naszego mózgu niepożądane.
W ostatnich latach można znaleźć coraz więcej książek i artykułów zbierających najciekawsze przykłady nieistniejących zależności odkrywanych i potwierdzanych przez kolejnych badaczy, albo przykłady racjonalizacji zdarzeń, które jednak mają wszelkie znamiona zdarzeń zupełnie przypadkowych. W książce [Duncan Watts. Everything Is Obvious: *Once You Know the Answer Crown Business, 2011] autor pokazuje na przykładach jak łatwo zracjonalizować prawdę ogólną, która jest wspierana tylko przez “społeczny dowód”: jest prawdą, bo wszyscy w nią wierzą.
 Rysunek 6: Zobacz animację eksperymentu pod tym adresem http://bit.ly/1cyI1sB
Rysunek 6: Zobacz animację eksperymentu pod tym adresem http://bit.ly/1cyI1sB
Jeden z ciekawszych przykładów z tej książki dotyczy analizy popularności obrazu Leonarda da Vinci Mona Lisa Autor przyznaje, że nie jest krytykiem sztuki, ale zderza popularne opinie uzasadniające, dlaczego akurat ten obraz jest uznawany za najcenniejszy obraz na świecie. Oczywiście Mona Lisa nie jest na sprzedaż, więc określenie “najcenniejszy” dotyczy kwoty, na którą ten obraz jest ubezpieczony. Okazuje się, że dyskusja cech genialnych tego obrazu sprowadza się do określenia, że jest on tak wartościowy, ponieważ ma cechy X, Y i Z, ale mówimy, że te cechy się liczą, ponieważ ma je właśnie ten obraz. Innymi słowy mówimy, że Mona Lisa jest najcenniejszym obrazem, ponieważ jest podobna do Mony Lisy, która jest najcenniejszym obrazem.
Można sobie jednak wyobrazić, że historia potoczyła się inaczej i to inny obraz został uznany za najcenniejszy. Być może to, który z obrazów jest najcenniejszy jest cechą całkowicie przypadkową, niezwiązaną z konkretnymi cechami samego obrazu, a nawet jeżeli związaną, to w sposób, którego nie da się uzasadnić. Dla wielu osób taki styl myślenia jest jednak nie do przyjęcia, jak to bowiem możliwe, że Mona Lisa nie ma cech obrazu wybitnego, skoro jest wybitnym obrazem? Jeszcze bardziej nie do pomyślenia jest stwierdzenie, że być może nie ma czegoś takiego jak cechy obrazu wybitnego.
Spójrzmy na tego typu błąd percepcji z naszego rodzimego podwórka. Jednym z najciekawszych błędów ilustrujących potrzebę przyczynowo-skutkowych relacji jest interpretacja wyników z sondaży poparcia politycznego. Główne ośrodki badania opinii publicznej przeprowadzają sondaże poparcia partii politycznych co miesiąc lub częściej. Zazwyczaj wielkość próby oscyluje w okolicach 1000 osób, z czego około połowa nie wie, kogo poprze, lub nie popiera nikogo. Pozostaje więc około 500 osób na bazie których szacowane jest poparcie. Wyniki tego poparcia są prezentowane w mediach zazwyczaj bez żadnej refleksji dotyczącej błędu pomiaru. Są za to porównywane z wynikami poprzedniego sondażu, co dodatkowo zwiększa błąd oszacowania, jeżeli chodzi o ocenę zmiany poparcia.
 Rysunek 7: Mona Lisa autorstwa Leonarda da Vinci.
Rysunek 7: Mona Lisa autorstwa Leonarda da Vinci.
Przyjrzyjmy się sondażowi Homo Homini z 20 listopada 2012 roku. Na bazie tego sondażu podano, że poparcie dla Platformy Obywatelskiej wynosi 36% i jest to wzrost o 5 punktów procentowych w stosunku do poprzedniego sondażu. Te pięć punktów to dużo, więc w mediach eksperci wypowiadali się, co mogło spowodować tak duży wzrost.
sondaz.wp.pl
W kolejnym sondażu z 5 grudnia 2012 roku poparcie spadło do poziomu 29%. Mamy więc spadek o 7 punktów procentowych. W mediach eksperci wskazują, co rząd robił źle, że zaowocowało to takim spadkiem poparcia.
sondaz.wp.pl
Dwa tygodnie później, 19 grudnia, poparcie w sondażu wynosiło 33%, a więc wzrost o 4 punkty. I eksperci wyjaśniają, skąd ten duży wzrost poparcia, mówią, że to koniec roku tak wpływa podsumowania wyborców.
sondaz.wp.pl
Mają na wyjaśnienie mało czasu, bo już 8 stycznia 2013, w kolejnym sondażu poparcie Platformy wynosi znów 29%, a więc spadek o 4 punkty. Czy to przypadek, że w kolejnych sondażach na zmianę poparcie bardzo rosło i bardzo spadało? Przy wahaniu poparcia: 31%, 36%, 29%, 33%, 29%, bardziej prawdopodobne jest stwierdzenie, że zmiany te związane są z błędem pomiaru, a nie znacznymi wahaniami poparcia obserwowanymi co dwa tygodnie.
Zamiast analizować wyniki pięciu kolejnych sondaży, przyjrzyjmy się wynikom z 53 sondaży przeprowadzonych przez Homo Homini w okresie ostatnich 2 lat. Zestawmy, jak wyglądały zmiany poparcia dla Platformy Obywatelskiej w każdej parze kolejnych dwóch sondaży. Ponieważ wszystkich zebranych sondaży mamy 53, więc możemy dla 52 par kolejnych sondaży policzyć, jak wyglądała zmiana pomiędzy kolejnymi dwoma sondażami. A dla 51 par takich par możemy porównać dwie kolejne zmiany.
sondaz.wp.pl

Powyższa tabela pokazuje, że najczęściej (oczywiście nie zawsze) po wzroście poparcia przychodzi spadek. Z pewnością eksperci znajdą jakieś wytłumaczenie zmian poparcia, ale czy nie jest bardziej prawdopodobne, że wzrosty i spadki poparcia są głównie skutkiem niewielkiej wielkości próby i czystej przypadkowości?
Nie twierdzę tutaj, że poparcie dla partii się nie zmienia. Z pewnością się zmienia, ale te zmiany są powolne i możliwe do wychwycenia w dłuższym horyzoncie czasu lub przy większej próbie. Dla małych prób znaczny procent wzrostów i spadków poparcia wynika z dokładności pomiaru. Problem ten oczywiście nie dotyczy komentarzy wyników z sondaży Homo Homini, ale w mniejszym czy większym stopniu każdej innej agencji sondażowej.
Oczywiście przyznanie się do tego słabo wyglądałoby w gazetach i telewizji. Co miałby powiedzieć ekspert zapytany, dlaczego poparcie wzrosło o 5 punktów procentowych? Stwierdzenie, że to może być zwykły przypadek, może i jest prawdziwe, ale nasz umysł pożąda przyczyn, racjonalizuje losowe fluktuacje. Paradoksalnie taka racjonalizacja daje poczucie zrozumienia, skąd te zmiany się biorą. Paradoksalnie, bowiem tak naprawdę jest dowodem niezrozumienia losowości i niepewności pomiaru stojącej za sondażami opinii publicznej.
Rysunek 8: Tabela przedstawiająca jak często po wzroście/spadku poparcia dla PO badanego przez ośrodek Homo Homini następuje wzrost/spadek poparcia w kolejnym badaniu. Źródło: opracowanie własne
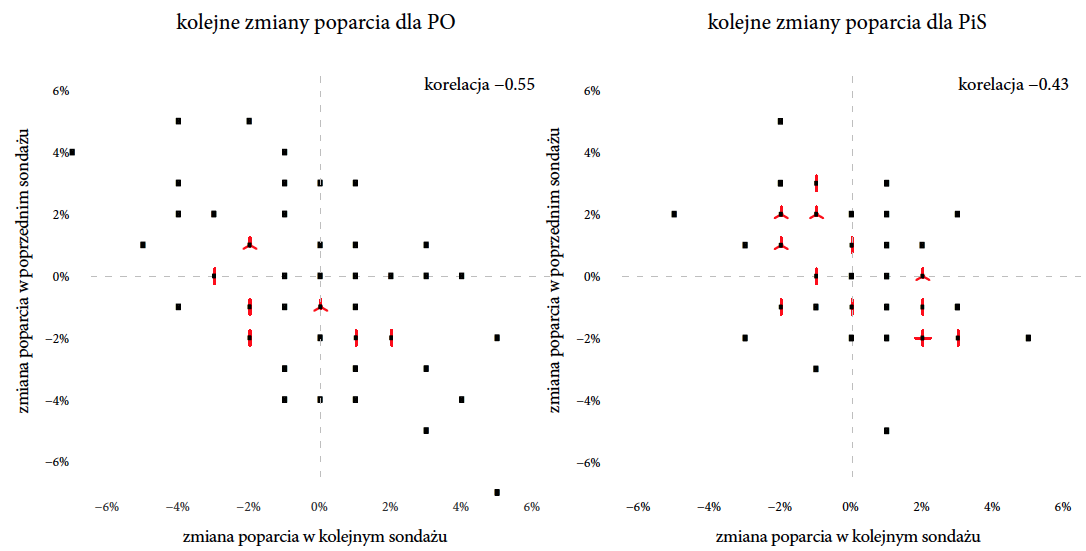 Rysunek 9: Ilustracja zjawiska “powrotu do średniej”. Prezentowane są sondaże wykonane przez Homo Homini w okresie 2011–2013. Jeżeli punkty nachodzą na siebie, liczbę nakładających się punktów zaznaczono czerwonymi listkami. Z reguły, prezentując wyniki sondażu, pokazuje się również o ile poparcie wzrosło/spadło w stosunku do poprzedniego sondażu. Dla wielu komentatorów jest to świetna okazja, by szukać uzasadnień dla dużych zmian poparcia. Dlaczego poparcie spadło o 5%? Z pewnością coś się stało. Jednak poparcie badane na niewielkiej próbie około 1000 osób ma naturalną tendencję do fluktuacji wokół pewnej wartości. Nagłe wzrosty lub spadki w dużej części są przypadkowe, dlatego w kolejnym sondażu sytuacja najczęściej wraca do średniej. Źródło: opracowanie własne
Rysunek 9: Ilustracja zjawiska “powrotu do średniej”. Prezentowane są sondaże wykonane przez Homo Homini w okresie 2011–2013. Jeżeli punkty nachodzą na siebie, liczbę nakładających się punktów zaznaczono czerwonymi listkami. Z reguły, prezentując wyniki sondażu, pokazuje się również o ile poparcie wzrosło/spadło w stosunku do poprzedniego sondażu. Dla wielu komentatorów jest to świetna okazja, by szukać uzasadnień dla dużych zmian poparcia. Dlaczego poparcie spadło o 5%? Z pewnością coś się stało. Jednak poparcie badane na niewielkiej próbie około 1000 osób ma naturalną tendencję do fluktuacji wokół pewnej wartości. Nagłe wzrosty lub spadki w dużej części są przypadkowe, dlatego w kolejnym sondażu sytuacja najczęściej wraca do średniej. Źródło: opracowanie własne
Ta losowość dotyczy oczywiście każdej partii i każdego ośrodka badającego sondażowo opinie, ale wpływ losowości najłatwiej zauważyć dla partii, które mają duże poparcie. Na rysunku 9 prezentowane są graficznie zmiany poparcia w sondażach dla Platformy Obywatelskiej i Prawa i Sprawiedliwości w okresie 2011–2013.
Podobną “ujemną korelację” zaobserwować można w skokach narciarskich. Gdy jeden narciarz skoczy wyjątkowo dobrze, znacznie powyżej oczekiwań, to najczęściej drugi skok będzie gorszy niż pierwszy, co często komentatorzy nazywają “zepsuciem” skoku. Podobnie, gdy pierwszy skok będzie poniżej oczekiwań, to drugi skok będzie lepszy niż pierwszy, a skoczek się “poprawił”. Zjawisko to jest czasem nazywane “powrotem do średniej/przeciętnej”, ponieważ dla wielu mechanizmów losowych najczęściej obserwuje się wartości bliskie średniej typowej dla tego mechanizmu. Nawet jeżeli przypadkowo zaobserwujemy nadzwyczaj wysoką lub niską wartość, nie ma najczęściej powodu, by kolejna obserwacja była również tak wyjątkowa. Zazwyczaj po wyjątkowo dziwnej wartości kolejna jest znów bliska średniej.
Termin “powrotu do średniej” został spopularyzowany przez Francisa Galtona (1822-1911) [Francis Galton. Regression towards mediocrity in hereditary stature. The Journal of the Anthropological Institute of Great Britain and Ireland, page 246–263, 1886], który użył go opisując wyniki badań pokazujących, że synowie bardzo wysokich ojców są niżsi niż ojcowie, ich wzrost jest bliższy średniej. Ten powrót do średniej Galton określił słowem regression, terminem, który później zaczął być używany do nazywania metod badania zależności pomiędzy zmiennymi.
W książce [Daniel Kahneman. Thinking, Fast and Slow Farrar, Straus and Giroux, 2011] przedstawiono jeszcze inny przykład, gdy zjawisko “powrotu do średniej” jest racjonalizowane i dopisywana jest do niego przyczynowo-skutkowa historia. Jako przykład podano wpływ napoi energetycznych na stan dzieci w głębokiej depresji. Przedstawiono hipotetyczne badanie, w którym dzieciom o obniżonym nastroju podaje się napój energetyczny i następnie obserwuje się efekt poprawy. Okazuje się, że dzieciom nastrój się poprawia. Czyż to nie jest fantastyczne odkrycie? Nie, ponieważ gdyby dzieciom w obniżonym nastroju nic nie podawać to średnio ich nastrój również by się poprawił, ponieważ nastrój, jak i wiele innych cech, krąży wokół pewnej średniej i czasem jest obniżony, a czasem podwyższony
Dlaczego obsesyjnie szukamy wyjaśnień? Czy dają nam poczucie kontroli? W książce [Nassim Nicholas Taleb. The Black Swan: The Impact of the Highly Improbable Random House, 2007] podano ciekawy przykład zachowania się rynku w dniu, w którym pojmano Saddama Husseina. Najpierw rynek zanotował wzrosty, a po pół godzinie spadki. W obu przypadkach jako przyczynę podawano schwytanie Husseina. Najważniejsza wiadomość dnia musiała (zdaniem ekspertów) mieć wpływ na zachowanie się rynku. Ale że jednocześnie była przyczyną wzrostów i spadków?
Zaskakująca przypadkowość
W obiegu powszechnym funkcjonuje sformułowanie “prawo serii” opisujące sytuacje, gdy jakieś rzadkie zjawisko występuje nagle kilka razy pod rząd. Zauważamy takie sytuacje, ponieważ są wbrew naszym wyobrażeniom dotyczącym zjawisk rzadkich, skoro coś jest rzadkie, to zdarza się rzadko, a już z pewnością nie zdarza się dwa razy pod rząd.
Tymczasem często nawet losowe zjawiska generują losowe serie częściej niż byśmy się tego spodziewali. Mój wykładowca rachunku prawdopodobieństwa, prof. Tomasz Żak, przedstawiał przykład testu na uczciwość studenta. Test wygląda następująco: prowadzący zadaje pracę domową polegającą na wykonaniu 1000 rzutów monetą oraz zapisanie wyników w zeszycie. Student ma do wyboru: A) nie wykonać pracy domowej (na naszym wydziale ta opcja nie wchodziła w grę, więc jej nawet nie rozważaliśmy), B) rzucić 1000 razy monetą i spisywać kolejne wyniki, co jest dosyć żmudnym zajęciem, C) zmyślić wyniki rzutów i wpisać do zeszytu przypadkowe wartości.
Okazuje się jednak, że prowadzący ma dosyć dobry test losowości. Gdy myślimy o tym, jak często w takim ciągu orłów i reszek występują serie kolejnych identycznych wyników o długości 8 lub większej, zazwyczaj intuicja nas zawodzi. Zwykły student, nieznający jeszcze meandrów rachunku prawdopodobieństwa, prawdopodobnie wygeneruje ciągi reszek i orłów różnych długości, ale będzie unikał ciągów o długości 8 lub większej. A tym czasem średnio w 1000 elementowym ciągu losowych reszek i orłów wystąpią cztery serie przynajmniej 8 jednakowych wyników pod rząd. Kto by się spodziewał, że takie długie serie nie są czymś aż tak nadzwyczajnym?
Mit jedynej prawdziwej historii
Problemów związanych z percepcją danych jest wiele, ale najtrudniejszy jest problem z wiarą w jedną jedyną prawdziwą historię. Z jednej strony zdajemy sobie sprawę, że żyjemy w złożonym świecie, w którym różne czynniki wchodzą w interakcje, a skutki tych interakcji bywają nieprzewidywalne. Z drugiej strony ta złożoność nam przeszkadza i gdzieś tam głęboko wierzymy, że uda się złożone zależności sprowadzić do prostego wytłumaczenia. Czasem udaje się to zrobić, ale często popełniamy błąd zbyt wielkich uproszczeń.
Jest to spory problem, gdy opowiadamy jakąś historię. Gdy jej celem jest perswazja, usunięcie wszelkich wątpliwości jest dobre dla wiarygodności historii. Tak często postępują dziennikarze lub pisarze, którzy prezentując historię, chcą nam ją pokazać z określonej perspektywy tak, by cała historia prowadziła do określonych konkluzji. Jeżeli w historii są niespójności, to się je ukrywa, mocniej lub słabiej akcentując odpowiednie elementy. Ale jeżeli chcemy zrozumieć pewne zjawisko, albo pomóc w jego zrozumieniu odbiorcy, to często dobrze jest też przedstawić alternatywy.
Jeden z najciekawszych przykładów ilustrujących niebezpieczeństwa jednej historii przedstawiono w książce [Ian Ayres. Super Crunchers: Why Thinking-By-Numbers is the New Way To Be Smart Bantam, 2008]. Problem dotyczył lekarzy, którzy diagnozując, starali się znaleźć chorobę najlepiej pasującą do objawów. Gdy objawy są niestandardowe, taka diagnoza jest bardzo złożoną łamigłówką. Okazuje się jednak, że wybór najbardziej prawdopodobnej choroby wcale nie jest najlepszą strategią dla diagnosty. Co bowiem, jeżeli druga mniej prawdopodobna opcja wymaga zdecydowanie bardziej radykalnych środków?
Okazuje się, że w chwili, gdy lekarz rozwiązuje te trudne puzzle i znajduje prawdopodobną przyczynę choroby, popada w przesadne zaufanie do swojej diagnozy. I nawet jeżeli wybrał najbardziej prawdopodobną opcję, to jednak zawsze jest szansa, że ta opcja nie jest właściwa. A gdy w grę wchodzi zdrowie lub życie pacjenta, warto, by lekarz rozważył też inne opcje, może mniej prawdopodobne, ale wciąż możliwe i wykonał dodatkowe badania, by wykluczyć inne alternatywy.
Rozważmy zmyślony przykład. Zestaw objawów, dla którego można określić, że na 90% odpowiada za niego grypa, a na 10% gruźlica. Co zrobiliby diagności z serialu Doktor House w takim przypadku? Zebrani wokół stołu, obrzucani docinkami przez szefa, podaliby te prawdopodobieństwa, uznali że dziewięć razy bardziej prawdopodobna jest grypa i rzucili się do aplikowania choremu jakiejś terapii. Jednak grypa to względnie niegroźna choroba (choć grożąca ciężkimi powikłaniami). Nawet jeżeli jest bardziej prawdopodobna, to taka diagnoza bez wykonania dodatkowych testów oznaczałaby, że z takimi objawami u jednego pacjenta na dziesięć błędnie by zdiagnozowano grypę zamiast gruźlicy. Podczas gdy gruźlica jest znacznie poważniejszą chorobą, która nieleczona może prowadzić do śmierci.
Widzimy, że warto, by lekarz zadał sobie pytanie, “jeżeli nie grypa to co?”. Takie pytanie może doprowadzić do dodatkowych badań, które potwierdzą lub wykluczą gruźlicę. W serialach prawdziwą chorobę zdiagnozuje genialny House na podstawie zapachu potu pacjenta, ale co się stanie w realnym świecie?
W medycynie ten problem jest rozwiązywany za pomocą specyficznych systemów rekomendacyjnych. Jednym z nich jest system Isabel, który po wpisaniu symptomów generuje listę nawet kilkudziesięciu możliwych przyczyn. System ten nie wskazuje jedynie najbardziej prawdopodobnej przyczyny, nawet nie sortuje przyczyn względem ich prawdopodobieństwa (wtedy pojawiałaby się pokusa brania pod uwagę tylko tych prawdopodobnych), ale pełni rolę szerokiej listy typu “czy rozważyłeś taką możliwość ...” lub “czy wykonałeś badanie...”. Mając taką szeroką listę, łatwiej jest lekarzowi określić, jakie potencjalne hipotezy co do choroby należy zweryfikować. Pozwala też uwolnić się od zamknięcia na mniej prawdopodobne, ale wciąż możliwe przyczyny.
Nie tylko w zawodzie lekarza ważne jest kwestionowanie własnych obserwacji i poszukiwanie alternatywnych wytłumaczeń. W zawodzie analityka taka dociekliwość jest wręcz nieoceniona. Przyjrzyjmy się ciekawemu przykładowi z naszego lokalnego podwórka, a dokładniej z raportu [Krystyna Szafraniec. Mlodzi 2011. Kancelaria Prezesa Rady Ministrow, 2011] Chodzi mianowicie o porównanie odpowiedzi 19-letniej młodzieży na pytanie Co jest w życiu ważne? Badania takie przeprowadzono w latach 1976 i 2008. Celem było określenie, jakie wartości są wspólne dla tych dwóch pokoleń, a jakie są różne.
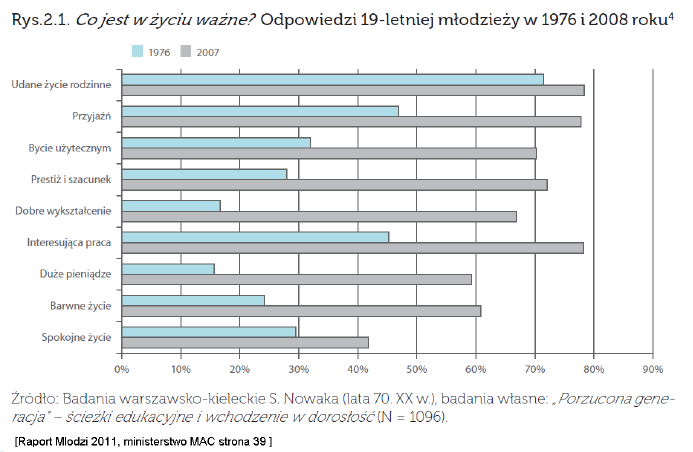
Wyniki z obu badań przedstawiono za pomocą wykresu słupkowego (rysunek 10). Jaki wniosek wysnuto na podstawie zestawienia tych badań? Przytoczę poniżej akapit ze strony 40 wspomnianego raportu.
Najprostsze porównywalne dane ukazują niezmiennie wysoką w hierarchii ważności pozycję rodziny – udane życie rodzinne jest podkreślane jako sprawa bardzo ważna zarówno przez dawne, jak i przez nowe młode pokolenie (przez nowe nawet bardziej). W tym słowie “kluczu” zawiera się szczęście osobiste i miłość, najwyżej dziś cenione przez najmłodsze kohorty młodzieży. Drugie podobieństwo dotyczy relatywnie niskiego wartościowania spokojnego życia. W innych kwestiach charakterystyki dawnej i nowej młodzieży wyraźnie się rozchodzą. Dzisiejsza młodzież dalece bardziej ceni sobie nie tylko dobre wykształcenie, interesującą pracę, duże pieniądze czy barwne życie – a więc wartości najczęściej jej przypisywane, lecz również przyjaźń, poczucie bycia potrzebnym i użytecznym, prestiż i szacunek u ludzi (cechy najbardziej kojarzone ze współczesną młodzieżą).
Oceniono więc, że takie wartości jak “udane życie rodzinne” i “spokojne życie” są podobnie oceniane przez oba pokolenia, podczas gdy pozostałe wartości oceniane są różnie. Taki wniosek uzasadniony jest porównaniem długości słupków, w przypadku “udanego życia rodzinnego” i “spokojnego życia” słupki obu kolorów mają podobną długość.
Czy to jednak jedyna możliwa interpretacja tych wyników? Czy jest w nich druga historia i czy ta druga historia nie jest nawet bardziej prawdopodobna niż pierwsza?
Rysunek 10: Wykres przedstawia wyniki dwóch różnych badań, na bazie których oceniono częstość odpowiedzi na pytanie Co jest w życiu ważne przez 19-letnią młodzież. Jedno badanie było realizowane w roku 1976, a drugie 32 lata później w 2008 roku. Źródło: rysunek 2.1 z raportu Młodzi 2011
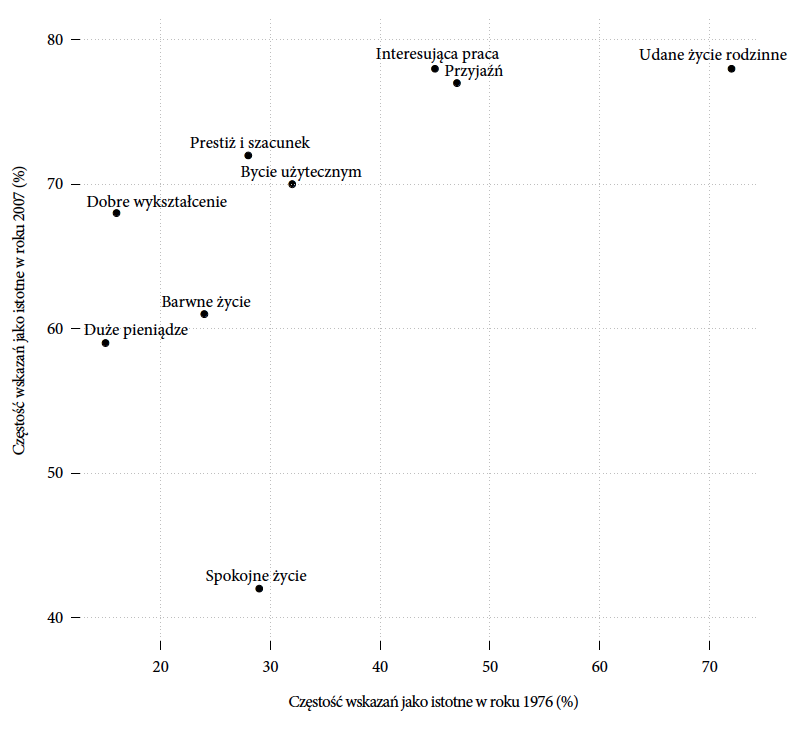
Dla mnie sygnałem, że być może w tej historii jest drugie dno, była obserwacja, że wszystkie słupki dla badania z roku 2008 są dłuższe niż te dla badania z 1976. Być może ankietowani mogli zaznaczyć więcej odpowiedzi, być może próg ważności był inaczej dobrany w tych dwóch badaniach, a być może młodzież w roku 2008 uważa, że więcej rzeczy jest ważnych w życiu. Bez względu na to, która z tych przyczyn jest prawdziwa, wydało mi się zasadne porównanie nie tylko proporcji osób oceniających daną wartość za ważną, ale porównanie hierarchii ważności dla obu pokoleń.
Co ciekawe, po zestawieniu rankingów wartości okazuje się, że wyłania się z nich zupełnie inna historia. Rankingi w obu pokoleniach są podobne. Trzy najważniejsze wartości to: “udane życie rodzinne”, “przyjaźń” i “interesująca praca”. Następne w rankingu są “bycie użytecznym” i “prestiż i szacunek”. Na końcu rankingu dla obu pokoleń są “barwne życie”, “dobre wykształcenie” i “duże pieniądze”. Największa zmiana pomiędzy tymi pokoleniami dotyczyła wartości “spokojne życie”, która kiedyś znajdowała się w środku stawki, a dla współczesnych 19-latków spadała na ostatnie miejsce.
Te same dane przedstawione na dwa różne sposoby ukazują dwie różne historie. W przypadku wartości “spokojne życie” te historie są skrajnie różne. Przywiązanie do jednej nie pozwala na dostrzeżenie drugiej, a jedynie widząc obie, możemy pełniej spojrzeć na podobieństwa i różnice pomiędzy pokoleniami. Osobiście bardziej przemawia do mnie historia z hierarchią ważności. Więcej na ten temat można przeczytać w artykule Młodzi 2011 na stronie http://bit.ly/1a7MDCG.
Inne interesujące oblicze problemu jednej historii związane jest ze stereotypowym myśleniem. Przedstawimy je na bazie zmodyfikowanego przykładu z książki Pułapki myślenia (czyli polskiego tłumaczenia książki [Daniel Kahneman. Pul{apki my'slenia. O my'sleniu szybkim i wolnym}. Media Rodzina, 2012]). Przykład ten w oryginale ilustruje trudność z szacowaniem prawdopodobieństwa zdarzeń, ale jest również dobrą ilustracją problemu jednej historii.
Wyobraźmy sobie energiczną i pracowitą 40-letnią kobietę o imieniu Dorota. Ma ona dwuletnią córeczkę o imieniu Emilka, która właśnie uczy się mówić i właśnie z dumą opanowała zdanie “mama da”. Emilka jest śliczną małą dziewczynką, bardzo radosną i bardzo dużą, oczywiście jak na swój wiek. Uwielbia zwiedzać każdy zakamarek mieszkania i jest ciekawa świata. Emilka, podobnie jak i Dorota, ma długie czarne włosy związane w kucyk.
Mając ten opis na uwadze, oceńmy, która z poniższych możliwości jest bardziej, a która mniej prawdopodobna?
[A] Dorota oddaje Emilkę do sierocińca.
[B] Dorota jest samotna, ma piątkę starszych dzieci, nie jest w stanie ich wszystkich utrzymać i oddaje córeczkę do sierocińca.
W jaki sposób, mając takie szczątkowe informacje, będziemy szacować, czy bardziej prawdopodobna jest odpowiedź A czy B? Oba zdarzenia są mało prawdopodobne, co więcej stoją w sprzeczności z naszym wyobrażeniem Doroty i Emilki, które sobie zbudowaliśmy po przeczytaniu powyższego opisu.
W większości przypadków takie szacowanie odbywa się na zasadzie określania, która z odpowiedzi najbardziej pasuje nam do przedstawionego wizerunku Doroty. A ponieważ opis przedstawiał Dorotę jako sympatyczną osobę oceniając prawdopodobieństwo poszukamy raczej odpowiedzi spójnej, uzasadniającej decyzję o oddaniu Emilki do sierocińca. Z tej perspektywy to opis B wydaje się bardziej wiarygodny. W samej rzeczy, w podobnych badaniach dotyczących hipotetycznej Lindy i jej hipotetycznego miejsca pracy, David Kahneman z zaskoczeniem odkrył, że pytani częściej odpowiadali, że to odpowiedź B jest bardziej prawdopodobna niż odpowiedź A, ponieważ właśnie dodatkowe szczegóły uwiarygadniały mało prawdopodobny scenariusz.
Rzecz w tym, że tak w powyższym przykładzie, jak i w badaniach Kahnemana, aby spełniać warunek B trzeba też spełniać warunek A, więc odpowiedź A jest bardziej prawdopodobna niż odpowiedź B, ponieważ jest ogólniejsza.
Problem z poprawnym wyborem najbardziej prawdopodobnej odpowiedzi jest związany z wstępnym wyobrażeniem sobie Doroty. Choć opis tej osoby był szczątkowy, to został on uspójniony o stereotypowe wyobrażenie kobiety pasującej do opisanych cech. Przy decyzji, która z opcji jest bardziej prawdopodobna, na ocenę prawdopodobieństwa wpływa zbudowane w naszym umyśle wyobrażenie Doroty.
Rysunek 11: Dane z raportu Młodzi 2011 przedstawione za pomocą wykresu punktowego. Każda kropka odpowiada wartości, współrzędne kropki odpowiadają proporcji osób, które uznały daną wartość za istotną w życiu. Na osi OX przedstawione są odpowiedzi z badania z roku 1976, a na osi OY z badania z roku 2008. Takie zestawienie ułatwia porównanie nie bezwzględnych wartości, ale hierarchii ważności. Źródło: opracowanie własne
Zarządzanie niepewnością
Kolejnym problemem percepcji jest sposób, w jaki rozumiemy losowość i niepewność. Aby zilustrować, jak bardzo trudne to są pojęcia, zauważmy, że korzenie matematycznej teorii prawdopodobieństwa, oparte o rachunek kombinatoryczny, sięgają jedynie siedemnastego wieku. Za początki współczesnej teorii rachunku prawdopodobieństwa uważa się rok 1933, w którym Andriej Kołmogorow przedstawił jej aksjomaty w książce Foundations of the Theory of Probability Wcześniejsze rozumienie prawdopodobieństwa było intuicyjne i nieprecyzyjne.
Można zapytać, czy dla przeciętnego obywatela ważne jest zrozumienie niepewności? No cóż, w dobie powszechnych ubezpieczeń, zakładów losowych, zależności od giełdy można z całą pewnością powiedzieć, że rozumienie losowości i niepewności jest bardzo ważne. Zdają sobie z tego sprawę rządy krajów rozwiniętych, promując edukację swoich obywateli w tym kierunku. Świetnym przykładem, jak efektywnie taka edukacja może działać, jest profesor David Spiegelhalter. W roku 2007 otrzymał on pozycję profesora w obszarze społecznego i publicznego rozumienia ryzyka (ang. Professorship of the Public Understanding of Risk). Na różnych frontach (internet, publiczne prezentacje, książki) edukuje obywateli Wielkiej Brytanii na temat niepewności, zrozumienia ryzyka i innych tematów związanych z prawdopodobieństwem. Temat stał się bardzo ważny, gdy wina za spowodowanie kryzysu finansowego spadła na brak zrozumienia ryzyka. Zagadnienia, które porusza David Spiegelhalter, wykraczają poza ekonomię i często dotyczą tematyki medycznej (czynniki ryzyka a śmiertelność) i innych tematów. Współprowadzi on również bardzo ciekawy blog [David Spiegelhalter. Understanding uncertainty]
Oswajać się z niepewnością można na wiele sposobów, np. poprzez ciekawe zagadki. Przytoczmy jedną z takich zagadek.
W pewnym mieście są dwa szpitale. Duży, w którym urodziło się 100 niemowlaków i mały, w którym urodziło się 10 niemowlaków. Czy jest bardziej prawdopodobne, że odsetek chłopców przekroczył 60% w dużym czy w małym szpitalu?
Intuicyjne rozwiązanie jest następujące. Zwiększenie liczby urodzonych chłopców ponad standardowe 50% jest równie prawdopodobne w obu szpitalach. Ale w przypadku małego szpitala każdy pojedynczy chłopiec to 10% wszystkich porodów, przypadkowość wynikająca z tego, że pojawi się kilku chłopców więcej bardziej wpłynie na udział procentowy. W małym szpitalu jest większa szansa na 60% lub więcej chłopców, ponieważ do uzyskania tego wyniku wystarczy o jeden chłopiec więcej niż wynikałoby to ze średniego udziału chłopców wśród niemowlaków. W dużym szpitalu musiałoby się urodzić 10 chłopców więcej niż średnio.
Puenta z tej zagadki jest jednak taka, że możemy spodziewać się większej względnej losowości dla małych grup niż dla dużych. Jeżeli badamy pewną cechę na bazie określonej liczby pomiarów, to im mniej pomiarów, tym mniej dokładna ocena. Z jednej strony to całkiem oczywiste i zrozumiałe zjawisko, a z drugiej strony bardzo łatwo o nim zapomnieć.
Zilustrujemy to przykładem z polskiego podwórka. Spróbujemy przyjrzeć się zależności pomiędzy małymi klasami a wynikami w nauce. Z jednej strony małe klasy kojarzą się nam z większą dostępnością nauczyciela, który może poświęcić więcej czasu pojedynczemu dziecku. Z drugiej strony w dużych klasach dziecko ma szanse poznać rozwiązania rówieśników, a jeżeli rówieśników jest więcej, to może się nauczyć bardziej różnorodnych metod rozwiązywania zadań. Dzieci w naturalny sposób uczą się, podglądając sposób pracy rówieśników. Jak więc jest z tymi małymi klasami, czy są one lepsze czy gorsze?
sum(dbinom(60:100, 100, 0.5)) = 0.028 oraz P(Y ≥ 6) jako sum(dbinom(6:10, 10, 0.5)) = 0.376. Prawdopodobieństwo, że taka sytuacja wydarzy się w małym szpitalu jest około 13 razy większe niż, że w dużym
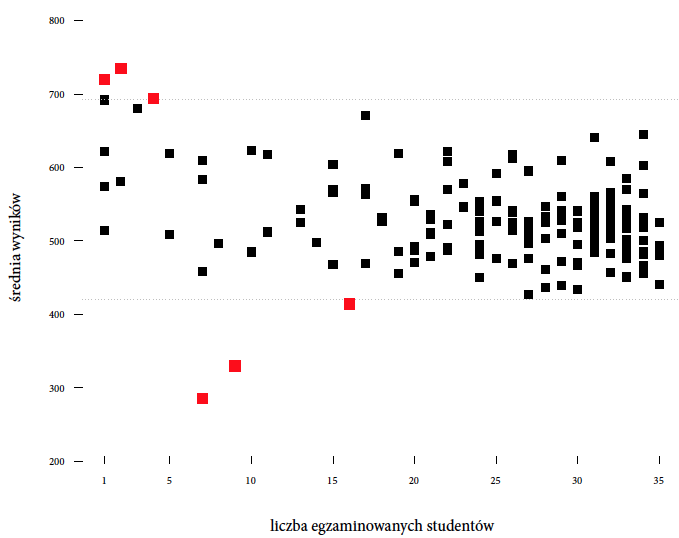
Rysunek 12: Wyniki z badania PISA 2012 dla Polski. Przedstawiony jest średni wynik szkoły z czytania ze zrozumieniem w zależności od liczby 15-letnich uczniów w szkole biorących udział w badaniu. Źródło: opracowanie własne
Nie odpowiemy na to pytanie bezpośrednio, pokażemy jedynie problem, z jakim mierzą się badacze, próbując na takie pytania odpowiadać. Przyjrzymy się danym zgromadzonym podczas badania PISA 2012 dla Polski. W roku 2012 w tym badaniu brały udział 184 szkoły, zobaczmy, które z tych szkół mają najlepsze wyniki z czytania ze zrozumieniem. Nie mamy informacji o wielkości klas, ale uwzględniając sposób losowania uczniów do badania, można założyć, że mniejsze klasy są w szkołach, w których w badaniu wzięło udział jedynie kilku uczniów.
Co się okazuje? Trzy najlepsze szkoły, czyli szkoły o najwyższych średnich, to szkoły, w których w badaniu udział wzięło tylko kilku uczniów, a więc szkoły o małych klasach i tylko jednej klasie w danym roczniku na szkołę. Czy jest to dowód, że małe klasy są lepsze? Okazuje się, że trzy najgorsze szkoły, a więc szkoły o najniższych średnich, to również szkoły mniejsze niż średnia (średnia wielkość uczniów na szkołę w tym badaniu to około 30 osób).
Można w tym miejscu szukać cech wspólnych dla trzech najlepszych lub najgorszych szkół, ale w tym przypadku uzasadnione jest stwierdzenie, że najbardziej skrajne szkoły to małe szkoły, ponieważ w małych szkołach zmienność wyników jest największa. Im większa szkoła i im więcej uczniów z tej szkoły bierze udział w teście, tym częściej średnia ze szkoły jest przeciętna. Warto o tym pamiętać, układając rozmaite rankingi szkół. Błędem byłoby przypisanie efektu małej próby jako zasługi dla wyjątkowych warunków edukacyjnych dla dziecka. Musimy uwzględnić, że średnia liczona z małej liczby osób ma tendencję do większych losowych fluktuacji. Te najlepsze wyniki dla małych szkół, podobnie jak najgorsze, mogą być związane wyłącznie z wyższą zmiennością w małych klasach.
Temat czynników wpływających na lepsze wyniki edukacyjne dzieci jest bardzo gorący. Rodzice często gotowi są do dużych inwestycji, aby tylko zapewnić dziecku dobrą edukację, i imają się wszelkich sposobów, by trafiło do jak najlepszej szkoły. Nic dziwnego, że artykuły dotyczące analizy czynników pozwalających na wybór szkoły są poczytne, a dyskusja czy lepsze są małe, czy duże klasy jest bardzo gorąca. W większości krajów na komfort małych klas pozwolić sobie mogą częściej prywatne szkoły, do których chodzą dzieci zamożniejszych rodziców, którzy z kolei są lepiej wyedukowani i mają większy dostęp do zasobów edukacyjnych. Jak więc wygląda efekt wpływu małych klas na wyniki edukacyjne dziecka, jeżeli uwzględni się też wszelkie czynniki związane ze statusem rodziców?
W książce [Steven Levitt and Stephen Dubner. Freakonomics: A Rogue Economist Explores the Hidden Side of Everything William Morrow, 2009] autorzy weryfikują dowody na wpływ różnych czynników związanych z rodzicami na wyniki szkolne dzieci. Upraszczając, pokazują oni, że czynniki, które mają wyraźny związek z wynikami, dzieci to czynniki określone jeszcze przed narodzeniem dziecka, takie jak wykształcenie rodziców czy zamożność. Czynniki związane z decyzjami rodziców, wybór lepszej szkoły, przeprowadzenie się do “lepszej” dzielnicy z “lepszymi” rówieśnikami, wczesne zajęcia dodatkowe, mają niewielki efekt jeżeli wpierw uwzględnić “efekt rodzica”. Niestety nasz umysł zapamięta te zależności, które możemy wykorzystać, nawet jeżeli ich efekt jest iluzoryczny.
Wielkość próby to tylko jeden z czynników wpływających na dokładność, z jaką można ustalić interesującą nas cechę. Posługując się ocenami we wnioskowaniu, warto uwzględnić niepewność, z jaką jesteśmy w stanie te oceny określić. Operowanie na niepewnościach to jednak słaby punkt naszego mózgu.
Ciekawa ilustracja tej trudności jest przedstawiona w książce [Ian Ayres. Super Crunchers: Why Thinking-By-Numbers is the New Way To Be Smart Bantam, 2008] przy okazji zestawienia ludzkiej intuicji z prostymi metodami statystycznymi, takimi jak regresja liniowa. Autor wykazywał, że olbrzymią zaletą jest również oszacowanie dokładności, z jaką wynik jest prognozowany.
Czy nasz mózg potrafi oceniać precyzję oszacowania? Nie bardzo. Aby to zilustrować, przedstawimy adaptację testu ze wspomnianej powyżej książki Super Crunchers. Poniżej przedstawiam dziesięć pytań. Zadanie polega na podaniu dla każdego z pytań takiego przedziału, że jesteśmy na 50% przekonani, że w danym przedziale znajduje się prawdziwa odpowiedź.
Jeżeli nie znamy dokładnej odpowiedzi na pytanie, to szacując ją, możemy podać wąski przedział, ryzykując, że będzie on za wąski i poprawna odpowiedź nie wpadnie do tego przedziału, możemy podać też przedział bardzo szeroki, by mieć pewność, że poprawna odpowiedź na pewno wpadnie do tego przedziału. Ale czy potrafimy zarządzać niepewnością tak, by za każdym razem podać przedział, do którego poprawna odpowiedź wpadnie na 50%?

Spróbuj Szanowny Czytelniku i sprawdź, czy udało Ci się podać przedziały, które pokryły poprawne odpowiedzi w mniej więcej pięciu przypadkach.
Jest to bardzo trudne zadanie. Co więcej, większość osób ma tendencje do zawyżania precyzji swoich oszacowań i budowania węższych przedziałów niż by należało. A co ciekawe, im bardziej uważamy się za dobrze poinformowanych, oczytanych, wyedukowanych, tym większą mamy tendencję, by uważać nasze szacunki za dokładne. Sokratesowskie Wiem, że nic nie wiem nie jest popularne w naszych czasach.
Jesteśmy przyzwyczajeni, by myśleć o informacjach w sposób zero-jedynkowy. Wiemy lub nie wiemy, wydarzy się lub nie wydarzy się, jest lepsza lub nie jest lepsza. Tymczasem w zadaniach wymagających oszacowań odpowiedzi stają się rozmyte. Wyniki badań może i lepiej wyglądają, jeżeli średni wynik przedstawimy z dokładnością do pięciu miejsc po przecinku, ale czy nie jest to mylące w sytuacji, gdy dokładność oszacowania tej średniej pozwala na określenie co najwyżej pierwszej cyfry po przecinku?
Ważniejsze od tego, co chciałeś pokazać, jest to, co zostało odczytane
Ponownie wracamy do obserwacji, że nie jest ważne, czy na wykresie przedstawione są dobre wielkości lub zależności, ale ważne jest, czy z wykresu poprawnie odczytamy te wartości czy zależności.
Sprawność w odczytywaniu informacji z wykresu jest silnie zależna od tego, jak często odbiorca obcuje z wykresami i jak bardzo jest wyćwiczony w odczytywaniu różnych wykresów. Projektując dla szerokiego odbiorcy, należy to wziąć pod uwagę. Warto przetestować czytelność opracowanej grafiki statystycznej na odpowiedniej grupie osób, by dowiedzieć się, co zauważyli, a czego nie zauważyli, jak wykres odczytali i jakie wyciągnęli z niego wnioski.