
Wykresy projektujemy po to, aby pokazywać historie ukryte w danych. Historie mogą być proste (np. w roku 2014 urodziło się więcej dzieci niż w roku 2013) lub złożone (liczba urodzonych dzieci jest związana ze strukturą demograficzną, jeden z czynników to boom demograficzny w okresie reprodukcyjnym wyżu demograficznego, do tego dochodzi ujemne saldo migracyjne). Im bardziej złożona historia, tym więcej wysiłku trzeba włożyć, by ją poprawnie i czytelnie przedstawić.
Do wyrażenia prostej historii nie potrzeba wykresu, w przypadku złożonej – już tak. Zilustrujmy to na przykładzie danych z Narodowego Spisu Powszechnego z roku 2011. Porównajmy trzy sposoby przedstawienia historii o liczebności i strukturze populacji w Polsce.
Opis słowny.
W wyniku przeprowadzenia Narodowego Spisu Powszechnego w roku 2011 ustalono, że w Polsce mieszka 38 511 800 osób, z czego 48,4% to mężczyźni, a 51,6% to kobiety.
Rysunek 1.
Tabela 2.
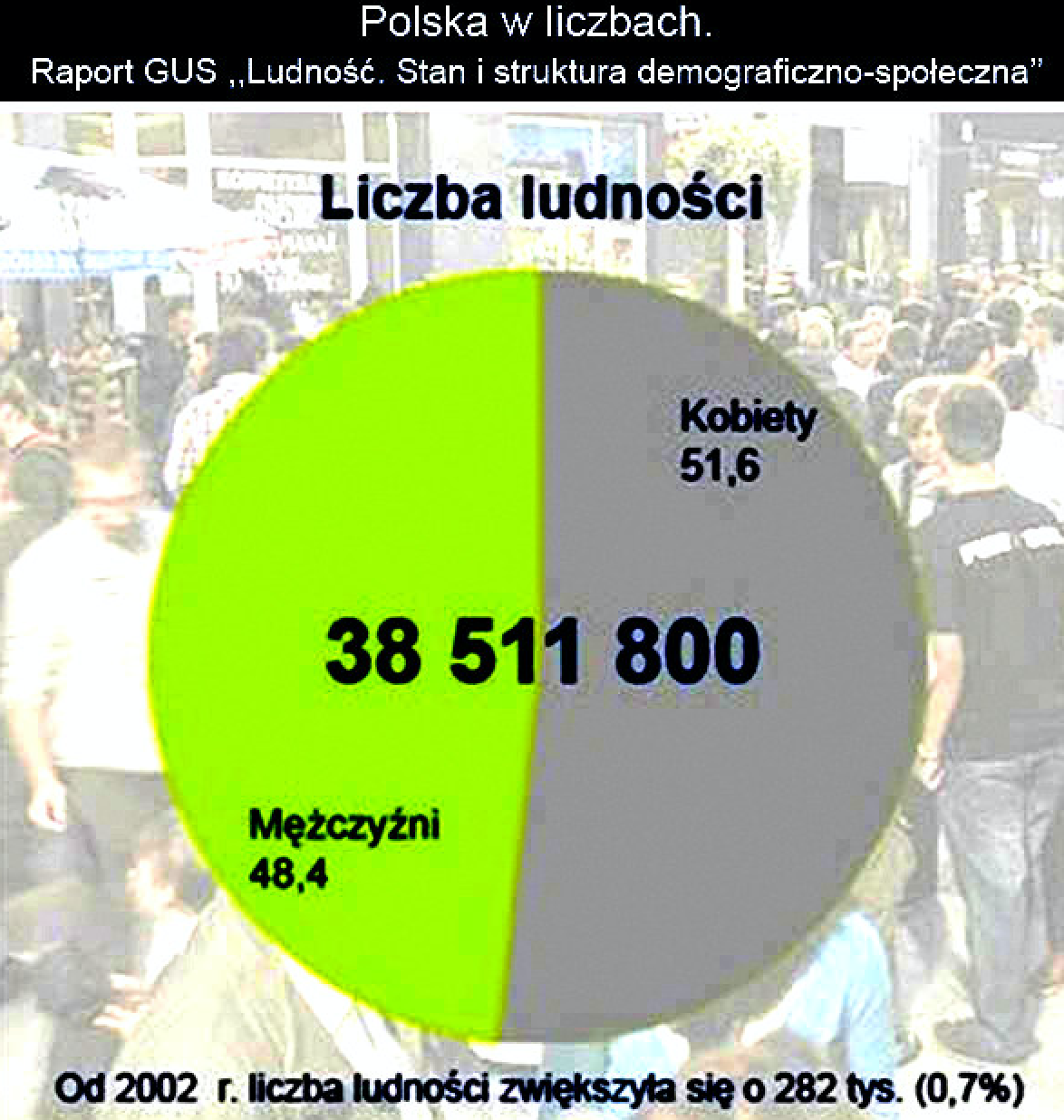 Rysunek 1: W Polsce mieszka 38 511 800 osób, z czego 48,4% to mężczyźni, a 51,6% to kobiety. Narodowy Spis Powszechny 2011. Źródło: Gazeta Wyborcza, http://bit.ly/1OBGZPb
Rysunek 1: W Polsce mieszka 38 511 800 osób, z czego 48,4% to mężczyźni, a 51,6% to kobiety. Narodowy Spis Powszechny 2011. Źródło: Gazeta Wyborcza, http://bit.ly/1OBGZPb
Czy potrzebujemy wykresu, aby pokazać trzy liczby? Czy wykres ułatwia ich zrozumienie lub wnosi dodatkową informację? Po dwakroć nie. Tabela ma wyraźną i łatwą do odczytania strukturę. Jedno zdanie słownego opisu komunikuje całą istotną informację. A wykres? Lubimy obrazki, ale jeżeli chodzi o przedstawianie informacji, to ten wykres nic nie wnosi.
Tabela 2: Wyniki z Narodowego Spisu Powszechnego z roku 2011
Zupełnie inaczej wygląda sytuacja, gdy mamy do przekazania złożony komunikat oparty na dużym zbiorze danych. Zobaczmy historię wyników polskich matur z lat 2010-2015. Porównajmy trzy poniższe sposoby prezentowania tej historii.
Opis słowny.
Wyniki matury z języka polskiego mają rozkład zbliżony do normalnego. W poszczególnych latach średnie tego rozkładu nieznacznie się różnią. Rozkład ten jest zaburzony w okolicy 21-22 punktów, czyli w pobliżu wartości stanowiących granicę zaliczenia (30% możliwych do uzyskania punktów). Praktycznie nie ma uczniów, którzy uzyskaliby jeden punkt poniżej progu zaliczenia, jest za to bardzo dużo osób, które zdały egzamin, otrzymując punkt więcej. Sugeruje to, że dosyć często osoby oceniające maturę, widząc, że do zaliczenia brakuje jednego–dwóch punktów, brakujące punkty “znajdowały”. W przypadku egzaminu z matematyki rozkłady są różne w różnych rocznikach i zdecydowanie nie przypominają rozkładu normalnego. W pobliżu progu zaliczenia również widzimy pewną nieregularność, największą w roku 2014. Jest ona jednak mniejsza niż w przypadku egzaminu z języka polskiego.
Rysunek otwierający ten esej.
Tabela 3.
Druga historia jest bardziej złożona. W tej sytuacji precyzja i struktura tabeli przepełnionej liczbami niewiele wnosi. Liczb jest zbyt wiele, by móc je w jakikolwiek sposób porównać, a i tak w tabeli 3 przedstawiono zaledwie jedną czwartą danych. Z kolei w opisie słownym mniej skupieni odbiorcy mogą się pogubić, z uwagi na jego długość. Nie jest on też kompletny, a zapoznanie się z nim trwa kilka–kilkanaście sekund. W tej historii wykres przedstawia dane z praktycznie tą samą dokładnością co tabela, ale można go szybciej odczytać.
Wykres czyta się zupełnie inaczej niż opis słowny. Tekst, czy to pisany czy mówiony, jest liniowy, jednowymiarowy. Wykres jest dwuwymiarowy i jako całość jest postrzegany jednocześnie. Nie ma początku ani końca. Dlatego komunikatów językowych nie można jednoznacznie przetłumaczyć na wykres, a wykresu nie sposób jednoznacznie wyrazić słowami.
Umiejętne zilustrowanie złożonej historii za pomocą wykresu pozwala na czytelniejsze i pełniejsze jej zaprezentowanie. Jednak budowanie i czytanie złożonych wykresów nie jest proste. Sprawność w posługiwaniu się językiem graficznym nie jest wrodzona i wymaga ćwiczeń oraz praktyki. Podobnie jak w przypadku nauki dowolnego języka ważne, by się z nim “osłuchać”. Można to uzyskać, oglądając dobrze zaprojektowane wykresy udostępnione w sieci lub przedstawione w innych esejach. Ale osłuchiwanie się nie wystarczy, aby w pełni opanować język. Ważna jest też umiejętność zauważania określonych reguł kompozycji wykresów, trzeba poznać gramatykę języka wizualizacji danych.
Po co nam gramatyka?
Czy słowa wystarczą, aby sprawnie się komunikować? Lingwista Daniel Everett twierdzi, że nie wystarczą. Do tworzenia bardziej złożonych komunikatów potrzebna jest gramatyka, i to wystarczająco bogata. Everett zasłynął z badań języka plemion Indian z Ameryki Południowej, szczególnie plemienia Pirahã. Zauważył, że gramatyka tego języka jest bardzo prymitywna, nie dopuszcza np. rekursji. Posługując się językiem Pirahã, nie można powiedzieć “Brat Jana ma dom”, trzeba użyć przynajmniej dwóch zdań: “Jan ma brata” i “Brat ma dom”. Przykład banalny, ale konsekwencje poważne. Wyniki Everetta wstrząsnęły światem lingwistów, stojąc w sprzeczności z teorią Noama Chomsky'ego o uniwersalnej bogatej gramatyce “wpisanej” w ludzki mózg. Czy umiejętność wyrażania komunikatów w postaci gramatyk rekursywnych jest wrodzona i typowa dla ludzi, czy też się ją nabywa?
gramatyka 1. zbiór reguł opisujących system języka
Tworzymy wykresy po to, by komunikować zależności obecne w danych. Spójrzmy więc na wykresy jak na zdania, które opisują zależności. Jakimi regułami rządzi się konstrukcja takich zdań? Kluczowe są dwa elementy.
Jeżeli użyjemy wystarczająco bogatego języka, to jednym zdaniem / jednym wykresem będziemy mogli przedstawić złożoną historię. Jeżeli posługujemy się prostym językiem, to do oddania tej samej treści będziemy potrzebowali wielu zdań/wykresów. Co więcej, zwiększamy ryzyko, że pewnych myśli w prostym języku nie da się wyrazić lub że po drodze zostaniemy źle zrozumiani.
Nie ma powodów, by przypuszczać, że umiejętność czytania wykresów jest wrodzona. Wiele osób ma trudności z interpretacją nawet prostych wykresów, co sugeruje, że jest to jednak umiejętność nabyta. Poświęcając czas na obcowanie z wykresami, uczymy się reguł ich konstruowania oraz reguł odczytywania znaczenia z wykresu.
Ten esej omawia gramatykę budowania wykresów, która została opracowana przez Hadleya Wickhama i zaimplementowana w bibliotece ggplot2 dla programu R Gramatyka ta jest oparta na bogatszej gramatyce, którą stworzył Leland Wilkinson, opisanej w książce The Grammar of Graphics. Z kolei gramatyka przedstawiona przez Wilkinsona bazuje na wynikach Jacquesa Bertina i jego pracy Sémiologie graphique. Korzysta też z rezultatów osiągniętych w bardzo wielu różnych dyscyplinach, od kartografii, sztuki przez badania percepcji i kognitywistykę po lingwistykę, matematykę i statystykę. Wizualizacja informacji to prawdziwie interdyscyplinarne zajęcie.
Nie jest naszym celem uczenie się jednego konkretnego narzędzia, ale poznanie bogatej i w miarę sformalizowanej struktury komponowania wykresów. Przykłady z użyciem biblioteki ggplot2 służą jedynie ilustracji omawianych zagadnień.
Osoby, które chciałyby głębiej poznać program R i pakiet ggplot2, mogą znaleźć wiele szczegółowych informacji w książce ggplot2: elegant graphics for data analysis. W języku polskim więcej informacji o programie R i bibliotece ggplot2 znajduje się w książce Przewodnik po pakiecie R.
Podobne zasady tworzenia wykresów dla języka Julia są zaimplementowane w pakiecie Gadfly, a dla języka Python w pakiecie ggplot
Dlaczego akurat gramatyka z pakietu ggplot2?
Wyróżniamy trzy rodzaje narzędzi do tworzenia wykresów wykorzystywanych przez osoby zawodowo prezentujące liczby.
Programy typu GIMP, Adobe Illustrator czy Inkscape.
Pozwalają na budowanie dowolnej infografiki. Wyobraźnia twórcy nie jest praktycznie niczym ograniczona, nawet danymi, które ma przedstawić. Można zbudować dowolny wykres, korzystając z dowolnych kształtów.
Narzędzia te nie tworzą połączenia pomiędzy danymi a elementami wykresu. To grafik decyduje, co, jak i dlaczego ma być przedstawione. W ten sposób na jego głowę spada dbanie o spójność i rzetelność prezentacji danych. Przy bardziej złożonych historiach łatwo jednak coś przeoczyć.
Pomysł na wyrażenie danych może być dowolny i ograniczony jest tylko pomysłowością artysty. Często jednak przerasta ona pomysłowość czytelników, którzy nie wiedzą, jak taki “artystyczny” wykres odczytać.
Programy typu Calc, Excel czy Tableau.
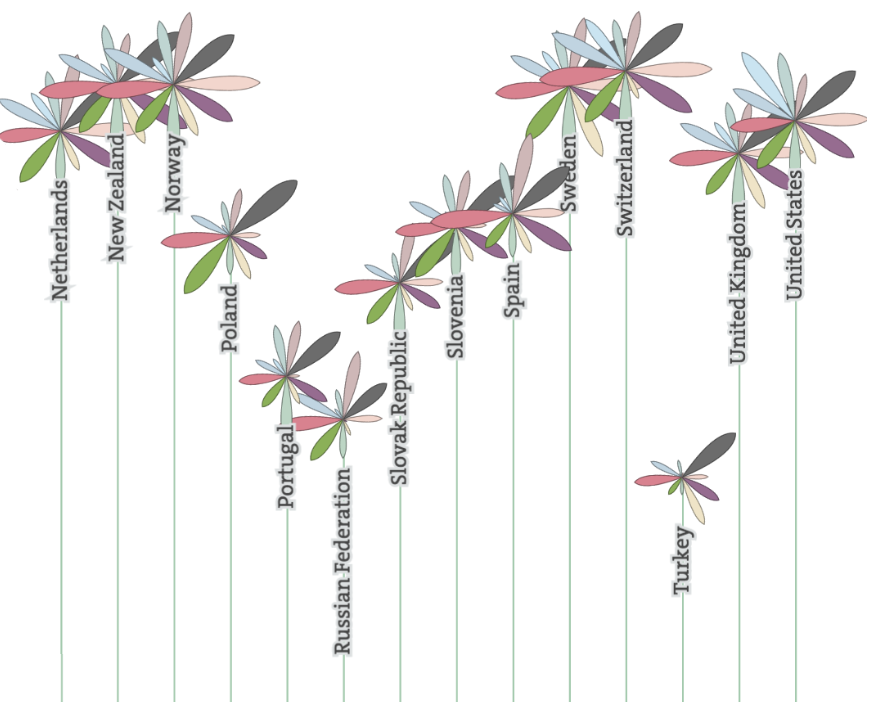 Rysunek 4: Wykresy przedstawiające składowe indeksu OECD Better Life Index. Oryginalna forma prezentacji danych
Rysunek 4: Wykresy przedstawiające składowe indeksu OECD Better Life Index. Oryginalna forma prezentacji danych
Pozwalają na szybkie tworzenie wykresów za pomocą zbioru szablonów. Szybkość jest tutaj kluczowym atutem. Użytkownik może błyskawicznie “wyklikać” szablon, wskazać kolumny w danych, które parametryzują szablon, i kolejny wykres gotowy.
To podejście pozwala na szybkie tworzenie wykresów, ale w dłuższej perspektywie może być ograniczające. Dostępnych szablonów może być wprawdzie bardzo dużo, ale jeżeli nie ma szablonu pasującego do naszej historii, to nie możemy ani prosto, ani szybko zbudować nowego.
Z reguły dostępne szablony nie są w stanie wyrazić złożonych historii. Zamiast jednego treściwego wykresu tworzy się kolekcje, “tablice rozdzielcze” pełne prostych wykresów, które można szybko budować i zestawiać.
Biblioteki języków programowania, takie jak ggplot2, oparte są o niewielkim zbiór cegiełek, które można elastycznie składać ze sobą w większe wykresy. Elastyczność jest tutaj słowem kluczem. Składanie elementów na wielu planach pozwala tworzyć złożone historie.
Wykres opisuje się jako związek atrybutów graficznych z danymi. Można zawsze odczytać, jakie dane określony atrybut graficzny wyraża, ponieważ reguły tworzące wykres określają znaczenie poszczególnych części wykresu.
W przypadku narzędzi pozwalających na szybkie “wyklikanie” wykresu ograniczeniem jest ich mała elastyczność. Gramatyka pozwala wyjść poza ograniczony zbiór szablonów tak zwanej nazwanej grafiki Z małych cegiełek możemy budować wielowarstwowe opisy przedstawiające złożone zależności w danych.
Ostatnie z wymienionych podejść charakteryzuje duży formalizm i wysoki próg wejścia, co dla niektórych stanowi wadę. Pamiętajmy jednak, że gramatyka języka wykresów jest związana ze sposobem, w jaki myślimy o zależnościach pomiędzy danymi. A formalizm tej gramatyki, gdy się go już opanuje, stanie się pomocą i oparciem, a nie przeszkodą.
W tym eseju, aby skrócić zapis, opisywana gramatyka języka wizualizacji danych określona jest słowem GrGramatyka. GrGramatyka nie tylko pozwala na tworzenie wykresów, ale też zmienia sposób, w jaki o nich myślimy. Gramatyka wymusza zauważanie w wykresach określonej struktury. Systematyzuje sposób ich odbioru. Ten trening umysłu posłuży nam na zawsze, bez względu na rodzaj narzędzi, jakich będziemy używać w przyszłości. GrGramatyka umożliwia rozkład logiczny wykresu na niezależne składowe. Każda z tych składowych pełni określoną funkcję. Schemat połączeń pomiędzy składowymi GrGramatyki przedstawiono na rysunku 5. Kolejne elementy tego schematu zostały omówione w kolejnych sekcjach.
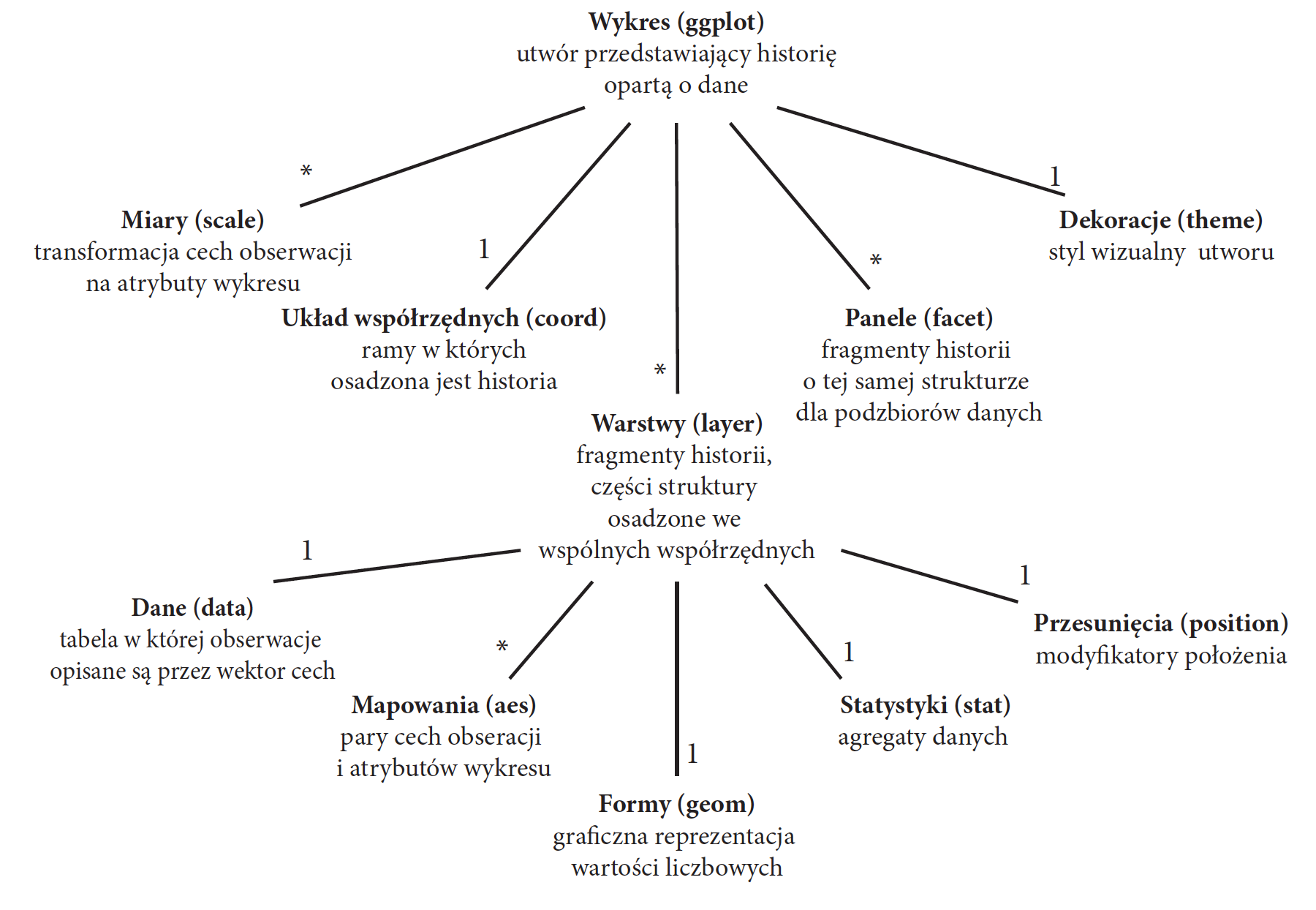 Rysunek 5: GrGramatyka języka wizualizacji danych, którą omawiamy w tym eseju. Wykres złożony jest z warstw (potencjalnie wielu), paneli, układu współrzędnych (zawsze jednego). Każda warstwa składa się z danych (jedno źródło), mapowań (potencjalnie wielu), form, statystyk itp.
Rysunek 5: GrGramatyka języka wizualizacji danych, którą omawiamy w tym eseju. Wykres złożony jest z warstw (potencjalnie wielu), paneli, układu współrzędnych (zawsze jednego). Każda warstwa składa się z danych (jedno źródło), mapowań (potencjalnie wielu), form, statystyk itp.
Dane
GrGramatyka pozwala na wyrażenie związku pomiędzy danymi a atrybutami graficznymi wykresu w sformalizowany sposób. Aby taki zapis był zwięzły i czytelny, musimy przyjąć dodatkowe założenia dotyczące struktury danych.
W ogólności dane mogą mieć najróżniejszą postać. Począwszy od tzw. danych niestrukturalnych, korpusów tekstu, plików multimedialnych, grafów, po dane w postaci tabeli, w której w kolumnach występują zmienne, a w wierszach obserwacje.
GrGramatyka zakłada, że dane znajdują się w tabeli, w tak zwanym wąskim formacie. Jeżeli dane zgromadzono w innej postaci, należy je wstępnie sprowadzić do postaci wąskiej.
O ile określenie postać tabeli nie wymaga dalszych wyjaśnień, o tyle zatrzymajmy się chwilę przy tym, co znaczy postać wąska. Rysunki 6 i 7 przedstawiają te same dane w postaci wąskiej i w postaci szerokiej.
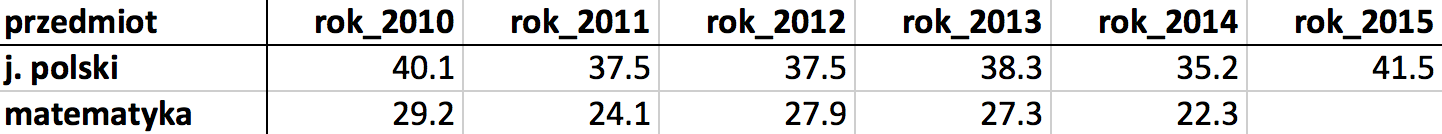
Rysunek 6: Reprezentacja szeroka danych. Średnie wartości dla różnych lat przedstawione są w różnych kolumnach
Rozważmy średnie wyniki egzaminu maturalnego z dwóch przedmiotów w podziale na lata. Na rysunku 6 widnieje szeroka reprezentacja danych. Wartości średnich odpowiadających różnym rocznikom są opisane w oddzielnych kolumnach. Rysunek 7 przedstawia te same dane w postaci wąskiej, wszystkie średnie znajdują się w jednej kolumnie.
Rozróżnienie na postać szeroką i wąską nie jest precyzyjne, gdybyśmy jednak chcieli opisać związaną z nim intuicję, to będzie ona następująca. W reprezentacji wąskiej każda zmienna jest opisana w jednej kolumnie. Jeżeli więc przyjmiemy, że interesuje nas zmienna średni wynik z matury, w reprezentacji wąskiej wszystkie wartości znajdziemy w jednej kolumnie. W przypadku reprezentacji szerokiej inną zmienną są średnie w roku 2010, a inną w roku 2012.
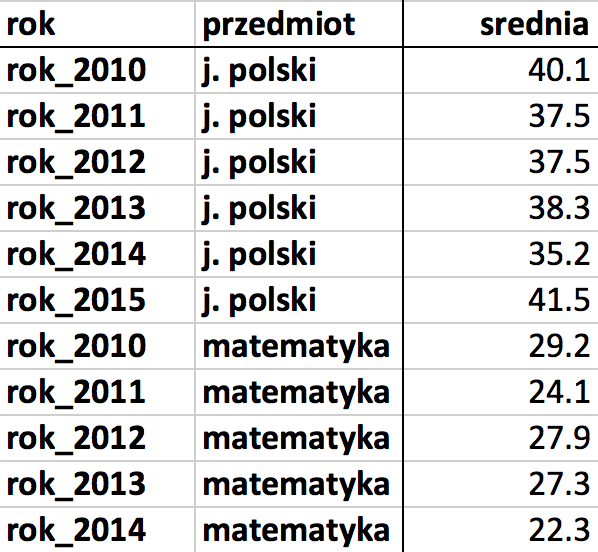 Rysunek 7: Reprezentacja wąska danych. Średnie opisane są w jednej kolumnie, a zmienne, mogące różnicować średnie, opisane są w pozostałych kolumnach
Rysunek 7: Reprezentacja wąska danych. Średnie opisane są w jednej kolumnie, a zmienne, mogące różnicować średnie, opisane są w pozostałych kolumnach
Przykłady zawarte w tym eseju oparte są na dwóch zbiorach danych. Pierwszy, częściowo przedstawiony w tabeli 8, dotyczy liczby urodzeń i zgonów w różnych krajach unormowanej na 1000 mieszkańców. Każdy wiersz opisuje jeden kraj, a kolumny zawierają współczynniki urodzeń, zgonów, populację i kontynent http://bit.ly/1Q3vheT}. Pomysł na wykorzystanie takich danych zapożyczyłem z książki “Grammar of Graphics” Lelanda Wilkinsona.
Drugi zbiór danych, którego wycinek znajduje się w tabeli 9, dotyczy danych z polskich matur z lat 2010-2015. Każdy wiersz opisuje jeden ucznio-egzamin, wyniki z egzaminu są w kolumnie punkty Dane pobrałem z użyciem pakietu ZPD udostępnionego przez Instytut Badań Edukacyjnych. Te dwa zbiory danych pozwolą nam omówić rozmaite cechy opisywanej GrGramatyki. Oba są dostępne w pakiecie SmarterPoland, odpowiednio pod nazwami countries i maturaExam
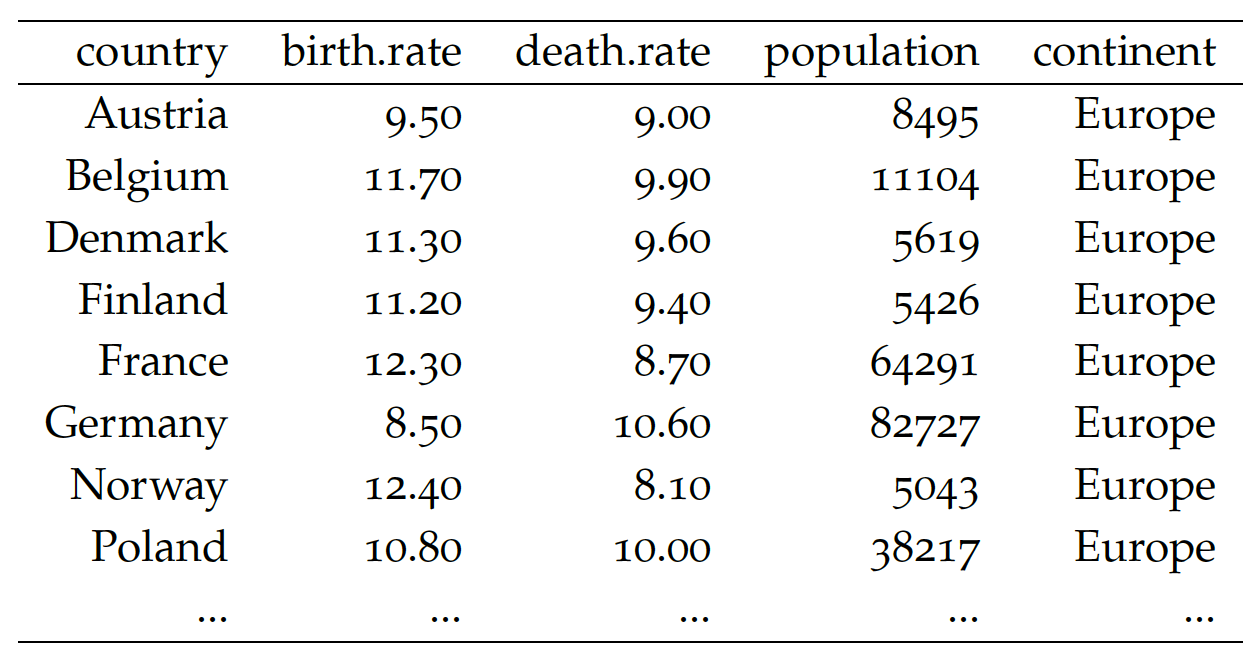
Tabela 8: Wybrane 8 wierszy ze zbioru danych
countries z pakietu SmarterPoland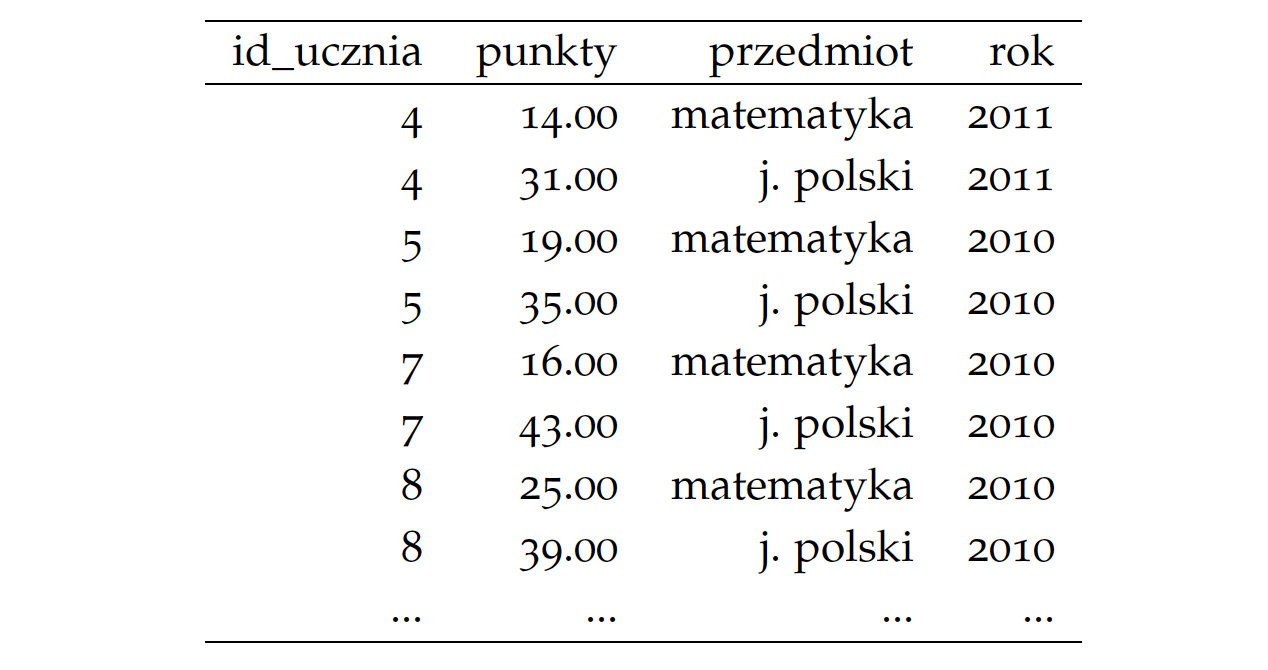
Tabela 9: Wybrane 8 wierszy ze zbioru danych
maturaExam z pakietu SmarterPolandWarstwy
Wyróżnikiem dobrej grafiki jest treściwa historia. Takiej historii nie opowiada się serią kilkudziesięciu podobnych wykresów. Powtarzalność i monotonia są zabójcze dla historii. Znacznie lepiej jest zebrać wszystkie wątki na jednym wykresie, w który można się zanurzyć i spokojnie go przeanalizować.
Jak komponować takie wykresy? Podobnie jak komponuje się muzykę, perfumy czy obrazy. Musimy rozplanować informację na uzupełniające się warstwy, przedstawiające dane z różnych perspektyw. Co ważne, warstwy powinny być osadzone we wspólnych ramach, dzięki czemu łatwiej jest je porównywać.
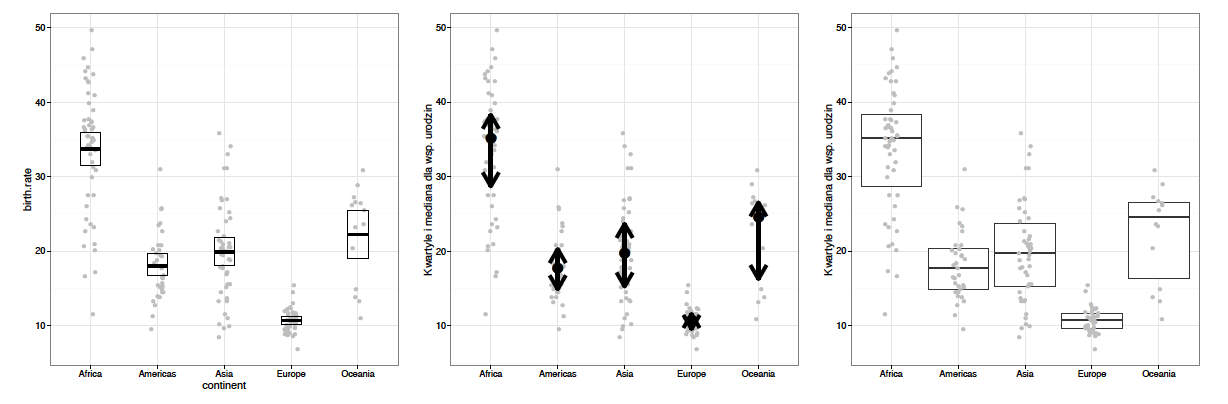
Czym różnią się poszczególne warstwy? Najczęściej poziomem szczegółowości/agregacji. Rysunek 10 przedstawia informację o współczynniku liczby urodzin w różnych krajach, z uwzględnieniem podziału na kontynenty. Wykres jest zbudowany z pięciu warstw, każda prezentuje inne ujęcie tej historii.
kompozycja
1. budowa utworu literackiego, muzycznego itp.; też: układ elementów tworzących jakąkolwiek estetyczną całość.
2. utwór lub jakakolwiek całość, w których poszczególne elementy są rozmieszczone i uporządkowane w określony sposób.
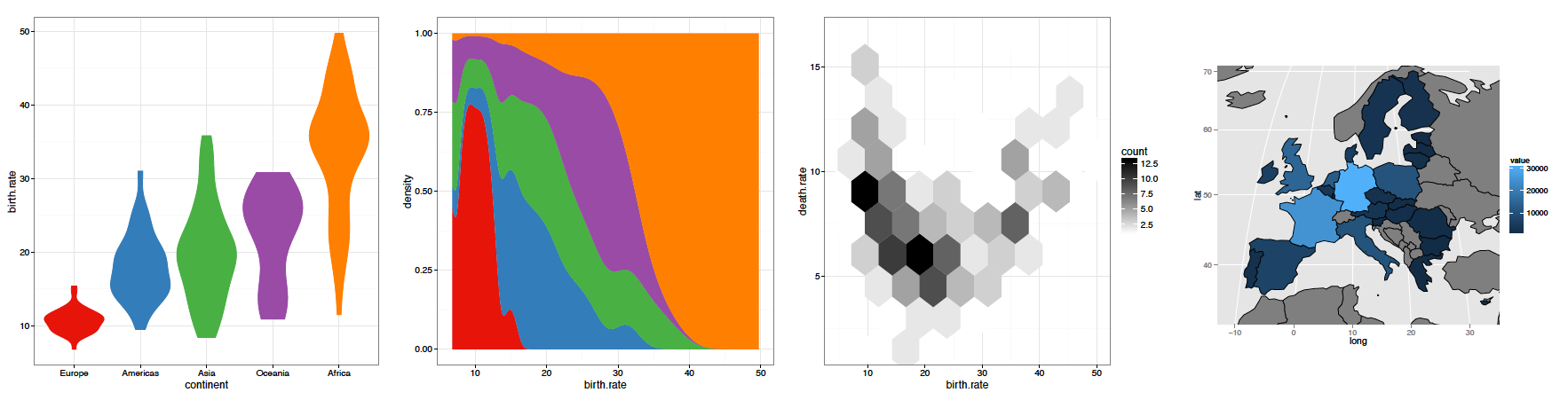
W pierwszej chwili oko skupia się na dużych plamach, w tym przypadku oznaczających rozkłady wartości. Na tym etapie łatwo zauważyć, że współczynnik narodzin w Europie jest znacznie niższy niż na innych kontynentach oraz że najwyższy jest w Afryce.
geom_violinKolejne pytanie, które się samo nasuwa, dotyczy typowych wartości tego współczynnika dla poszczególnych kontynentów. Połówkowe i ćwiartkowe statystyki dla każdego kontynentu zostały tutaj oznaczone czerwonymi pudełkami, a wartości skrajne można odczytać, analizując kropki. Daje to możliwość dokładniejszego porównania Ameryk, Azji i Oceanii.
geom_crossbar przedstawia medianę i kwartyle, rzez co pudełko obejmuje 50% środkowych wartościUstaliwszy porządek pomiędzy kontynentami, możemy zejść krok głębiej i porównać wartości dla poszczególnych krajów. Okazuje się, że w Afryce znajdziemy państwa o bardzo niskiej dzietności, ale w Europie nie istnieje kraj o dzietności choćby zbliżonej do typowej na innych kontynentach.
geom_jitter przedstawia dane za pomocą kropek, osobno dla każdego kraju, co ułatwia to identyfikacje wartości skrajnych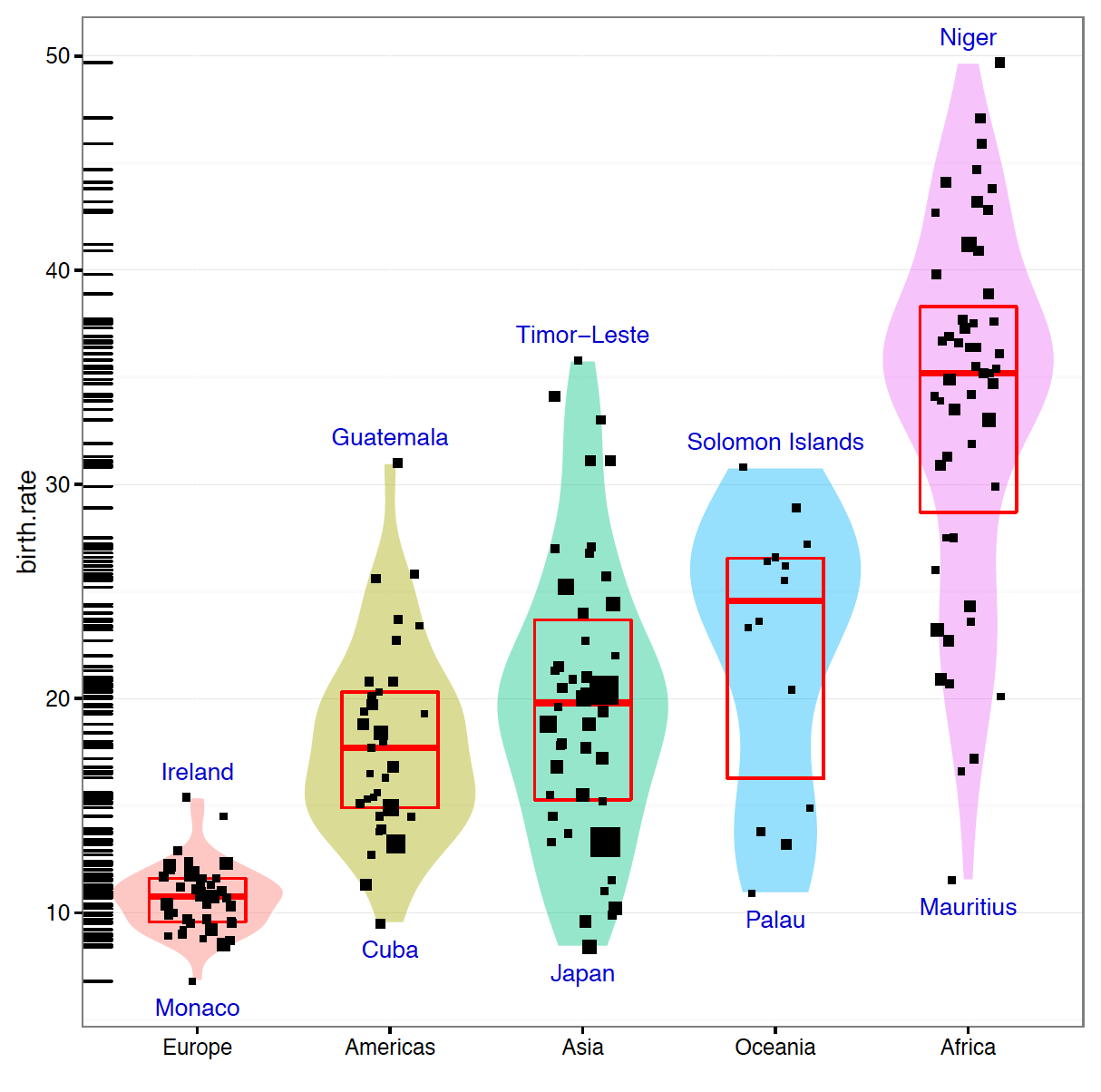
Każda z warstw przedstawia pewien aspekt niewidoczny na innych warstwach, przez co razem wzajemnie się uzupełniają. Ten wykres jest przeładowany informacją, a jednak przyjemniej jest go studiować, niż oglądać każdą warstwę osobno. Definicja wykresu 10 wygląda następująco.
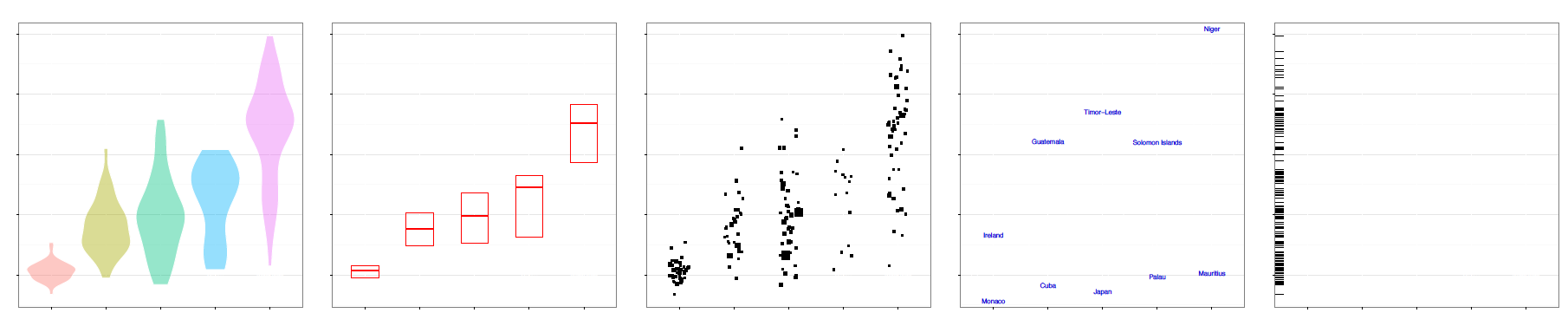
Rysunek 10: Wykres na górze składa się z pięciu warstw, które zostały zaprezentowane w kolejnym wierszu. Wszystkie warstwy opisują częstość urodzeń w różnych krajach w rozbiciu na kontynenty. Kolejne warstwy przedstawiają: (1) rozkład cechy dla kolejnych kontynentów za pomocą wykresu skrzypcowego – widać obszary największego natężenia, nie widać wartości połówkowych, (2) medianę i kwartyle dla każdego z kontynentów z osobna – widać wartości połówkowe i ćwiartkowe, nie widać całego rozkładu, (3) każdy kraj jako osobna kropka – łatwo zidentyfikować wartości skrajne, nie widać dobrze natężenia, (4) nazwy skrajnych krajów, (5) wartości dla każdego z państw za pomocą kresek przy osi
ggplot(countries, aes(x=continent, y=birth.rate)) + geom_violin(aes(fill=continent)) + geom_crossbar(fun.data = "q3", color="red") + geom_jitter(position=position_jitter(width = .45)) + geom_text(aes(label=country), color="blue3") + geom_rug(sides = "l")
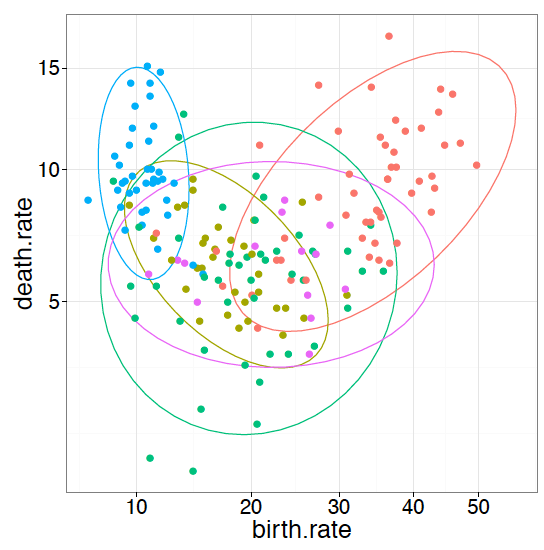
Wykres 11 przedstawia te same dane, ale z innej perspektywy. Zestawia on informację o współczynniku narodzin z informacją o współczynniku zgonów. Obie te miary, wyrażone w tych samych jednostkach (urodzenia/zgony na 1000 osób), pozwalają łatwiej zrozumieć, co się dzieje w populacjach poszczególnych krajów. Również ten wykres składa się z kilku warstw, które się wzajemnie uzupełniają.
R odtwarzające przedstawione tutaj wykresy znajdują się na stronie http://bit.ly/1OpCyWZ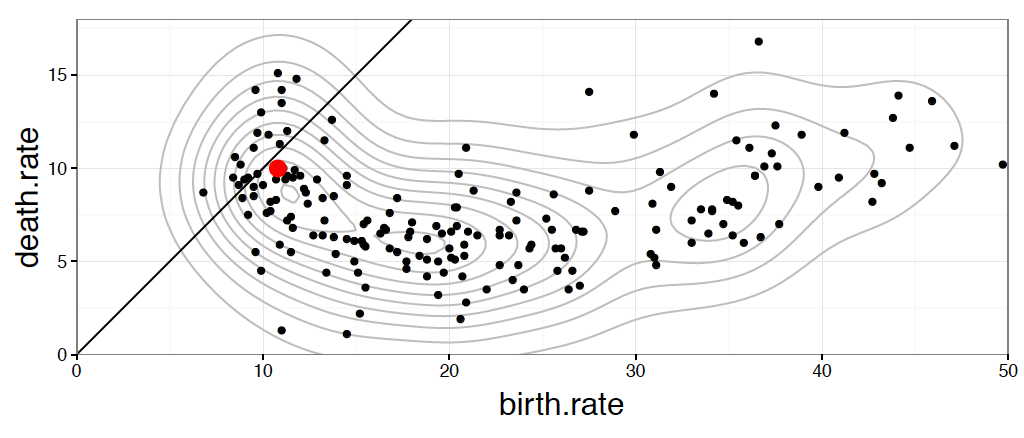
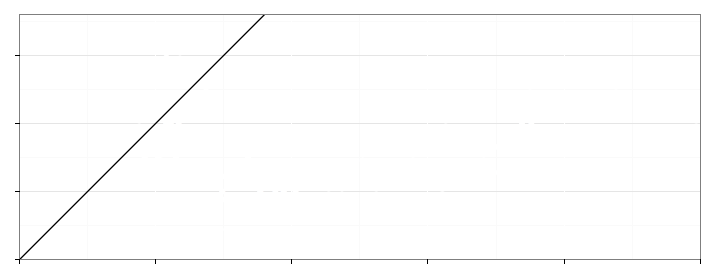
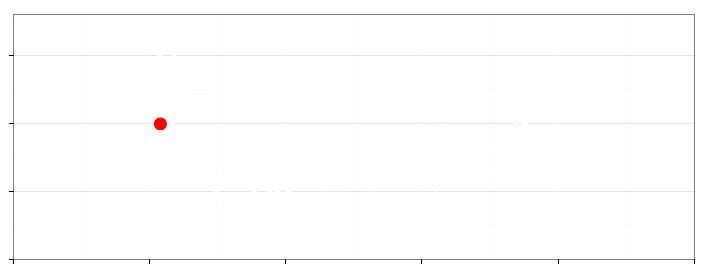
Rysunek 11: Wykres na górze strony składa się z czterech warstw, które zaprezentowano w osobnych wierszach. Kolejne warstwy przedstawiają: (1) każdy kraj jako osobna kropka, (2) informację o zagęszczeniu krajów przekazaną za pomocą konturów, (3) prostą $y=x$, określającą równość współczynnika urodzeń i zgonów, (4) wyróżniona jedna kropka odpowiadająca współczynnikom dla Polski
Najbardziej rzucającą się w oczy warstwą są kontury. Ułatwiają one identyfikację trzech skupisk: krajów o bardzo wysokim współczynniku urodzeń i średnim współczynniku zgonów (głównie kraje z Afryki), krajów o średnim współczynniku urodzin i niskim współczynniku zgonów (głównie kraje z Azji i Ameryk) oraz krajów o bardzo niskim współczynniku urodzin i średnim współczynniku zgonów (starzejące się kraje Europy).
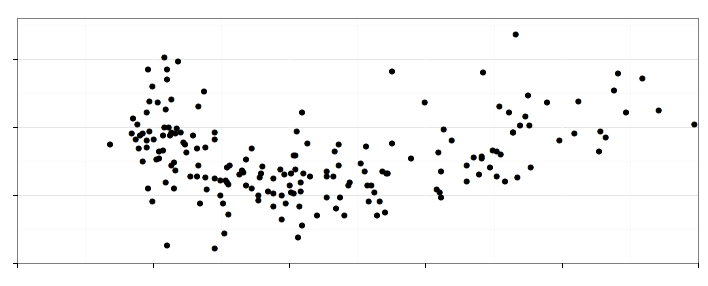
Uzupełnieniem poziomic jest warstwa przedstawiająca współczynniki dla każdego kraju za pomocą kropek. Pomaga to odnaleźć państwa o skrajnych wartościach współczynników.
Trzecia warstwa nie zależy od danych, ale ułatwia interpretację. Pokazuje ona linię, wzdłuż której jest tyle samo urodzin co zgonów. Kraje na lewo od tej linii charakteryzuje większa liczba zgonów niż urodzin, a kraje na prawo – więcej urodzin niż zgonów.
Ostatnia warstwa wyróżnia wartości dla Polski. Większa kropka, oznaczona rzucającym się w oczy kolorem, pozwala na szybką identyfikację parametrów naszego kraju i odniesienie go do pozostałych.
W omawianej GrGramatyce każda warstwa jest opisana przez cztery składowe: dane, na których została zbudowana, mapę kodowania danych na cechy wykresu, formę graficzną oraz statystykę użytą do transformacji danych. W kolejnym punkcie został omówiony mechanizm mapowania.
Mapowania/kodowanie
Nieodłącznym elementem wykresu są dane. Najczęściej jednak dane liczbowe nie są przedstawione wprost. Na wykresach nie umieszcza się liczb, ale pokazuje się te liczby za pomocą atrybutów elementów wykresu. Dobre skomponowanie wykresu polega na czytelnym zakodowaniu danych za pomocą elementów wykresu, tak by odbiorca, po pierwsze, wiedział, czy dany element jest ważny, czy nie, a po drugie, by potrafił odczytać związaną z tym elementem wartość.
O jakie elementy chodzi? Na potrzeby tej części opowieści przyjmijmy, że chcemy przedstawić współczynnik urodzeń i zgonów w różnych krajach za pomocą zbioru kropek, tak jak na rysunku 11. Każda kropka jest opisana przez współrzędne, kolor, wielkość, obrót itp. Takich możliwych charakterystyk kropki można wymyślać wiele. Kodowanie to przepisanie danych na charakterystyki elementów wykresu.
Im więcej zmiennych chcemy zaprezentować na wykresie, tym więcej charakterystyk – atrybutów graficznych musimy wykorzystać. Nie każde kombinacje atrybutów mogą być zastosowane jednocześnie. Ważne jest, by cechy były kodowane ortogonalnie, a więc by można je było niezależnie odczytać.
Przykład z rysunku 12 pokazuje, że takie pary jak kształt i kolor można bez problemu niezależnie rozkodować, ale już kombinacji kształtu i stopnia obrotu nie można. Czy trójkąt skierowany w dół to obrócony trójkąt skierowany w górę, czy zupełnie nowy symbol? Jak zatem wybierać dobre, ortogonalne zbiory atrybutów? Różni autorzy proponują różne zestawy atrybutów graficznych.
Najszerszą listę przedstawił Jacques Bertin w “Semiologii grafiki”. Między innymi wyróżnił on fakturę, gęstość kreskowania i kierunek kreskowania. Ale już Leland Wilkinson w swojej książce o gramatyce grafiki krytykował niektóre z propozycji Bertina, np. kwestionował użyteczność faktury. W opisywanej tutaj GrGramatyce Hadley Wickham zdecydował się na wskazanie siedmiu w miarę ortogonalnych atrybutów kropek.
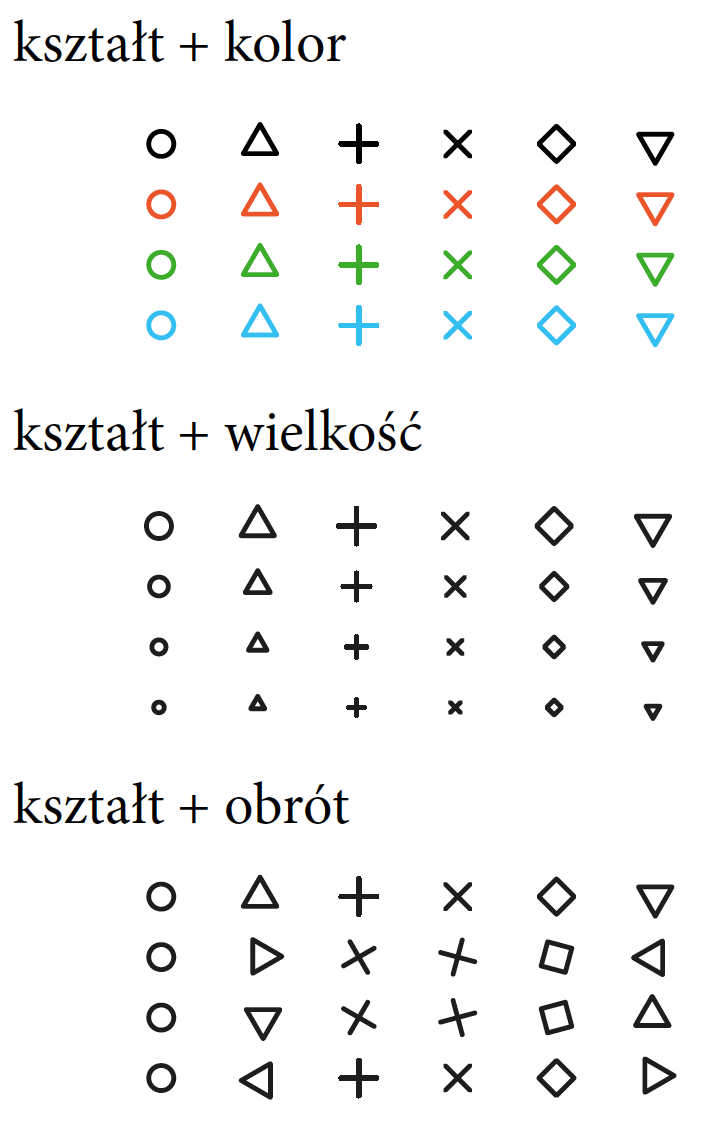 Rysunek 12: Nie każde cechy mogą być odczytywane niezależnie. Przykładowo kształt kropki i obrót. Dla pewnych kształtów nie można odczytać wartości obrotu
Rysunek 12: Nie każde cechy mogą być odczytywane niezależnie. Przykładowo kształt kropki i obrót. Dla pewnych kształtów nie można odczytać wartości obrotu

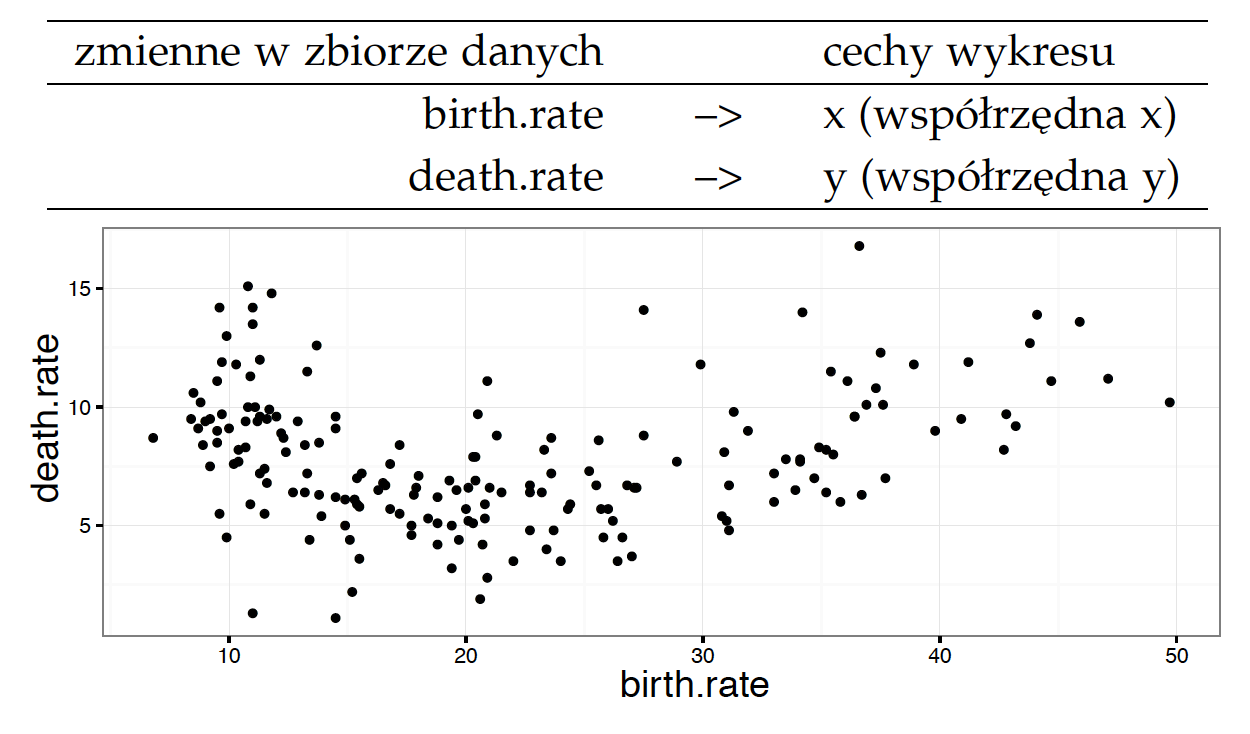
Mamy więc wyróżnione cechy elementów wykresu, na które możemy mapować wartości liczbowe. Jak takie mapowanie wygląda? Przedstawmy je na przykładzie. Zacznijmy od dwóch podstawowych cech kropek: współrzędnych x i y. Na rysunku 14 przedstawiono wykres, na którym współrzędne kodują informację o zmiennych częstość narodzin i częstość zgonów.
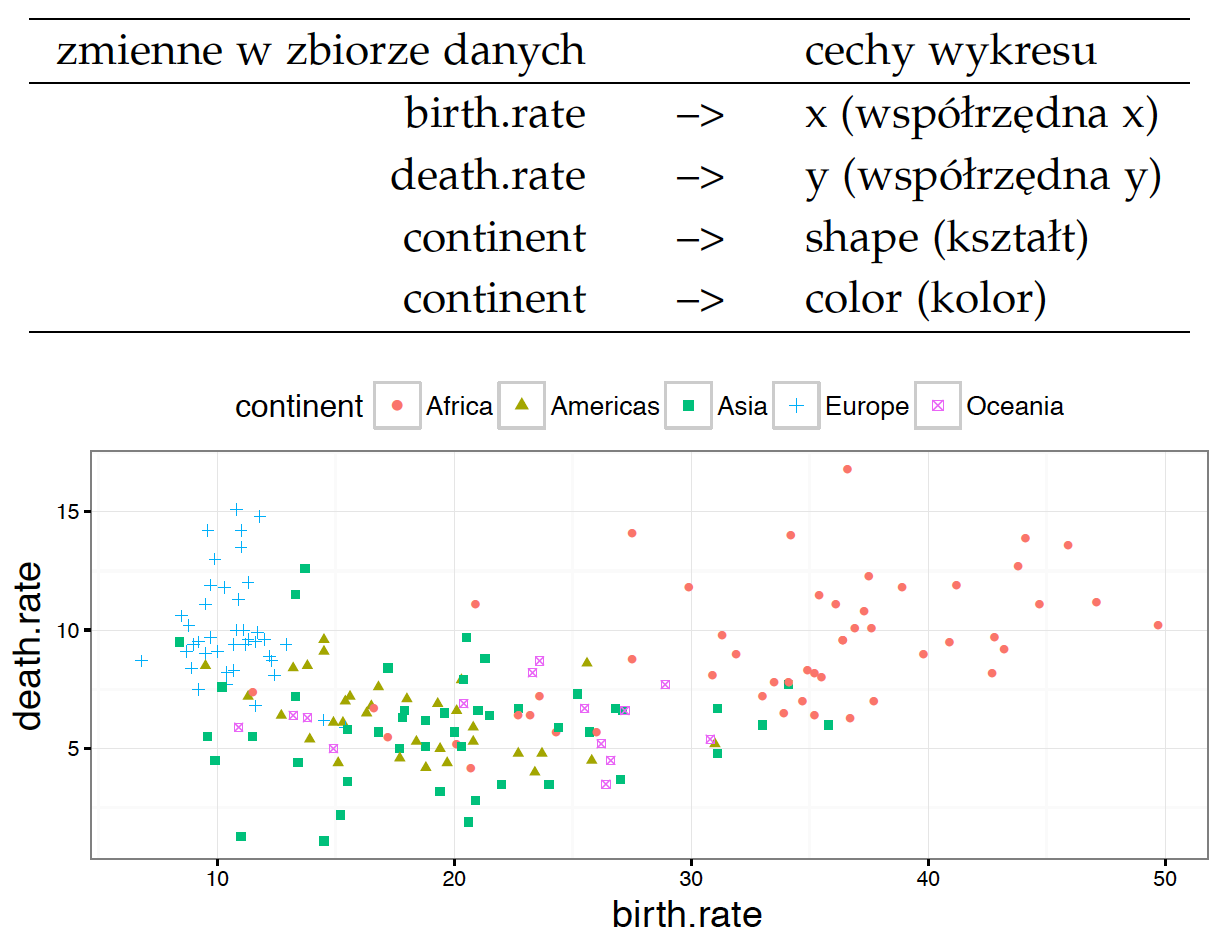
Przyjmijmy, że chcemy teraz dodać kolejną zmienną do wykresu, np. informację o tym, na którym kontynencie położone są poszczególne kraje. Aby taką informację zakodować, musimy wskazać kolejny atrybut, który będzie odpowiadał wartościom zmiennej kontynent.
Rysunek 13: Atrybuty graficzne kropek zgodnie z GrGramatyką
Dwie najczęściej wykorzystywane charakterystyki to kolor i kształt. Zastosujmy je obie, aby dodać informację o kontynencie. Wynik takiego kodowania został zaprezentowany na wykresie 15. Jedna zmienna może być przedstawiona za pomocą kilku atrybutów wykresu, ale jeden atrybut może odpowiadać tylko jednej zmiennej.
Rysunek 14: Wykres kropkowy / wykres rozproszenia, który przedstawia dwie zmienne, za pomocą współrzędnych x i y. Oba atrybuty można odczytać niezależnie od siebie, pomocne są w tym osie wykresu
Zakodowanie tej samej zmiennej przy użyciu kilku atrybutów jest przez niektórych minimalistów uznawane za błąd. Wprowadza bowiem dodatkowe elementy do wykresu, nie przekazując żadnej dodatkowej treści i duplikując już dostępną informację. Jeżeli jednak naszym celem jest wzmocnienie widoczności określonej zmiennej, to podwójne kodowanie może w tym pomóc.
W kolejnym kroku zakodujemy dodatkowo informację o populacji poszczególnych krajów. Który atrybut się do tego najbardziej nadaje? W przypadku wielkości populacji naturalnym wyborem jest wielkość kropki, ponieważ wiąże się z nią natychmiastowe skojarzenie: większa kropka – większa populacja. Dodatkowo użyjmy też do tego celu koloru, z ciemniejszym kolorem oznaczającym większą populację.
Wykres 16 rozszerza poprzedni o dodatkową informację. Widzimy jednak, że przy tej gęstości informacji coraz trudniej precyzyjnie odczytać poszczególne atrybuty.
Rysunek 15: Wykres kropkowy, który przedstawia trzy zmienne za pomocą czterech atrybutów kropek: współrzędnych x i y, koloru i kształtu. Każdy z tych atrybutów można odczytać niezależnie, dla współrzędnych jest to możliwe dzięki osiom, dla koloru i kształtu – dzięki legendzie. Kolor to silny wyróżnik, a dodanie dodatkowo kształtu pozwala lepiej rozróżniać podobne do siebie kolory
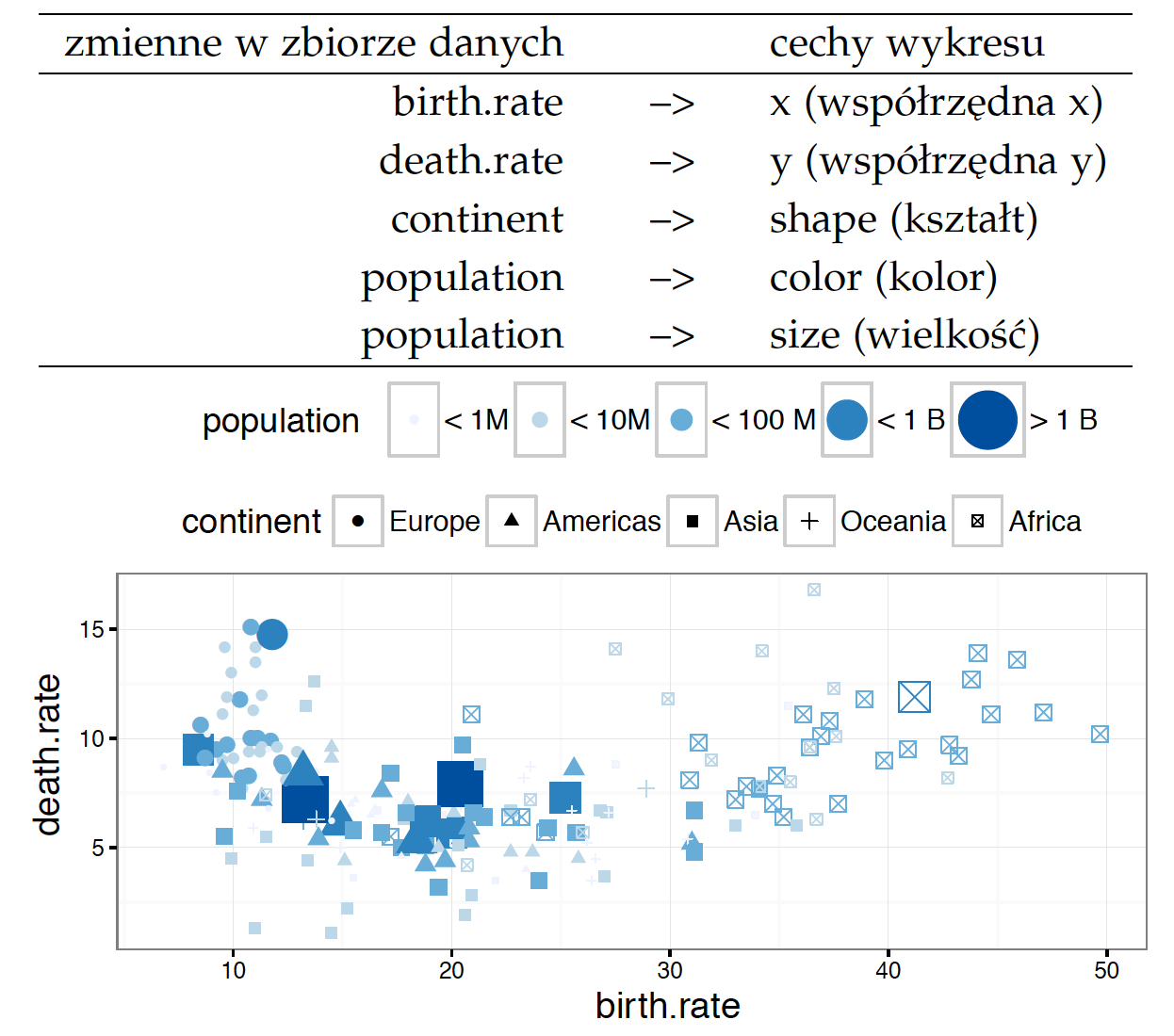
Zwróćmy uwagę na różnice w kodowaniu kolorów pomiędzy wykresem 15 a 16. Gdy kolor kodował zmienną jakościową continent, wybrane były dobrze rozróżnialne kolory. Gdy zaś kolor kodował zmienną ilościową population, wybrana została gradacyjna skala kolorów.
Mapowanie zmiennych liczbowych na atrybuty wykresu to kluczowe operacje w GrGramatyce. Nie musimy się domyślać, w jaki sposób zakodowane są dane. Do każdego mapowania dodawana jest informacja, jak odczytać atrybuty wykresu – umieszczona zostaje albo na osiach (dotyczy współrzędnych), albo w legendzie (wielkość, kolor, kształt). Pomimo że można by wymyślać wiele dodatkowych atrybutów kropek, widzimy, że już przy pięciu różnych trudno je precyzyjnie odczytać.
Rysunek 16: Wykres kropkowy przedstawiający cztery zmienne za pomocą pięciu atrybutów kropek, które mogą być niezależnie odczytane: współrzędnych x i y, koloru, kształtu i wielkości. Kształt i kolor można odczytać niezależnie od siebie, są to cechy ortogonalne. Jednak już wielkość kropki nie jest tak prosta do odczytania. Nawet dla pięciu różnych wielkości zamieszczonych w legendzie nie jest oczywiste, jak odróżnić trzy największe spośród nich, a dodatkowe problemy sprawiają kropki różnych kształtów. Kwadraty wydają się większe niż koła, a koła większe niż krzyżyki
Definicja wykresu 16 wygląda następująco.
ggplot() + geom_point(data=countries, aes(x=birth.rate, y=death.rate, shape=continent, color=population, size=population))
Mapowania określają sposób kodowania zmiennych na atrybuty graficzne. Każda warstwa wykresu może być uformowana przez inne elementy graficzne, a różne elementy graficzne mogą kodować dane za pomocą różnych atrybutów. Dlatego w kolejnym kroku zostały omówione różne formy graficzne.
R odtwarzające przedstawione tutaj wykresy znajdują się na stronie http://bit.ly/1YUkbQUFormy/geometrie
W opisywanej GrGramatyce wykres złożony jest z warstw. Na warstwę składa się zbiór danych, kodowanie zmiennych, definicje statystyk i przede wszystkim forma, która określa wygląd elementów warstwy. W zależności od użytych form prezentacja danych może być bardziej lub mniej czytelna, estetyczna lub nieestetyczna, interesująca lub nieinteresująca.
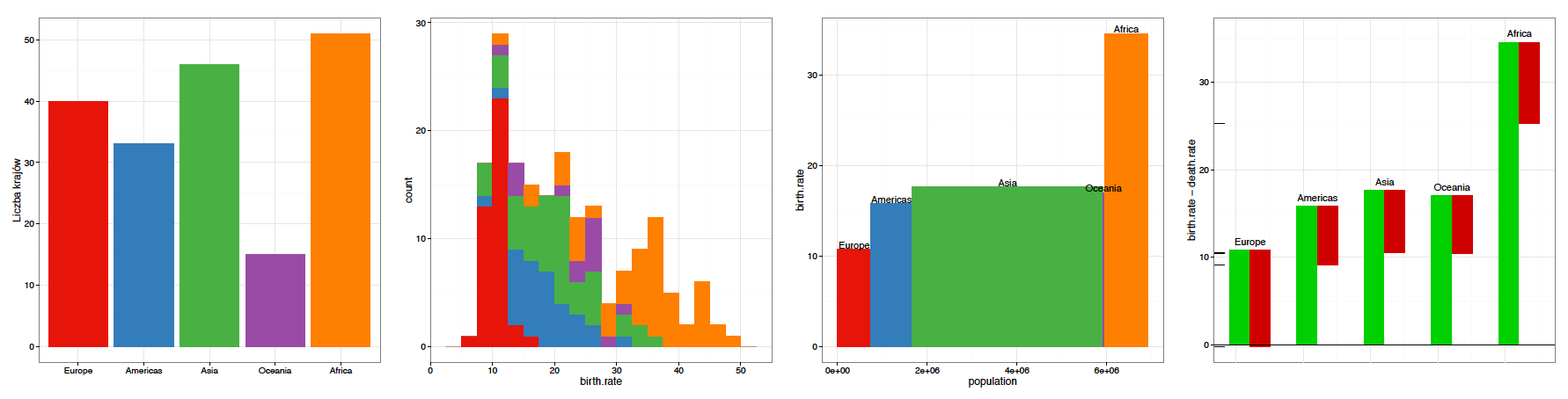 Rysunek 17: Wykorzystując prostokąty, możemy przedstawiać dane na różne sposoby
Rysunek 17: Wykorzystując prostokąty, możemy przedstawiać dane na różne sposoby
Prostokąty są jedną z form najchętniej wykorzystywanych na wykresach. Najczęstszym sposobem użycia prostokątów jest ustawienie ich obok siebie, zaczepionych w jednym miejscu i różniących się tylko długością. Taki wykres pozwala na zakodowanie jednej zmiennej za pomocą długości słupków, być może drugiej zmiennej za pomocą uporządkowania słupków i ewentualnie kolejnej zmiennej za pomocą koloru wypełnienia.
Pomimo iż zazwyczaj wykorzystywana jest tylko długość prostokątów, to ich użycie umożliwia zakodowanie danych również za pomocą szerokości, położenia lub pola. Daje to szerokie możliwości wyrażania danych. Kilka przykładów przedstawiono na rysunku 17. Należy być jednak ostrożnym, by zbytnio nie udziwnić wykresu, tak by odbiorca nie miał trudności z jego odczytaniem. Poniższa tabela przedstawia korzyści i wady zastosowania prostokątów.
Inną często wykorzystywaną formą na wykresach są kropki. Położenie każdej kropki koduje dwie zmienne. Zbiór kropek tworzy chmurę, a na podstawie kształtu chmury kropek można wnioskować o zależnościach pomiędzy zmiennymi. Przypomina to co prawda trochę zajęcie augurów, rzymskich kapłanów, ale przy odrobinie wprawy można identyfikować wartości odstające, skupiska kropek oraz rodzaj i siłę zależności.
geom_bar, a formę w której można określić i położenie i szerokość i długość prostokątów nazywa się geom_rect
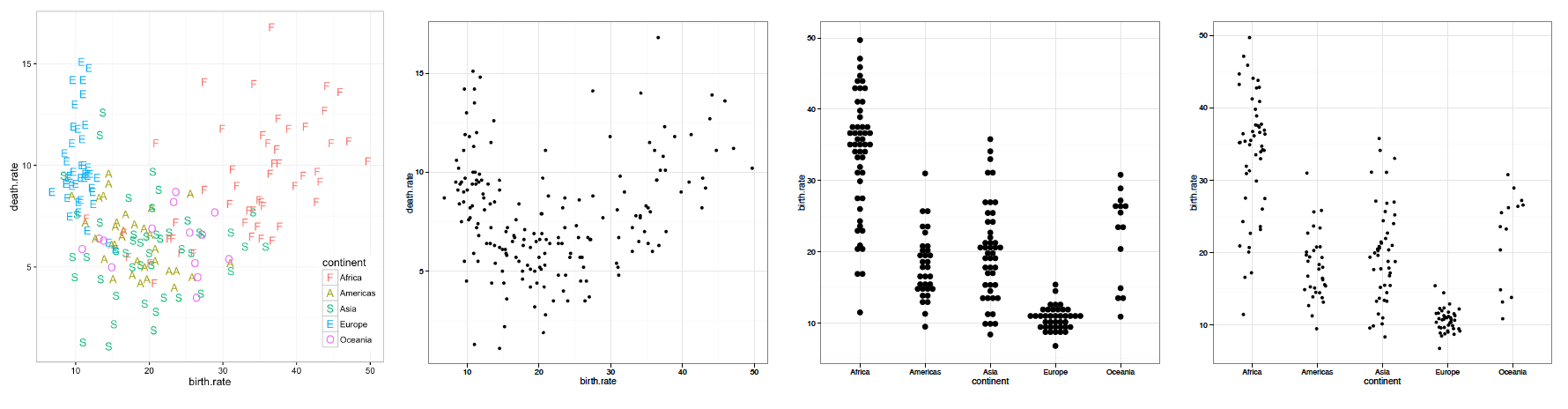 Rysunek 18: Prezentacja danych z użyciem kropek. W każdym przypadku jedna kropka to jeden kraj. Prezentacja różni się jednak w zależności od wariantu zastosowanej formy oraz kodowanych zmiennych
Rysunek 18: Prezentacja danych z użyciem kropek. W każdym przypadku jedna kropka to jeden kraj. Prezentacja różni się jednak w zależności od wariantu zastosowanej formy oraz kodowanych zmiennych
Przedstawianie danych za pomocą kropek pozwala na wykorzystanie dodatkowych charakterystyk kropek, które są ortogonalne w stosunku do położenia, takich jak kolor, wypełnienie, kształt, wielkość, stopień przezroczystości. Na rysunku 18 pokazane są te same dane z zakodowaną dodatkową cechą – czy to poprzez kolor, czy wielkość kropki, czy też kształt. Każdy z tych kanałów można odczytać niezależnie, a zatem istnieje możliwość zaprezentowania dodatkowej zmiennej za pomocą koloru, a innej za pomocą wielkości lub kształtu. Poniższa tabela przedstawia wady i zalety stosowania kropek.
O ile kropki świetnie nadają się do prezentacji niezależnych obserwacji, o tyle w wizualizacji par lub zbiorów zależnych obserwacji dobrze sprawdzają się linie, ścieżki i odcinki. W przypadku takich obiektów mamy do czynienia z dodatkowym atrybutem graficznym, takim jak grupa. Obserwacje o tej samej wartości zmiennej grupującej będą połączone odcinkami/ścieżką. Odcinkom możemy nadawać takie właściwości jak kolor, przezroczystość, grubość, typ linii. Na rysunku 19 zobrazowano różne wykorzystanie odcinków do prezentacji danych.
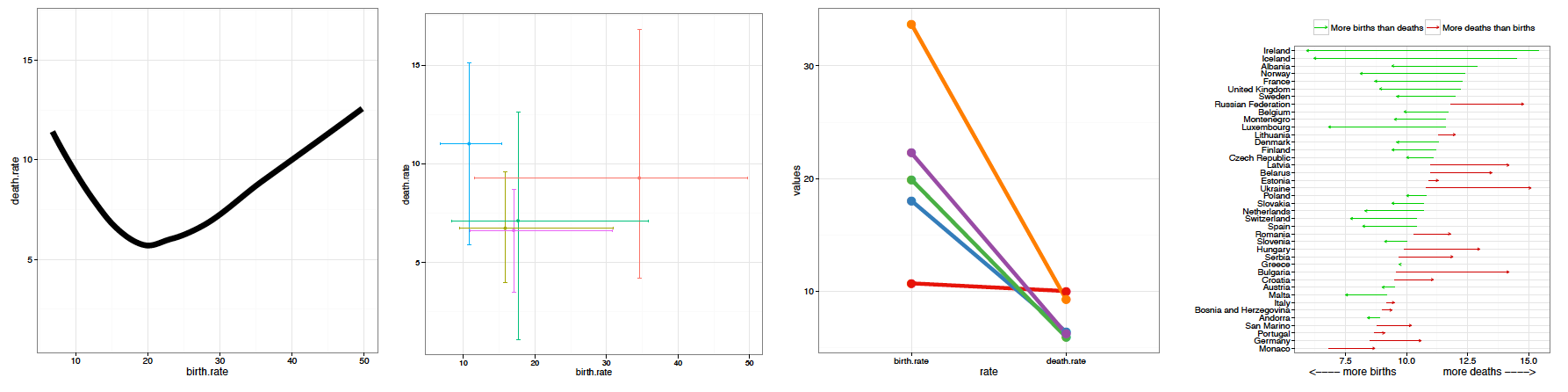 Rysunek 19: Prezentacja danych z użyciem linii. Możemy modyfikować również takie atrybuty jak typ linii, kolor czy wielkość
Rysunek 19: Prezentacja danych z użyciem linii. Możemy modyfikować również takie atrybuty jak typ linii, kolor czy wielkość
W pakiecie ggplot2 w wersji 2.0 dostępnych jest 27 różnych form. Dodatkowy mechanizm tworzenia nowych form pozwala na dodawanie własnych warstw o dowolnych kształtach i atrybutach. Liczba możliwości jest praktycznie nieograniczona, nie ma więc sensu omawianie wszystkich. Na rysunku 20 widnieje kilka wybranych.
Definicja formy jest otwarta, może to być dowolna kolekcja podobnych elementów graficznych, które nasze oko i mózg potrafią przypisać do jednej warstwy. Formą może być mozaika sześcioboków, a mogą być skrzypce, które szerokością kodują gęstość obserwacji, obszary krajów.
 Rysunek 20: Inne formy zastosowane do danych o demografii krajów. Pełna lista form jest dostępna na stronie http://docs.ggplot2.org
Rysunek 20: Inne formy zastosowane do danych o demografii krajów. Pełna lista form jest dostępna na stronie http://docs.ggplot2.org
Wiele geometrii wykorzystuje obszary, aby zakodować nimi dodatkową informację (np. skrzypce wyrażające gęstość). Proste obszary z estetycznymi kolorami potrafią podnieść atrakcyjność wykresu. Nie można ich jednak na wykresie umieścić zbyt wiele, przez co zazwyczaj stosuje się je do pokazania nie surowych obserwacji, ale statystyk z danych. Zobaczmy więc, jaką funkcję w GrGramatyce pełnią statystyki.
R odtwarzające przedstawione tutaj wykresy znajdują się na stronie http://bit.ly/1UkY53gStatystyki
Rysunek 21 przedstawia rozkład wyników matury z języka polskiego i matematyki w roku 2014. Z języka polskiego można było otrzymać od 0 do 75 punktów, więc za pomocą 76 słupków zaprezentowano liczbę osób, które uzyskały poszczególne wartości punktów. Maksymalny możliwy wynik z matematyki na poziomie podstawowym wynosił 50 punktów. Patrząc na ten wykres, łatwo jest określić, jakie wyniki uzyskiwali uczniowie oraz co dzieje się w pobliżu progu zaliczenia.
W świecie nazywanej grafiki taki wykres nazywa się histogramem i w wielu językach programowania można go zbudować funkcją hist() lub histogram()
Co jest szczególnego w tym wykresie z punktu widzenia GrGramatyki? Aby go zbudować, trzeba wykonać dwie operacje: (1) wyznaczyć liczebność osób, które uzyskały określone wyniki, (2) przedstawić te liczby za pomocą prostokątów zaczepionych na jednej wysokości. Innymi słowy: najpierw trzeba wyliczyć pewne statystyki z danych, a dopiero w następnym kroku przedstawić je graficznie.
GrGramatyka została tak zaprojektowana, by każdy niezależny element można było niezależnie opisywać i modyfikować. Celem jest ortogonalizacja poszczególnych składowych tworzenia wykresu. Rozdzielenie statystyki (tego, co ma być pokazane) i formy (jak ma być pokazane) zwiększa elastyczność i ułatwia logiczny rozkład wykresu.
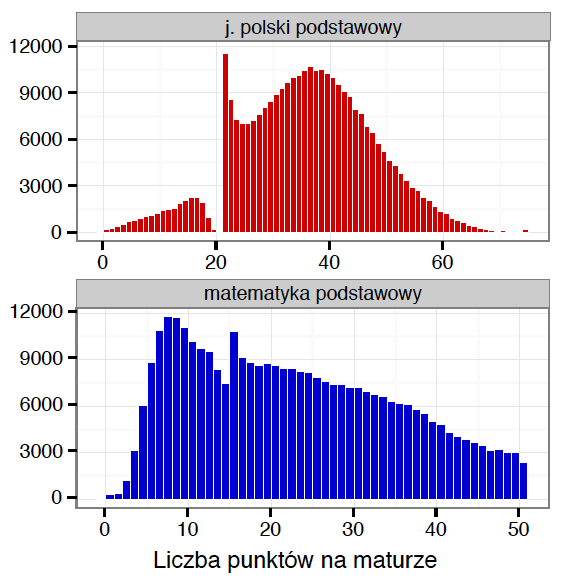 Rysunek 21:
Histogram z wynikami matur z języka polskiego i matematyki z roku 2014 na poziomie podstawowym. Zauważmy, że elementy wykresu nie przedstawiają poszczególnych obserwacji ze zbioru danych, ale agregaty/zliczenia
Rysunek 21:
Histogram z wynikami matur z języka polskiego i matematyki z roku 2014 na poziomie podstawowym. Zauważmy, że elementy wykresu nie przedstawiają poszczególnych obserwacji ze zbioru danych, ale agregaty/zliczenia
Wróćmy do danych o dynamice zmian populacji poszczególnych krajów. Na rysunku 22 przedstawiony został przykład statystyki dwuwymiarowej oceny gęstości, która w bibliotece ggplot2 jest wyznaczana funkcją stat_density_2d Zazwyczaj statystykę tę pokazuje się za pomocą konturów. W GrGramatyce możemy zmienić sposób prezentacji i przedstawić gęstości za pomocą wypełnionych poziomic, gradacyjnego przejścia kolorów czy też za pomocą wielkości kropek na siatce.
Ortogonalność w GrGramatyce uzyskuje się w ten sposób, że każda warstwa umożliwia niezależne wskazanie, jaka statystyka ma być wykorzystana do przetworzenia danych oraz jaka geometria posłuży do prezentacji statystyk. Rozgraniczając etap wyznaczania statystyk i etap rysowania danych, uzyskujemy elastyczność w składaniu form i statystyk.
Ktoś jednak może powiedzieć, że taką agregację danych można by wykonać wcześniej, przed tworzeniem wykresu. Po co więc GrGramatyka troszczy się o przetwarzanie, dlaczego nie pozostawić jej jedynie zadania rysowania danych?
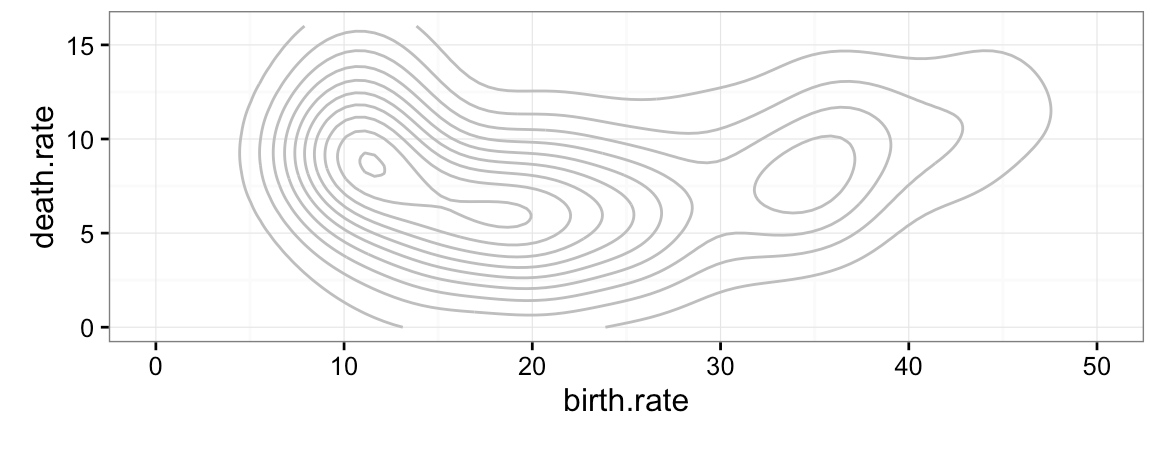
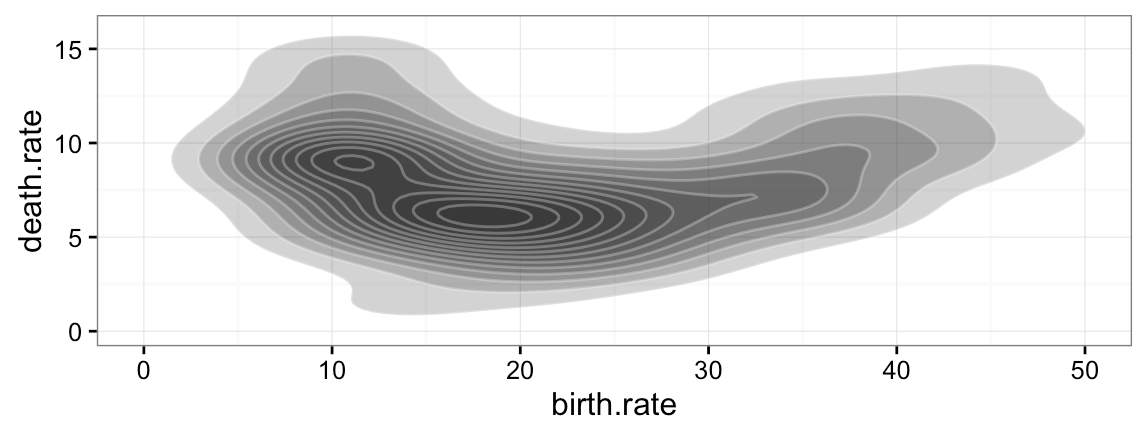
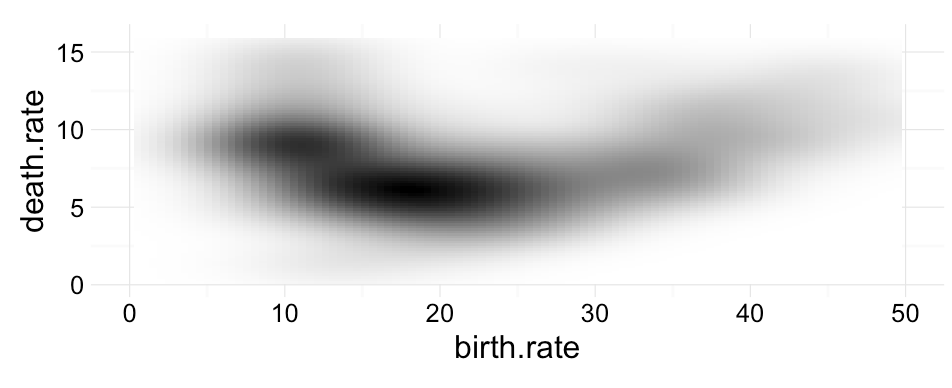
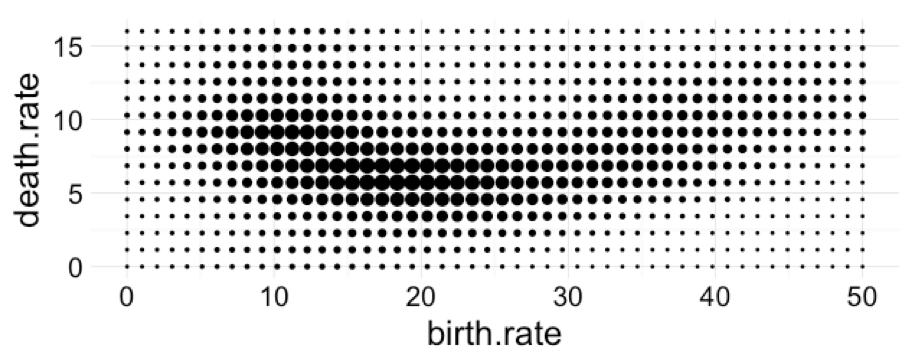 Rysunek 22: Statystyka dwuwymiarowej gęstości przedstawiona za pomocą różnych form
Rysunek 22: Statystyka dwuwymiarowej gęstości przedstawiona za pomocą różnych form
Odpowiedź na to pytanie wcale nie jest oczywista. Istnieją biblioteki, które wyraźnie rozdzielają agregowanie od rysowania. Umieszczenie etapu liczenia statystyk wewnątrz GrGramatyki ma jednak zalety. Widzimy źródłowy, oryginalny zbiór danych i łatwiej nam patrzeć na wykres jako na opis tego zbioru danych. Jeżeli wykres na różnych warstwach przedstawia różne statystyki wyznaczone na tym samym zbiorze danych, to łatwiej dostrzec wspólny szkielet.
Rysunek 23: Na tle kropek reprezentujących poszczególne kraje przedstawione są trzy kwartyle dzielące zbiór danych na cztery równoliczne części. Tę samą statystykę można pokazywać z użyciem różnych form
Przedstawmy to na przykładzie warstw opisujących trend. Wygodnie jest dodać do wykresu kilka alternatywnych krzywych trendu, aby zobaczyć, który lepiej pasuje do obserwacji. W GrGramatyce można zbudować wykres, składając kilka warstw – jedna warstwa z danymi surowymi i kolejne warstwy z krzywymi trendu. Przykład takiego złożenia jest przedstawiony na rysunku 24.
Poniżej znajduje się definicja tego wykresu.
ggplot(countries, aes(x = birth.rate, y = death.rate)) + geom_point(color="black") + geom_smooth(stat="smooth", method="lm", formula=y poly(x,1)) + geom_smooth(stat="smooth", method="lm", formula=y poly(x,2)) + geom_smooth(stat="smooth", method="loess", span=0.5)
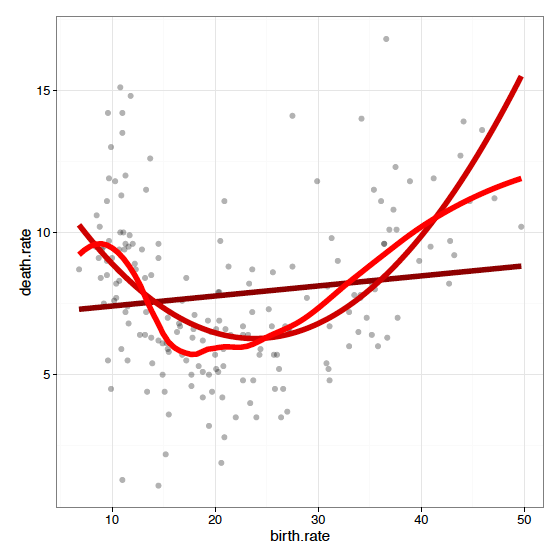 Rysunek 24: Na pierwszy rzut oka widać że trend liniowy jest bardzo złą aproksymacją danych, trend kwadratowy jest już znacznie lepszą. Nałożenie warstwy z surowymi danymi i różnymi trendami pozwala porównać wyniki pomiędzy sobą
Rysunek 24: Na pierwszy rzut oka widać że trend liniowy jest bardzo złą aproksymacją danych, trend kwadratowy jest już znacznie lepszą. Nałożenie warstwy z surowymi danymi i różnymi trendami pozwala porównać wyniki pomiędzy sobą
Każda warstwa w GrGramatyce jest opisana przez źródło danych oraz definicje statystyk, formy i modyfikatorów położenia. Zobaczmy, do czego służą modyfikatory.
R odtwarzające przedstawione tutaj wykresy znajdują się na stronie http://bit.ly/1RVv40gModyfikatory położenia
Każda warstwa wykresu składa się ze zbioru obiektów, których położenie jest określone przez zmienne zakodowane na atrybuty położenia. Może się zdarzyć, że kodowanie nie określa jednoznacznie położenia lub że obiekty kolidują ze sobą na wykresie. Dlatego GrGramatyka posiada dodatkowy mechanizm modyfikowania położenia elementów.
Na rysunku 25 przedstawiono na osi OX zmienną, która przyjmuje jedynie pięć różnych wartości. Z tego powodu kropki nachodzą na siebie w pionie, a w poziomie są między nimi duże odstępy. Stosując modyfikatory położenia, można zaradzić temu problemowi na różne sposoby. Pierwszym z nich jest dodanie zaburzenia losowego. Nie wprowadzamy systematycznego błędu, ale losowo “zaszumiamy” położenie, tak by kropki na siebie nie nachodziły. Druga możliwość to rozsuwanie kropek w bardziej usystematyzowany sposób, poprzez ułożenie nakładających się kropek na siebie.
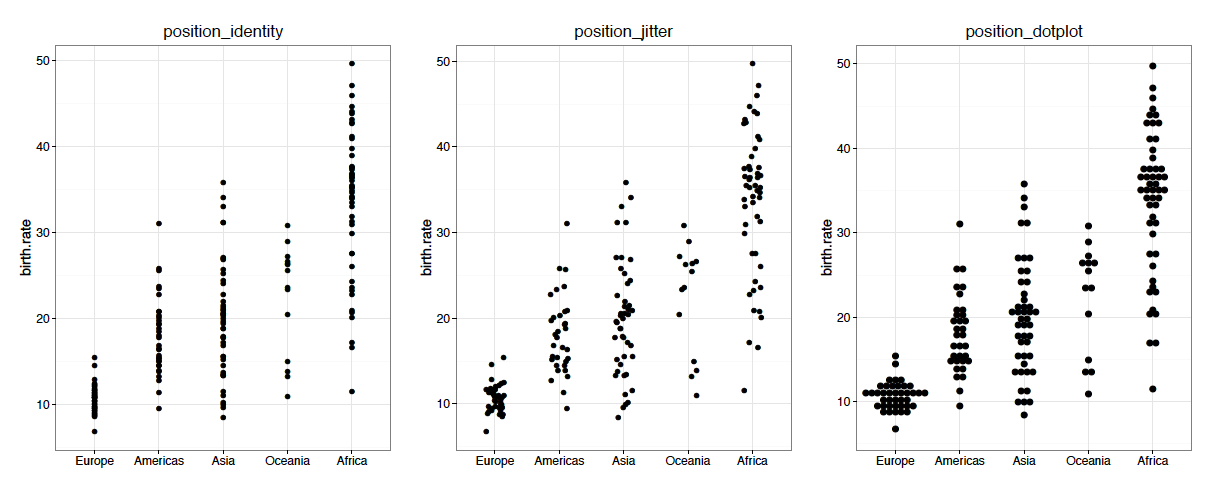
Rysunek 25: Warstwa z kropkami, w której kodowanie danych może spowodować, że kropkami nakładają się na siebie i są nieczytelne lub że warstwa wygląda mało atrakcyjnie. Poprzez modyfikację argumentu
position można kropki rozsunąć – albo dodając losowy szum, albo ustawiając je obok siebie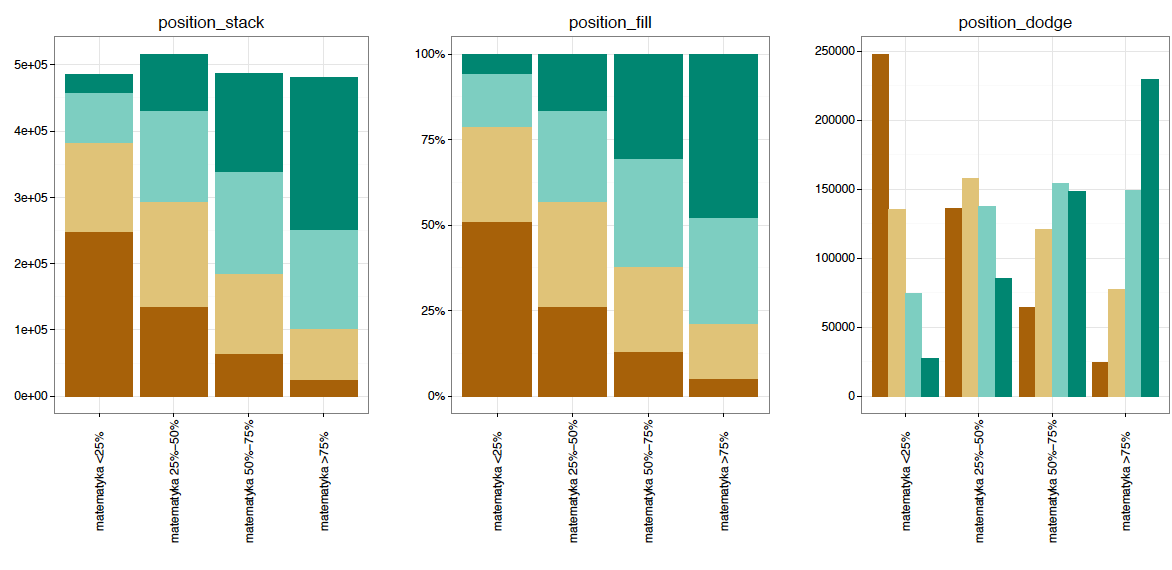
Podobne problemy mogą wystąpić, jeżeli składamy np. warstwy z kropkami i etykietami (etykiety trzeba przesunąć, aby było widać i etykiety, i kropki) lub gdy mamy warstwę z prostokątami o tych samych współrzędnych na jednej osi. Jeżeli do przedstawiania danych wykorzystujemy tylko długość prostokąta, to szerokość i położenie możemy dowolnie zmieniać, tak by prostokąty były czytelnie widoczne na wykresie. Można dookreślić, czy prostokąty o wspólnej współrzędnej powinny być obok siebie, czy na sobie. Poniżej definicja wykresu 25b.
ggplot(countries, aes(x = continent, y = birth.rate)) +
geom_point(position=position_jitter(width = 0.5, height = 0.5))
Rysunek 26: Warstwa z prostokątami określa położenie w poziomie i wysokość prostokątów. Nie dookreśla położenia w pionie. Trzy różne wartości argumentu
position dla tych samych danych powodują, że prostokąty są przedstawione na sobie, na sobie po unormowaniu lub obok siebieWszystkie warstwy umieszczone są w tych samych ramach określonych przez układ współrzędnych. Zobaczmy jaką funkcję w GrGramatyce pełni układ współrzędnych.
R odtwarzające przedstawione tutaj wykresy znajdują się na stronie http://bit.ly/1TuiAdQUkład współrzędnych
Jeden wykres ma jeden układ współrzędnych. Stanowi on ramy opowiadanej historii. W tych ramach rozmieszczone są elementy wykresu, można z nich odczytać zakresy zmiennych, oceniać bliskość obiektów lub odległość pomiędzy nimi. Aby odczytać jakąkolwiek informację z wykresu, musimy najpierw zidentyfikować i rozkodować układ współrzędnych.
Domyślnie dane prezentowane są w kartezjańskim układzie współrzędnych. Dwie prostopadłe, niezależne od siebie osie wypełniają cały dostępny obszar do rysowania. Jednak w określonych sytuacjach okazuje się, że dane możemy stosowniej przedstawić, jeżeli wykorzystamy inny układ współrzędnych.
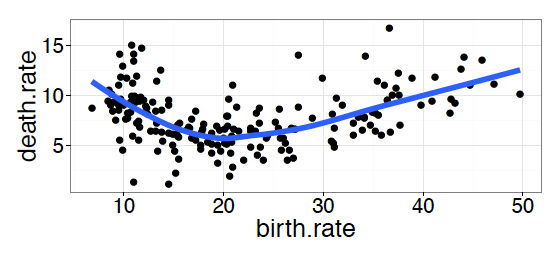 Rysunek 27: Układ z jednorodnymi osiami,
Rysunek 27: Układ z jednorodnymi osiami, coord_fixed
Przykładowo, jeżeli na obu osiach przedstawiamy zmienne wyrażone w tej samej jednostce, to dobrym pomysłem może być zachowanie proporcji na obu osiach. Pracujemy z danymi o urodzeniach i zgonach unormowanych na 1000 mieszkańców. W tym przypadku ma sens i może okazać się przydatne przedstawienie obu osi z zachowaniem proporcji. Dzięki temu jeden centymetr w poziomie będzie odpowiadał tej samej liczbie jednostek co jeden centymetr w pionie.
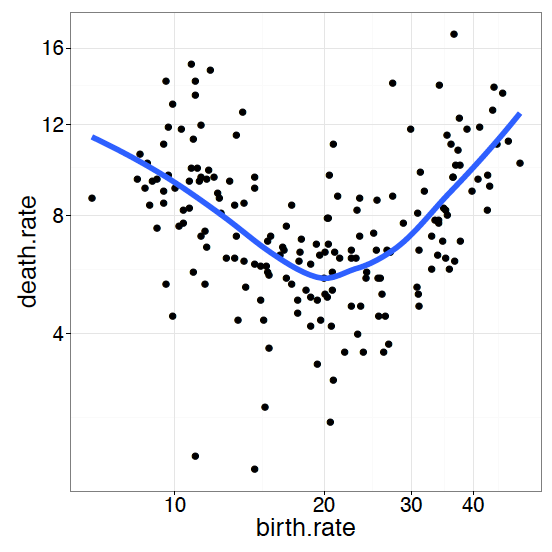 Rysunek 28: Układ współrzędnych z pierwiastkową transformacją osi
Rysunek 28: Układ współrzędnych z pierwiastkową transformacją osi
Być może dla naszej historii proporcje osi nie mają znaczenia, ale problemem może być skośność w danych. Może pokazujemy stężenia, które potrafią przyjmować wartości różniące się kilkoma rzędami wielkości, może przedstawiamy dane z pojedynczymi obserwacjami odstającymi od pozostałych wartości, a może prezentujemy prawdopodobieństwa, które są skupione w okolicy 0 lub 1. W takich przypadkach zastosowanie jednorodnych skali na osiach współrzędnych może spowodować, że większość obserwacji skupi się w jednym rogu wykresu, a pojedyncze obserwacje będą odległe od reszty. Aby lepiej wyeksponować interesujące zależności, często stosuje się transformacje zmiennych. Przykładowo w przypadku pokazywania stężeń niejednokrotnie wykorzystuje się transformację logarytmiczną. Jeżeli dane zawierają wartości zerowe, to stosuje się transformację pierwiastkową lub logarytm 1 + x. Prezentacja prawdopodobieństw często wykorzystuje transformację logistyczną lub probitową.
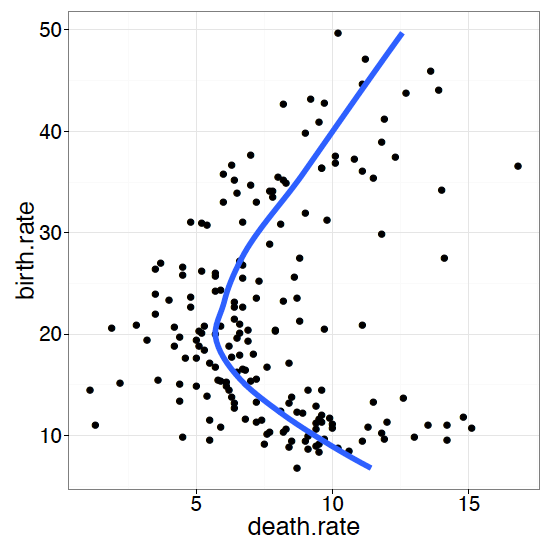 Rysunek 29: Układ z odwróconymi osiami
Rysunek 29: Układ z odwróconymi osiami
Zmiany układu współrzędnych mogą dotyczyć np. zamiany osi. Od szkoły podstawowej uczymy się, że zależności funkcyjne mają argumenty na osi poziomej, a wartości na osi pionowej. Dlatego gdy przedstawiamy zależności typu trend, rozkład w grupach (tzw. wykresy pudełkowe), to argumenty są najczęściej na osi poziomej. Jednak niekiedy dobrym pomysłem może być zamiana/odwrócenie osi.
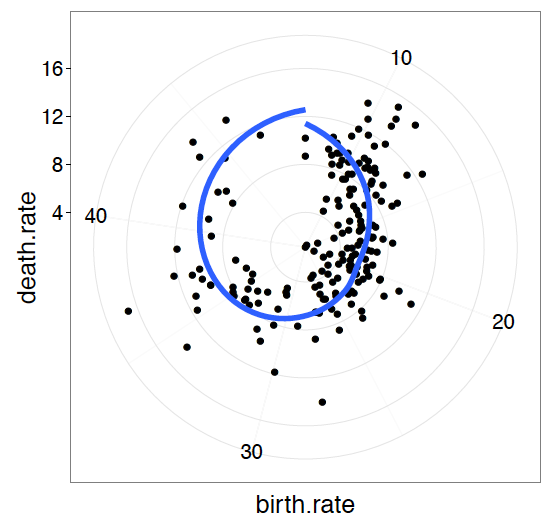 Rysunek 30: Biegunowy układ współrzędnych
Rysunek 30: Biegunowy układ współrzędnych
Jeszcze inny przykład zmiany osi polega na zastąpieniu układu kartezjańskiego układem biegunowym. Po co? Może to być dobry pomysł, gdy przedstawiamy zmienne z okresowymi wartościami, np. daty (okres to tydzień, miesiąc lub rok), i chcemy zaznaczyć periodyczność wartości na skali. Inna taka sytuacja, to gdy prezentowana zmienna w naturalny sposób powinna być odwzorowywana na okręgu (np. kąty).
Dobór układu współrzędnych odgrywa szczególnie ważną rolę w przypadku, gdy przedstawiamy dane geograficzne. Ziemia jest w przybliżeniu sferą i nie da się jej idealnie odwzorować na płaszczyźnie. Rolę układu współrzędnych przyjmuje tu odwzorowanie geograficzne. Różne odwzorowania mogą okazać się dobre, w zależności od tego, czy chcemy dokładnie przedstawić kąty, pola czy odległości. Przykładowo odwzorowanie walcowe Merkatora zachowuje kąty pomiędzy południkami i równoleżnikami (patrz rysunek 31), odwzorowanie Mollweidego zachowuje powierzchnię (patrz rysunek 32), odwzorowanie Postela stara się zachować odległości. W zależności od tego, czego dotyczy prezentowana historia, należy wybrać odpowiednie odwzorowanie.
Z uwagi na konsekwencje odwzorowania geograficzne powinniśmy wybierać uważnie. Popularność odwzorowania Merkatora na szkolnych mapach pozostawiła u wielu osób wrażenie, że Europa ma wielkość porównywalną do Afryki. Odwzorowanie Merkatora powiększa obszary blisko biegunów, a zmniejsza w okolicy równika. Powoduje to, że nie widać na nim, że powierzchnia Afryki jest trzykrotnie większa niż Europy. Poniżej zaprezentowano definicję wykresu 32.
ggplot() + geom_map(data=countries, map=map.world,
aes(map_id=region, x=long, y=lat, fill=birth.rate)) +
coord_map("mollweide")
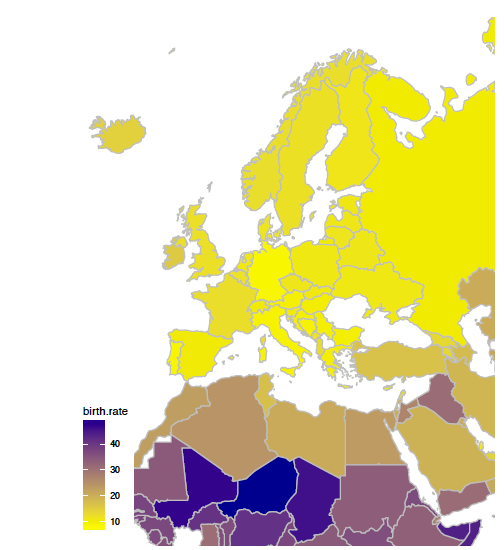 Rysunek 31: Odwzorowanie Gerarda Merkatora zachowuje kąty
Rysunek 31: Odwzorowanie Gerarda Merkatora zachowuje kąty
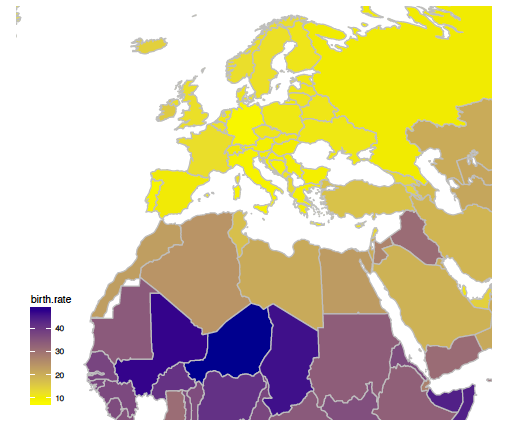 Rysunek 32: Odwzorowanie Carla Mollweidego, zachowuje powierzchnie
Rysunek 32: Odwzorowanie Carla Mollweidego, zachowuje powierzchnie
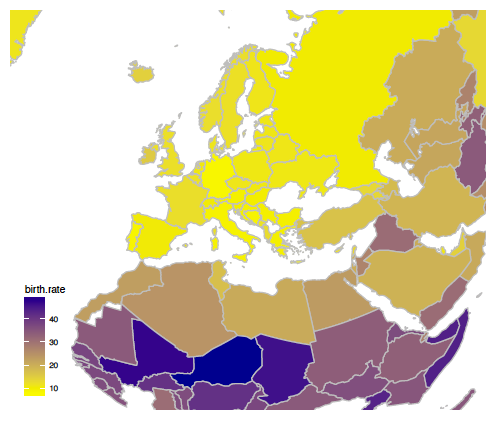 Rysunek 33: Rzut prostokątny kuli ziemskiej
Rysunek 33: Rzut prostokątny kuli ziemskiej
Wybór układu współrzędnych nie jest jedynym sposobem transformowania zmiennych. Innym jest modyfikacja skali.
R odtwarzające przedstawione tutaj wykresy znajdują się na stronie http://bit.ly/22CP0ciPodziałki/skale
Układ współrzędnych stanowi ramy, w których toczy się historia. Historie są budowane przez kolejne warstwy. Na warstwach dane są zakodowane za pomocą atrybutów graficznych. Sposób kodowania zmiennych określają skale. Skale są wybierane w zależności od typu danych i rodzaju atrybutu. Inna skala będzie dobra dla zmiennych ilościowych, inna dla jakościowych.
Zazwyczaj skale są tworzone automatycznie, ale istnieją sytuacje, w których chcemy wyłączyć autopilota i wziąć w swoje ręce kontrolę sposobu, w jaki dane są przekształcane. GrGramatyka umożliwia określenie kodowania każdego graficznego atrybutu. Skale są definiowane globalnie dla całego wykresu i są stosowane do wszystkich warstw jednolicie.
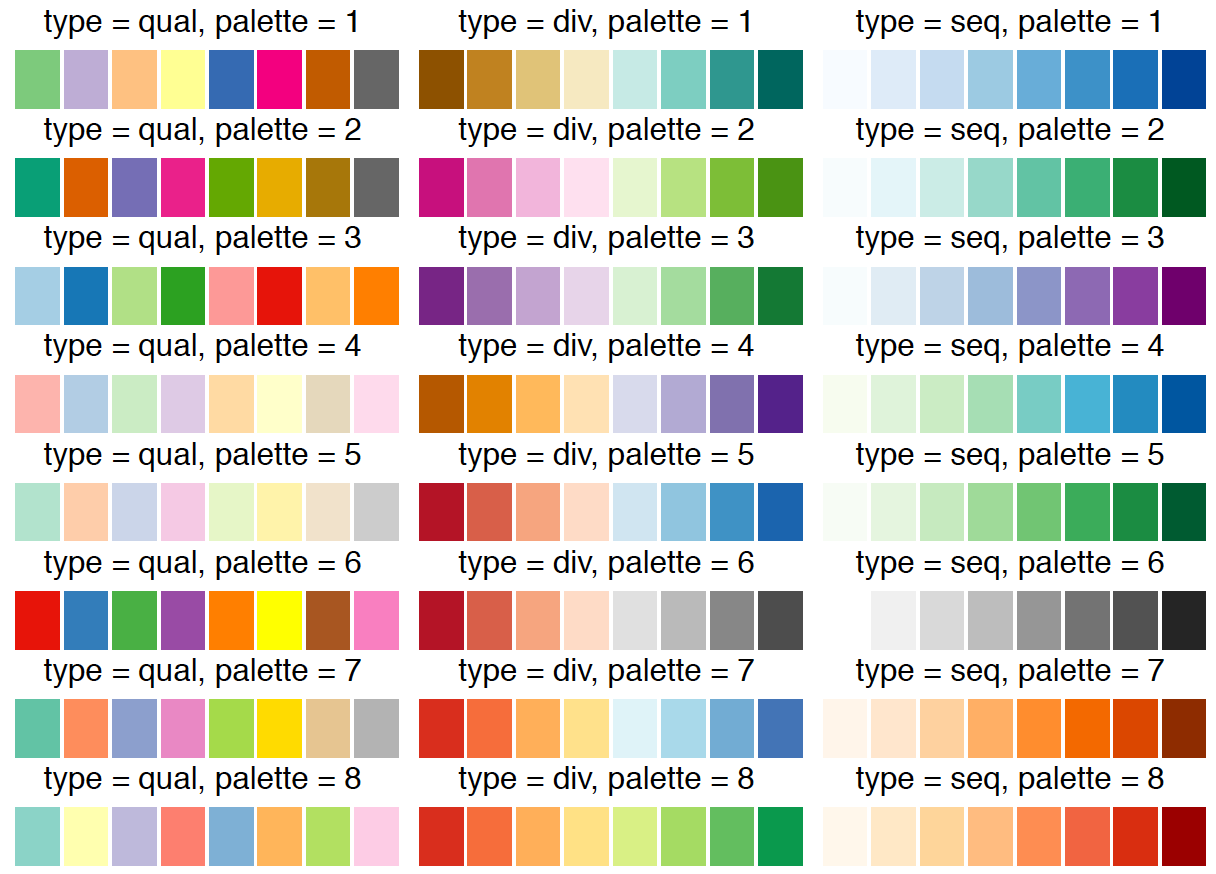
Jedną z najczęściej zmienianych skal jest skala kolorów. Zmieniana jest nie dlatego, że domyślne kolory są złe, ale często dlatego, że wiele osób ma własne preferencje w tym zakresie i są one zazwyczaj bardzo różne lub z uwagi na spójność z barwami firmowymi.
O doborze kolorów pisałem szeroko w eseju “Percepcja kolorów”. Określając mapowanie zmiennej na kolor wypełnienia czy kolor brzegu, należy wskazać, czy zmienna jest w skali uporządkowanej, czy jakościowej, czy ma element neutralny, czy nie. Ustaliwszy to, mamy zazwyczaj do wyboru kilka palet kolorystycznych, które w sposób ciągły rozpinają się pomiędzy dwoma lub trzema kolorami (zobacz rysunek 34).
Rysunek 34: Definiując skale dla koloru, musimy określić dwie rzeczy. Po pierwsze, ile różnych wartości mamy do zakodowania. Po drugie, z jakiego rodzaju zmienną pracujemy: czy jest to zmienna w skali uporządkowanej, w skali z elementem neutralnym, czy w skali jakościowej. Na rysunku widnieją kolory zaproponowane przez Cynthię Brewer do przedstawienia ośmiu kolorów dla zmiennych jakościowych (pierwsza kolumna) oraz ilościowych z elementem neutralnym lub bez (kolejne dwie kolumny). Wiersze pokazują osiem różnych możliwych skali dla każdego z wybranych układów
Innym bardzo interesującym atrybutem oprócz koloru jest kształt. Z jednej strony umożliwia on precyzyjne przedstawienie danych, z drugiej – nie ma oczywistych metod kodowania liczb na kształty symboli. Podstawowe problemy z kształtami, podobnie jak z kolorami, dotyczą kwestii zapewnienia ich rozróżnialności. Jeżeli wybierzemy zbyt dużo różnych symboli, to czy ktoś rozróżni małe otwarte koło od dużego otwartego koła? Czy dwa przecinające się trójkąty nie wytworzą trzeciego trójkąta, przez co trudno określić, co jest osobną kropką a co tylko przecięciem dwóch większych kropek?
Nie ma jednej uniwersalnej skali wyboru kształtu kropek. Rysunek 35 prezentuje kształty domyślnie stosowane w różnych pakietach statystycznych. Gdy trzeba przedstawić wiele różnych symboli, często wykorzystywane są duże litery. Ale nie jest to idealne rozwiązanie. Czy w chmarze literek C i G rozróżnimy jedne od drugich? A U i V czy też E i F? Ich kształty są na tyle podobne, że łatwo pomylić jedne z drugimi.
Dlatego też kształt, podobnie jak kolor, najlepiej się sprawdza, jeżeli do przedstawienia jest jedynie kilka różnych wartości. Lub gdy kropki, które prezentujemy, nie ma zbyt wiele. Ciekawą dyskusję o wadach i zaletach różnych kształtów umieszczono w artykule Points of view: Plotting symbols.
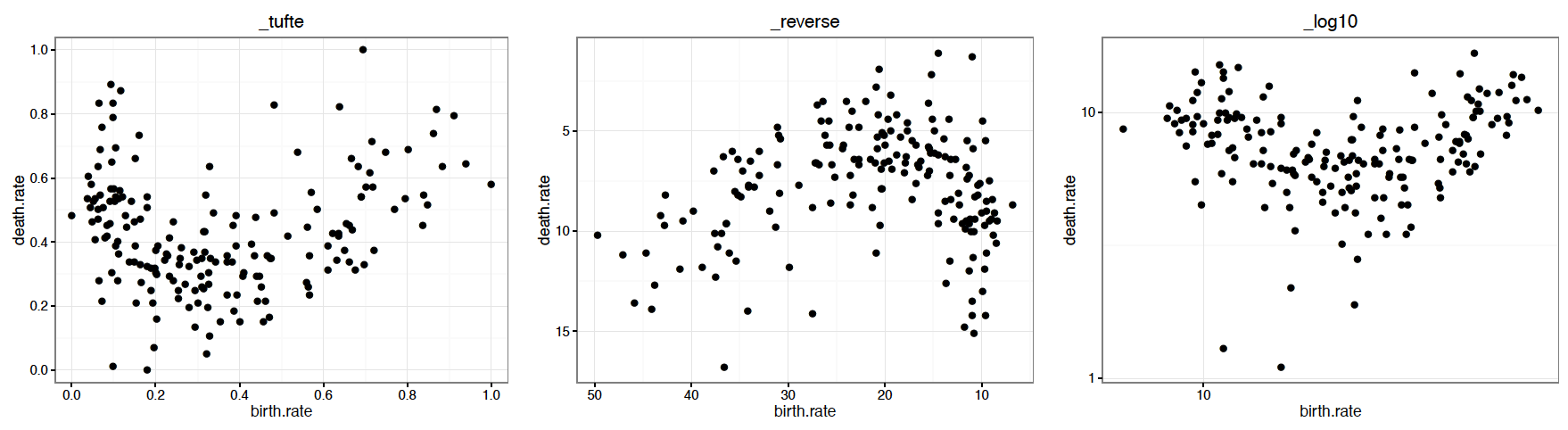
Skale można definiować dla każdego atrybutu, w tym na przykład wielkości (możemy określić, jak duży symbol ma odpowiadać danej wartości kodowanej zmiennej) czy położenia. W finansach i genetyce często mamy do czynienia ze zmiennymi silnie skośnymi, to znaczy takimi, w których pojedyncze obserwacje mogą być kilka rzędów wielkości większe od większości pozostałych. Pozostawienie liniowej skali w tym wypadku doprowadziłoby do tego, że większość obserwacji znajdowałaby się bardzo blisko siebie, a tylko pojedyncze odstawałyby od reszty. Zamiast więc liniowej skali do zaprezentowania tych zmiennych przyjmuje się zazwyczaj inną, np. logarytmiczną. Jeżeli z jakiegoś powodu logarytm jest złym rozwiązaniem, można wybrać pierwiastek lub dowolną inną monotoniczną funkcję. Na rysunku 36 przedstawiono te same dane dla różnych transformacji skali.
Warto zauważyć, że poprzedni punkt dotyczył transformacji osi układu współrzędnych. Czym one się różnią od transformacji skali? Różnica polega na działaniu statystyk. Transformacje skali są przeprowadzane przed zastosowaniem statystyk, a transformacje układu współrzędnych – po. A więc jeżeli dopasowujemy do danych trend liniowy i zastosujemy transformację logarytmiczną skali, to otrzymamy trend liniowy dla zlogarytmowanych zmiennych. Ale jeżeli użyjemy transformacji układu współrzędnych, to uzyskamy trend liniowy dla oryginalnych zmiennych pokazany na wykresie o przekształconych osiach. Taki trend w przekształconym układzie współrzędnych nie będzie już linią prostą.
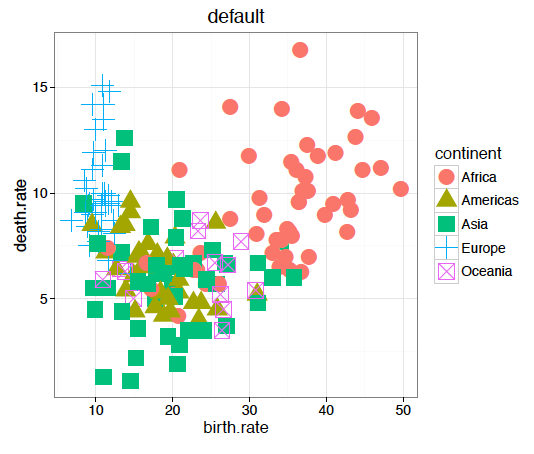
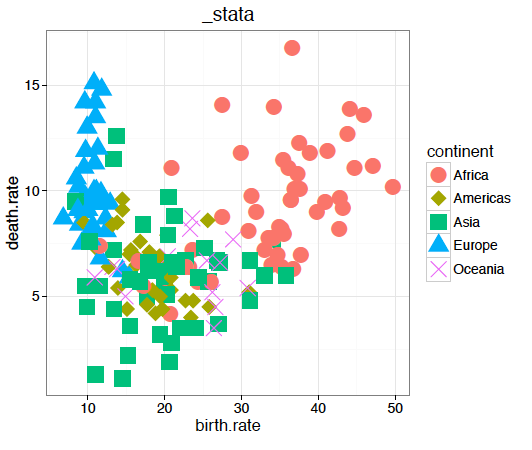
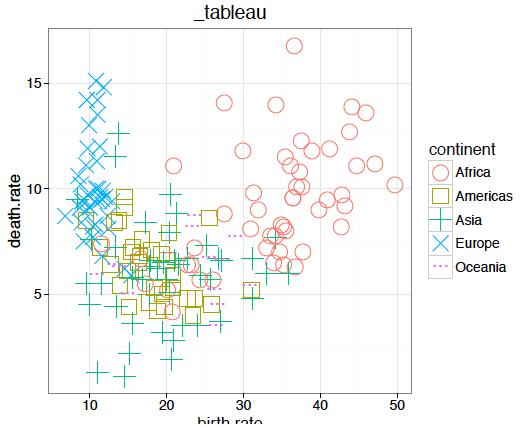
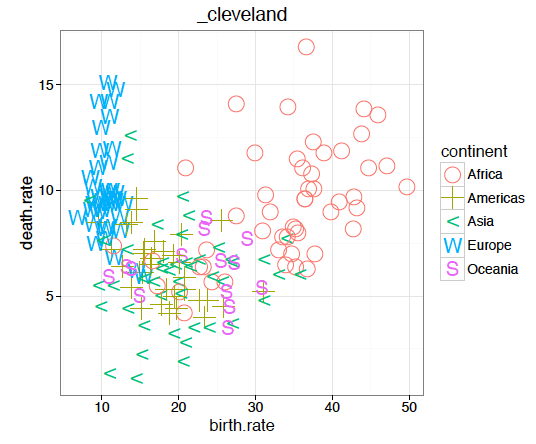
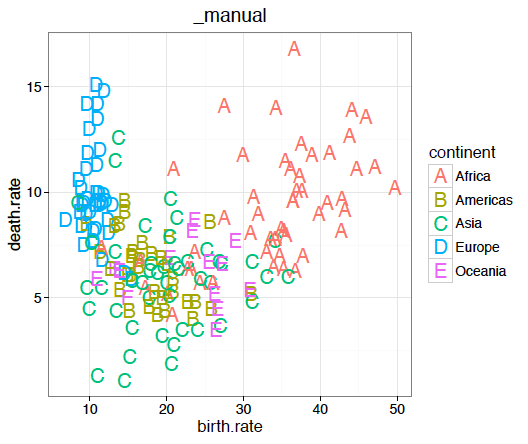 Rysunek 35:
Nie istnieje uniwersalny zbiór symboli wykorzystywanych do kodowania zmiennych jakościowych. Kolejne wykresy pokazują propozycje z popularnych pakietów graficznych i arkuszy kalkulacyjnych
Rysunek 35:
Nie istnieje uniwersalny zbiór symboli wykorzystywanych do kodowania zmiennych jakościowych. Kolejne wykresy pokazują propozycje z popularnych pakietów graficznych i arkuszy kalkulacyjnych
Poniższa definicja wykresu określa skale dla koloru (od żółtego do ciemnoniebieskiego) oraz dla kształtów (litery).
ggplot(countries, aes(x=birth.rate, y=death.rate, color=continent, shape=continent)) + geom_point() + scale_color_gradient(low = "yellow", high = "blue4") + scale_shape_manual(values=LETTERS)
R odtwarzające przedstawione tutaj wykresy znajdują się na stronie http://bit.ly/1PBT0lXPanele/oblicza
Edward Tufte spopularyzował metodę small multiples, która przedstawia różne oblicza podzbiorów danych za pomocą serii wykresów osadzonych w tych samych ramach, w tym samym układzie współrzędnych. Znacznie łatwiej porównać obserwacje na różnych wykresach, jeżeli są one osadzone w tych samych ramach.
GrGramatyka pozwala na wskazanie jednej lub większej liczby zmiennych grupujących do przedstawienia różnego oblicza danych. Przy zastosowaniu tego mechanizmu każda grupa obserwacji jest prezentowana na osobnym panelu.
Takie rozbicie danych na serię paneli ułatwia porównanie dużej liczby grup. Gdyby je bowiem wszystkie zestawić na jednym wykresie, to nałożone na siebie uczynią cały wykres mało czytelnym. Przykład z pięcioma grupami jest przedstawiony na wykresach 38 i 37. Poniżej znajduje się ich definicja.
ggplot(countries, aes(x = birth.rate, y = death.rate)) + stat_ellipse(color="red4") + geom_point(size=2, color="red") + facet_wrap( continent)
 Rysunek 37: Dane jak na Rysunku 28 ale wszystkie grupy na jednym panelu}
Rysunek 37: Dane jak na Rysunku 28 ale wszystkie grupy na jednym panelu}
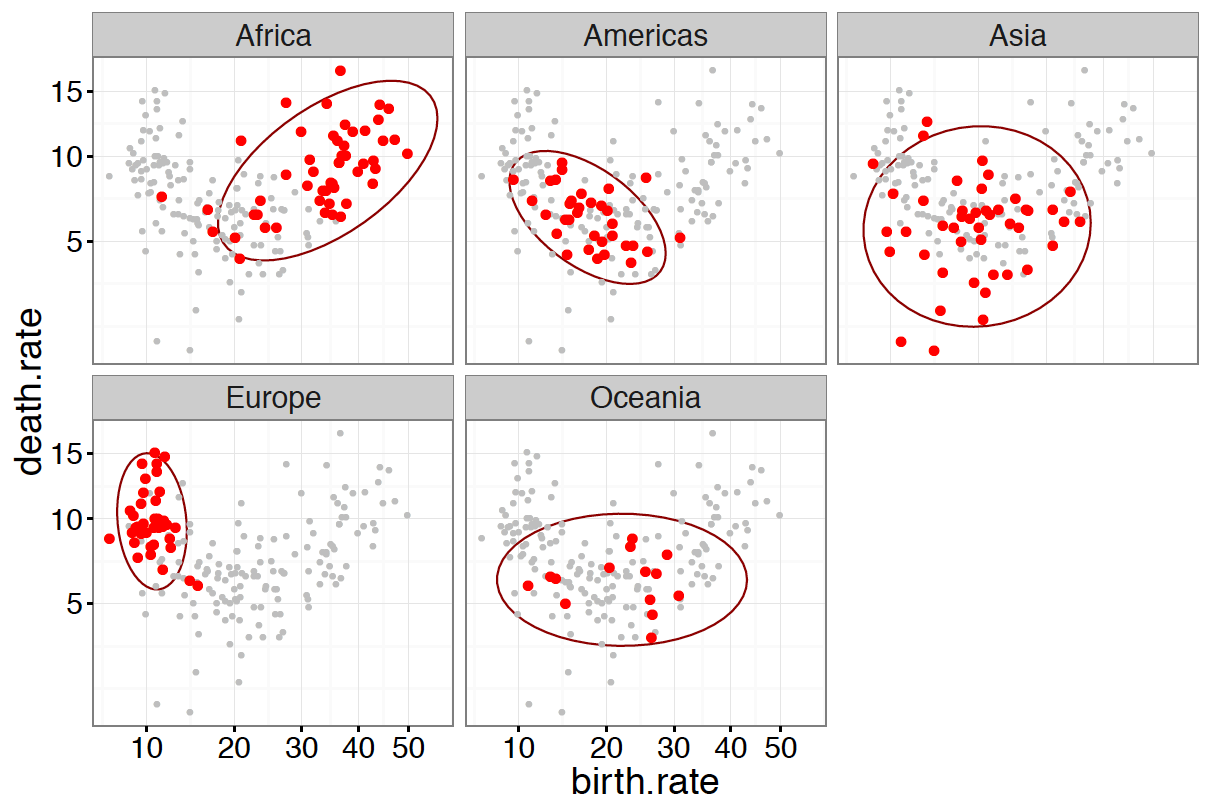
Rysunek 38: Wykres przedstawia częstości zgonów i narodzin dla poszczególnych kontynentów na osobnych panelach
Motywy graficzne/skórki
Na wykresie poza elementami przedstawiającymi dane występują też bardzo ważne elementy niezwiązane z danymi. Przykładowo: tło wykresu, krój tytułu wykresu czy wielkość etykiet na osiach. Takie składniki silnie wpływają na wygląd wykresu, zatem ich opis również powinien się znaleźć w GrGramatyce. Szukając analogii do języka, moglibyśmy je porównać do intonacji, akcentu czy dykcji. Są one niezależne od wypowiadanej treści, ale mogą ją wzmocnić lub osłabić.
Rysunek 39 przedstawia ten sam wykres z nałożeniem rozmaitych skórek. Jak widzimy, geometria danych się nie zmienia, ale wykres wygląda zupełnie inaczej. GrGramatyka umożliwia dookreślenie każdego elementu graficznego osobno, pozwala też na tworzenie tzw. skórek, a więc zbiorów parametrów graficznych, które mogą być dodane do każdego wykresu – tak jak na poniższym przykładzie.
ggplot(countries, aes(x = birth.rate, y = death.rate)) + geom_point() + theme_economist()
Ściągawka
W tym eseju opisałem GrGramatykę kładąc nacisk na strukturę i znacznie elementów wykresu. Gdzie nie gdzie pojawiały się instrukcje w programie R, ale wyłącznie w celu ilustracji. Dla osób, które chciałyby poznać pełną listę skal, geometrii, statystyk na kolejnej stronie umieściłem ściągawkę wykonaną przez firmę RStudio i udostępnioną na licencji Creative Commons. Zawiera ona listę najważniejszych funkcji z pakietu ggplot2
Reprodukowalność
Kolejną ważną kwestią jest odtwarzalność procesu tworzenia wykresów. Wykresy w GrGramatyce są opisane przez sekwencje wywołań funkcji programu R Wykresy nie są “wyklikane” w jednym czy drugim narzędziu. Uzyskujemy zapis wykresu, który można w każdej chwili odtworzyć lub zmodyfikować.
Wszystkie wykresy zaprezentowane w tym eseju zostały wykonane w GrGramatyce z użyciem pakietu ggplot2 Definicje w programie R oraz miniatury przedstawionych wykresów znajdują się na stronie http://bit.ly/1R54Zw6 Każdy wykres przedstawiony w tym rozdziale można odtworzyć i powiększyć za pomocą przedstawionego na tej stronie kodu.
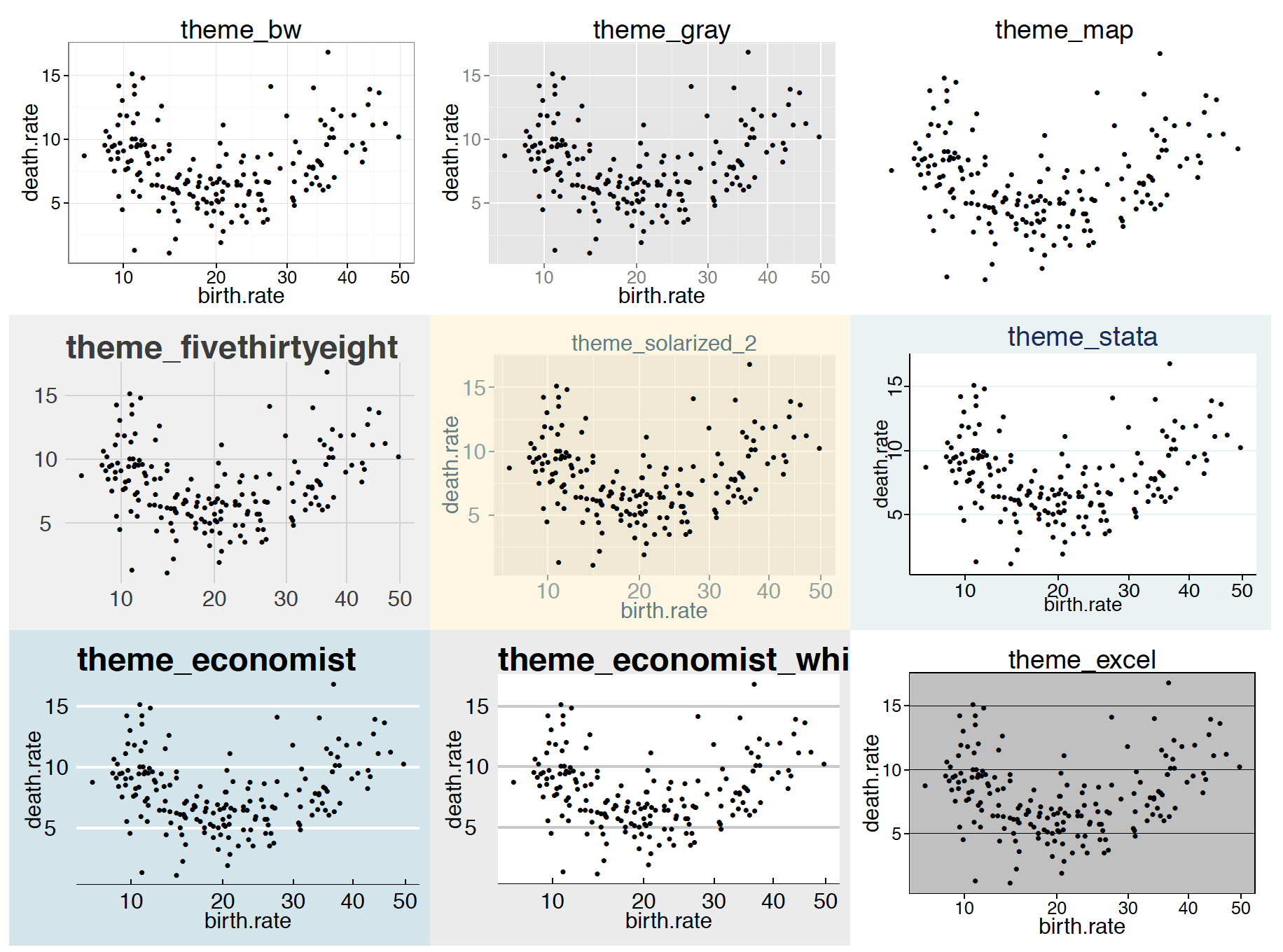 Rysunek 39: GrGramatyka pozwala na kontrolę nad każdym detalem na wykresie. Na kolejnych panelach przedstawiony jest ten sam wykres z zastosowaniem różnych skórek/motywów. Nazwa skórki umieszczona jest w tytule wykresu
Rysunek 39: GrGramatyka pozwala na kontrolę nad każdym detalem na wykresie. Na kolejnych panelach przedstawiony jest ten sam wykres z zastosowaniem różnych skórek/motywów. Nazwa skórki umieszczona jest w tytule wykresu
Odtwarzalność wyników, a więc także wykresów, jest fundamentem publikacji naukowych, ale też każdego porządnego raportu. Jeżeli w raporcie lub publikacji widzimy wykres z interesującymi zależnościami, czyż nie jest naturalne oczekiwać, że dany wykres można odtworzyć? GrGramatyka pozwala na taką odtwarzalność. Oferuje jeden spójny język łączący zmienne oraz zależności w danych z graficznymi atrybutami elementów przedstawionych na wykresie.
