Osoby zajmujące się analizą danych wiedzą, jak ważną rolę pełni graficzna prezentacja danych i wyników analiz. Jest ona istotna zarówno na wczesnym etapie poznawania i rozumienia zależności opisywanych przez dane, jak i na późnym etapie prezentacji tych zależności innym osobom. Jest tak w środowisku naukowym (grafiki w czołowych czasopismach naukowych są czasem przygotowywane przez zawodowych projektantów), w mediach przy wiadomościach opartych o dane, w biznesie i w przemyśle. Czytelna i komunikatywna wizualizacja danych wzmacnia siłę wyników, a nieprzemyślana lub nieczytelna podważa rzetelność przeprowadzonych analiz.
O ile jednak coraz więcej osób dostrzega wartość dodaną dobrego graficznego przedstawienia danych, to wciąż niewiele osób uświadamia sobie skąd ta wartość się bierze, błędnie zakładając, że składa się na nią wyłącznie estetyka prezentacji
W tym eseju będziemy zamiennie używać pojęć: grafika statystyczna, infografika, graficzna prezentacja danych czy wizualizacja danych, mając świadomość, że każde z nich może oznaczać coś innego dla różnych osób. Zamiast jednak zaczynać od precyzyjnej definicji tego czym jest wizualizacja danych, wolę zmierzyć się z pytaniem co jest wyróżnikiem dobrej graficznej prezentacji danych?
Gdzie znaleźć odpowiedzi na to pytanie? Ja poszukam ich w historii wizualizacji danych. Wybrałem grupę moim zdaniem najciekawszych przykładów, które opiszę w formie krótkich podrozdziałów. Przykłady uporządkowałem chronologicznie, traktując je jako osobne i jednocześnie bardzo istotne przystanki w podróży przez dzieje wizualizacji danych. Zatrzymujemy się na dłużej tam, gdzie twórcy tej sztuki dokonali prawdziwych przełomów
Steve Jobs
Moim zdaniem dobra wizualizacja to taka, która dużo pokazuje już przy pierwszym spojrzeniu, ale ma również wiele do zaoferowania dla osób chcących ją dłużej studiować. Pozostawia miejsce na dalsze odkrycia w miarę stopniowego jej poznawania oraz łączenia jej składowych w spójną i ciekawą historię. Jest jak zagadka, która rozwiązującemu oferuje momenty: Acha! A więc tak to jest! To ciekawe! Zdarza się, że dobra wizualizacja jest wielowątkową lub szkatułkową opowieścią, w której pierwsze odkrycia odczytane z wykresu są wprowadzeniem do kolejnych.
Proszę potraktować poniższe podrozdziały jako zaproszenie do odkrywania piękna i bogactwa wizualizacji danych, które przemawia nie tylko poprzez estetykę prezentacji, ale przede wszystkim przez wartość przedstawianej informacji. Liczę, że poniższe przykłady wielkich wizualizacji stworzą ramy dla odpowiedzi na pytanie, czym jest dobra prezentacja danych. Ramy te będziemy wypełniać na dalszych stronach tej książki.
Alexis de Tocqueville
Wizualizacja danych to opowiadanie historii
Dlaczego warto przedstawiać dane graficznie? Jednym z argumentów może być to, że jako gatunek mamy najlepiej rozwinięty zmysł wzroku, który odgrywał i nadal odgrywa olbrzymią rolę w codziennym funkcjonowaniu. Właśnie ten zmysł pozwalał nam znaleźć jadalne jagody czy wypatrzeć jakiegoś drapieżnika. Można powiedzieć, że taki sposób zdobywania informacji o otaczającym nas świecie “siedzi” w człowieku od zarania dziejów. Zanim jeszcze wynaleziono pismo, zanim wynaleziono cyfry, kilkanaście tysiącleci przed naszą erą ludzkość nauczyła się przekazywać historię za pomocą malowideł naskalnych.
Historie łowieckie, obrazy pradawnych zwierząt, opisy rytuałów – to wszystko było tematem malunków na ścianach jaskiń. Dlaczego pierwotny człowiek, zamiast poprzestać na przekazie słownym, skrobał na ścianie wizerunek polowania?
Być może już tysiące lat temu zauważono, że przy opowiadaniu historii odpowiednie jej zilustrowanie pozwala lepiej tę historię zrozumieć. I choć naskalne malunki nie przypominają w niczym dzisiejszych wykresów, łączy je z nimi silna więź. Tak współczesne wykresy, jak i malunki sprzed 17 tysięcy lat służą czytelnemu przedstawieniu pewnej historii, opowieści lub zjawiska. Można je wykorzystać, aby wzmocnić ustną narrację albo pozostawić do samodzielnej kontemplacji.
 Rysunek 1: Malowidło naskalne z jaskini Chauveta, Francja. Źródło: Wikipedia, domena publiczna
Rysunek 1: Malowidło naskalne z jaskini Chauveta, Francja. Źródło: Wikipedia, domena publiczna
W artykułach naukowych, w codziennej prasie, w przemówieniach i tekstach popularnonaukowych posługujemy się językiem pisanym. Dlaczego? Ponieważ pisania i czytania uczymy się już w pierwszej klasie szkoły podstawowej, traktujemy pismo jako podstawowy środek komunikacji zaraz po języku mówionym, który poznajemy jako dzieci jeszcze wcześniej.
Słowo pisane to medium, które większość z nas opanowała w wysokim stopniu. Daje ono dużą precyzję i pozwala na wyrażenie bardzo dużej gamy komunikatów. Pomimo precyzji, którą ono daje, specjaliści od komunikacji zauważyli, że artykuły w gazetach, blogi, przemówienia przyciągają więcej czytelników i bardziej zapadają w pamięć, jeżeli są “ozdobione” schematem, wykresem lub inną grafiką ilustrującą całą wypowiedź. Dobrze przygotowany rysunek daje natychmiastowy obraz tego, jak wygląda główny nurt opisywanej historii, jaki jest jej szkielet. Mając ten obraz, znacznie łatwiej jest zanurzyć się w tekst – zarówno w żmudne szczegóły, jak i w szerokie wyjaśnienia.
 Rysunek 2: Malowidło naskalne z jaskini Lascaux, Francja. Źródło: Wikipedia, domena publiczna
Rysunek 2: Malowidło naskalne z jaskini Lascaux, Francja. Źródło: Wikipedia, domena publiczna
Świadczy to o potędze możliwości, jaką kryje w sobie graficzne przedstawienie historii opartej na danych. Nawet jeżeli historia jest szczegółowo przedstawiona za pomocą tekstu, nawet jeżeli planujemy przez godzinę barwnie ją opisywać, to w każdym z tych przypadków zwiększymy skuteczność przekazu, jeżeli dostarczymy skrótu w postaci wykresu czy schematu bezpośrednio do systemu wizualnego mózgu odbiorcy.
 Rysunek 3: Malowidło naskalne z jaskini Lascaux, Francja. Źródło: Wikipedia, domena publiczna
Rysunek 3: Malowidło naskalne z jaskini Lascaux, Francja. Źródło: Wikipedia, domena publiczna
Co to za hieroglify?
Przenieśmy się teraz w trochę mniej odległą przeszłość, w okres ostatnich trzech tysiącleci przed naszą erą. W tym czasie w Egipcie stosowano pismo hieroglificzne, oparte na hieroglifach, czyli – zgodnie z językiem starogreckim – “świętych znakach”.
Co wspólnego mają hieroglify z prezentowaniem danych? Przypuszczam, że wielu mogłoby stwierdzić, że dla nich wykresy statystyczne są równie czytelne co egipskie hieroglify. Użyliby tego porównania dla podkreślenia, że oba te twory są dla nich kompletnie niezrozumiałe.
Jest tak dlatego, że zarówno wykresy statystyczne, jak i egipskie hieroglify bazują na abstrakcji i używają symboli, których znaczenie zmienia się w zależności od kontekstu. Odbiorca musi znać kod przekładający symbole i kombinacje symboli na ich niedosłowne znaczenie, aby odczytać znaczenie hieroglifów. Wbrew potocznemu przekonaniu hieroglify to nie seria obrazków, które obrazują pewną historię, jak to miało miejsce w przypadku malowideł naskalnych. Przykładowo seria symboli: knot, krzesło, chleb i ptak, nie oznacza, że przy palącej się świecy stało krzesło, a na nim był chleb, który następnie porwał ptak. Symbole mają określone niedosłowne znaczenie. Na przykład symbol “knot” (pierwszy po lewej na rysunku na marginesie) oznacza spółgłoskę “h”.
Przyjrzyjmy się bliżej gramatyce hieroglifów. Wyrazy są zapisywane za pomocą ciągów znaków. Początek takiego ciągu składa się z symboli pełniących funkcje znaków fonetycznych odpowiadających zbiorom spółgłosek (samogłoski nie są zapisywane). Ostatni symbol jest znakiem dookreślającym (fachowo nazywanym znakiem determinatywnym), który określa kategorię słowa. W sytuacji gdy ten sam zapis fonetyczny może odnosić się do kilku różnych słów, dodanie informacji o kategorii danego słowa ułatwia jego odczytanie.
Odczytując hieroglify, podobnie jak w przypadku czytania wykresów, sens słowa otrzymujemy, składając znaczenia i wspólne relacje składowych symboli. Nie interpretujemy jednak bezpośrednio symboli na wykresie, ale odczytujemy przypisane im znaczenia lub dźwięki. Aby zrozumienie przekazu było możliwe, reguły zapisu i znaczenie symboli, czyli kod jakim się posługujemy, muszą być znane nadawcy i odbiorcy. W przypadku egipskich hieroglifów kierunek czytania jest określony przez stronę, w którą zwrócone są symbole. Napis można odczytywać z lewej do prawej lub z prawej do lewej, w zależności od tego, czy symbole w napisie zwrócone są w lewo czy w prawo.
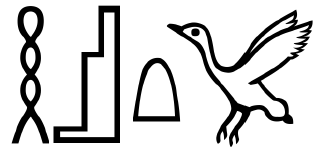 Rysunek 4: Zapis staroegipskiego słowa “zniknąć”. Zapis z użyciem hieroglifów składa się z trzech znaków: “knot”, “krzesło”, “bochenek”, odpowiadających kolejno dźwiękom/zbitkom spółgłosek: “h”, “htm”, “t”. Po tych znakach występuje znak determinatywny “lecący ptak”. Określa on zarówno kategorię zapisywanego wyrazu, jak i kierunek czytania. W prezentowanym przypadku wyraz czytamy od lewej do prawej, a więc w stronę przeciwną do kierunku, w który zwrócony jest symbol ptaka.
Źródło: opracowanie z użyciem kroju pisma JSesh
Rysunek 4: Zapis staroegipskiego słowa “zniknąć”. Zapis z użyciem hieroglifów składa się z trzech znaków: “knot”, “krzesło”, “bochenek”, odpowiadających kolejno dźwiękom/zbitkom spółgłosek: “h”, “htm”, “t”. Po tych znakach występuje znak determinatywny “lecący ptak”. Określa on zarówno kategorię zapisywanego wyrazu, jak i kierunek czytania. W prezentowanym przypadku wyraz czytamy od lewej do prawej, a więc w stronę przeciwną do kierunku, w który zwrócony jest symbol ptaka.
Źródło: opracowanie z użyciem kroju pisma JSesh
Wykresy statystyczne także używają abstrakcyjnych znaków i symboli, których kształt, kolor, wielkość, położenie, liczba mają często niedosłowne, symboliczne znaczenie. Znaczenie to powinno być zrozumiałe dla odbiorcy, dlatego też do wykresów zwykle dodaje się legendę z wyjaśnieniami kodu. Przedstawiając informację w bardziej abstrakcyjny sposób, prezentując wielkości za pomocą położenia w układzie współrzędnych czy poprzez wielkość obiektu, korzystamy z niedosłownych znaczeń. Powinniśmy więc upewnić się, że odbiorca właściwie odczyta nasze intencje. Przykładowo, korzystając z kolorów, należy mieć na uwadze, że w różnych częściach świata kolorom przypisane są odmienne znaczenia
Jeżeli będziemy używać symboli niezrozumiałych dla odbiorcy, możemy stworzyć wykres równie trudny do odczytania co egipskie hieroglify dla większości współczesnych ludzi.
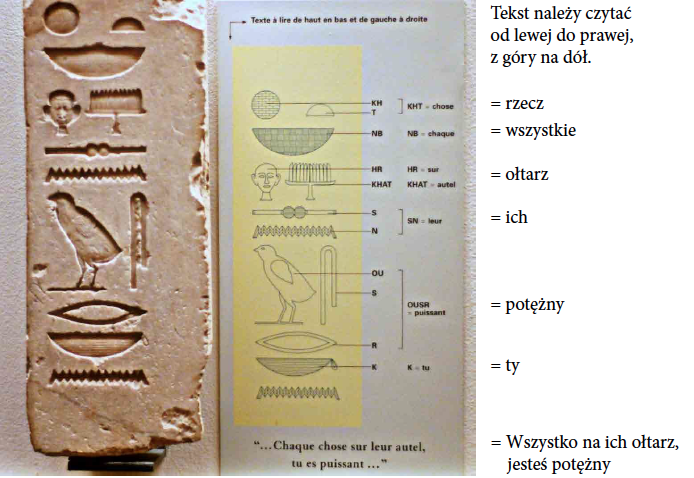
Rysunek 5: Zapis z użyciem hieroglifów zdania “Wszystko na ich ołtarz, jesteś potężny”. Zdjęcie eksponatu z muzeum Luwr, sala starożytnego Egiptu. Wrażenie robi precyzja, z jaką wykonany jest każdy symbol. Źródło: opracowanie na bazie zdjęcia
Czasem, aby wykonać interesującą wizualizację danych, musisz być prawdziwym człowiekiem renesansu...
Piękno kryje się w wizualizacjach, które prezentują informację nieznaną uprzednio odbiorcy, w taki sposób, który pozwoli tę nieznaną prawdę odkryć i łatwo ją zapamiętać. Ważne, aby prezentacja taka była ciekawa, odbiorca przecież musi chcieć odkrywać, prawda? Osoby stosujące techniki skutecznego zapamiętywania wiedzą, jak pomocne może być odpowiednie graficzne przedstawienie informacji, nawet jeżeli ta wizualizacja będzie miała miejsce wyłącznie w głowie. Często łatwiej jest zapamiętać obraz, z którego można odczytać proporcje, niż zapamiętać te same proporcje w ich abstrakcyjnej liczbowej postaci.
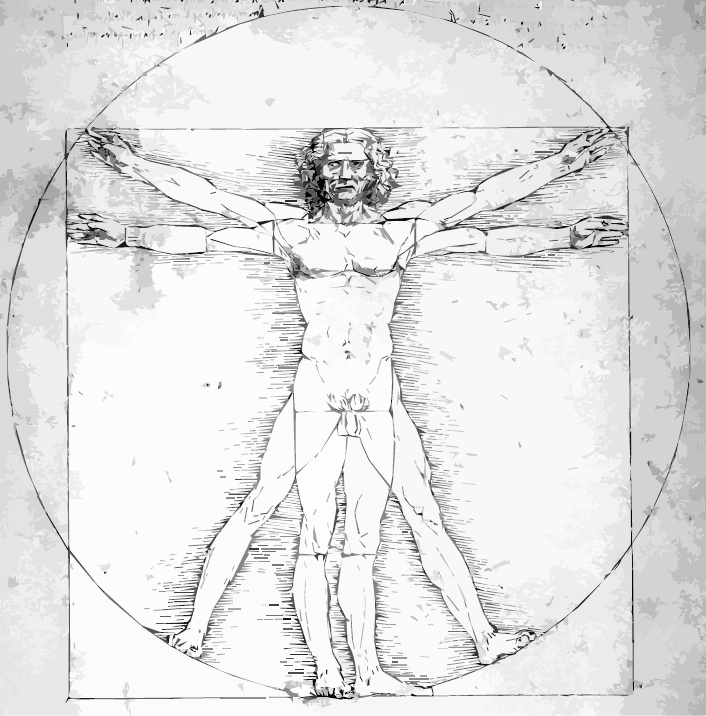
Świetną ilustracją tego faktu jest bardzo oryginalna wizualizacja, którą opracował mistrz renesansu Leonardo da Vinci (1452–1519). Chodzi mi o rysunek o nazywie Człowiek witruwiański, który otwiera ten esej. Żyjący w czasach Leonarda da Vinci i wcześniejszych mieli problemy ze zrozumieniem proporcji ciała idealnie zbudowanego człowieka. Uważając sylwetkę ludzką za przejaw doskonałości, próbowali wpisać ją w obrys katedry lub zamku. Aby docenić dzieło Leonarda da Vinci, trzeba najpierw zobaczyć, jak nieudolnie proporcje ludzkiego ciała przedstawiali jemu współcześni. Do jednych z bardziej udanych prób tamtej epoki zaliczyć można szkice architekta Francesca di Giorgio, które z dzisiejszej perspektywy są dalekie od doskonałości.
Ilustracja Leonarda da Vinci odwołuje się do księgi rzymskiego architekta Witruwiusza, według którego wysokość idealnie zbudowanego człowieka odpowiada szerokości rozłożonych ramion. Ponadto długość stopy dorosłego mężczyzny to 1/7 wysokości człowieka, a długość łokcia to 1/4 tej wysokości. Sylwetkę człowieka można podzielić w pionie na cztery równe części, których granice przebiegają na wysokości kolan, podbrzusza i piersi. Wysokość człowieka i długości jego kończyn można również wyrazić jako wielokrotności długości jego ramion, nadgarstka, łokcia czy barku. Ale jak przedstawić to bogactwo wzajemnych zależności pomiędzy długościami części ciała? Patrząc na szkic Człowiek witruwiański autorstwa Leonarda da Vinci, dostrzeżemy te wszystkie proporcje i zależności. Czyż nie jest to interesująca ilustracja ukazująca zależności dla wielu jemu współczesnych, jak również wielu z nas nieznane? Intuicyjnie wydawać by się mogło, że rozpiętość ramion jest mniejsza niż wysokość człowieka, a tymczasem proste pomiary pokazują, że dla większości osób ta różnica nie przekracza kilku centymetrów.
Aby wykonać taką bogatą w szczegóły i zależności wizualizację, autor musiał znać dzieła architektów, w tym Witruwiusza, znać anatomię człowieka, musiał potrafić prezentować graficznie informację oraz mieć dużą wyobraźnię. Musiał być prawdziwym człowiekiem renesansu.
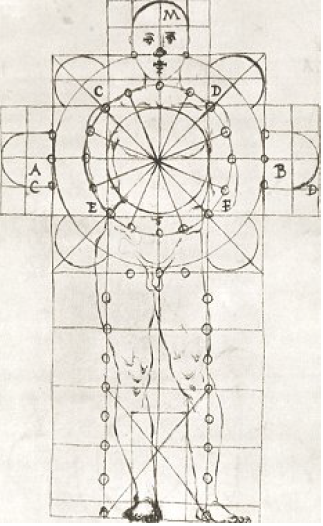 Rysunek 6: Próba przedstawienia proporcji ludzkiego ciała przez architekta Francesca di Giorgio w 1470 roku. Źródło: Wikipedia, domena publiczna
Rysunek 6: Próba przedstawienia proporcji ludzkiego ciała przez architekta Francesca di Giorgio w 1470 roku. Źródło: Wikipedia, domena publiczna
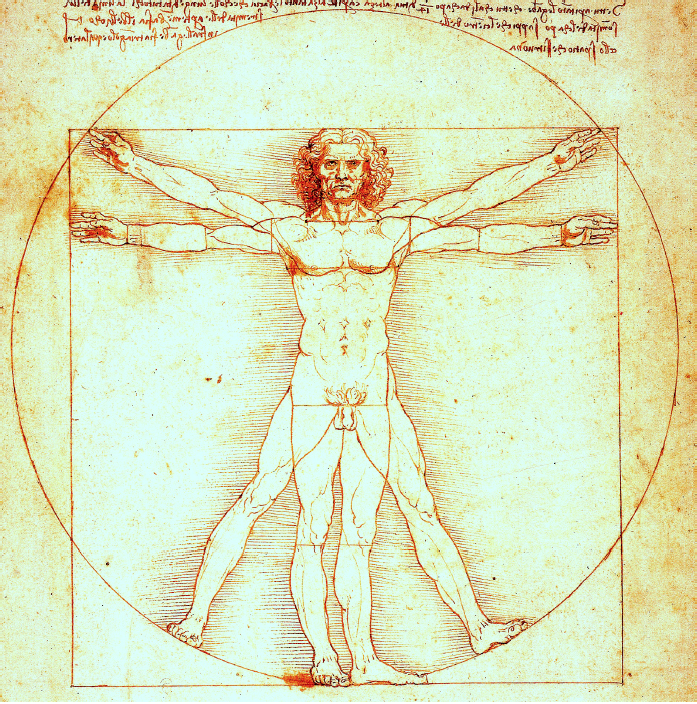
Rysunek 7: Człowiek witruwiański autorstwa Leonarda da Vinci. Galleria dell' Accademia, Wenecja (1485–90). Wpisanie sylwetki mężczyzny w kwadrat pozwala przedstawić rozpiętość ramion i wysokości. Wpisanie w okrąg pozwala pokazać zasięg ramion podniesionych do góry i odchylonej nogi, liniami pomocniczymi zaznaczono długości poszczególnych elementów ciała. Wzrost podzielono na cztery równe części, dzięki czemu łatwiej zauważyć, że głowa jest szóstą częścią wysokości, stopa siódmą, długość łokcia i odległość kolana od stopy są czwartą częścią wysokości. Źródło: Wikipedia, domena publiczna
..albo oświecenia
Przenieśmy się teraz o następne trzy stulecia, w czasy oświecenia, aby przyjrzeć się bardzo ciekawemu wykresowi, który opracował teolog, filozof i chemik Joseph Priestley (1733–1804).
Joseph Priestley zasłynął między innymi jako odkrywca tlenu, ale w naszej wędrówce po historii bardziej interesujące będzie inne jego dokonanie, mianowicie wykres prezentujący dane w awangardowy, jak na tamte czasy, sposób.
Wykres ten zyskał olbrzymią popularność, od razu był uznany za przełomowy i niewątpliwie stanowił inspirację dla innych osób zainteresowanych prezentacją danych. W czasach Priestleya taka prezentacja danych była prawdziwą rewolucją. Na niewielkiej przestrzeni przedstawiono informację o okresach życia znanych mężów stanu. Z wykresu można natychmiast odczytać, kto był komu współczesny, kto mógł być czyim uczniem, kto z kim mógł utrzymywać kontakty. Jeżeli data urodzin lub śmierci była nieznana, to na wykresie jest to zaznaczone w ciekawy sposób z użyciem kropkowanej linii.
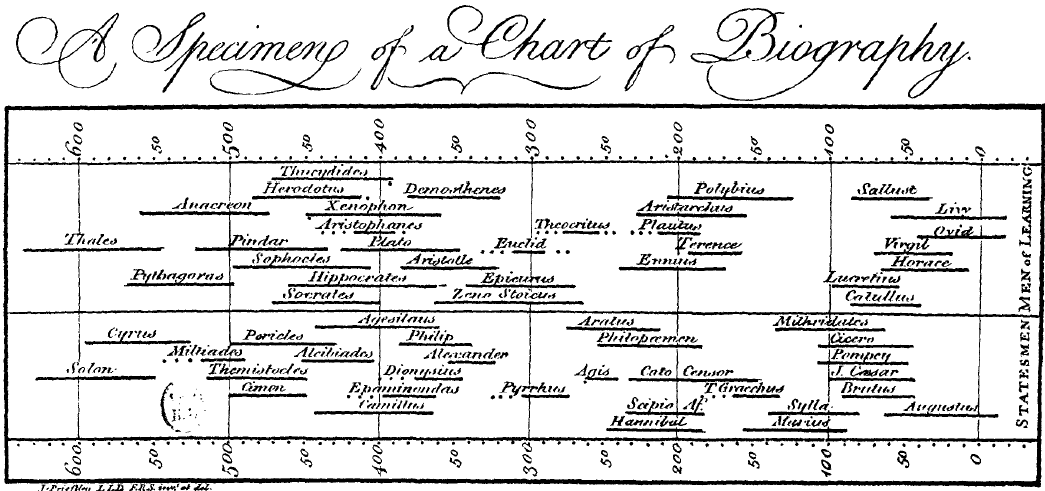 Rysunek 8: Wykres prezentujący okresy życia polityków, mężów stanu (poniżej poziomej linii) oraz ludzi nauki (powyżej poziomej linii). Chart of Biography Josepha Priestleya (1765). Źródło: Wikipedia, domena publiczna
Rysunek 8: Wykres prezentujący okresy życia polityków, mężów stanu (poniżej poziomej linii) oraz ludzi nauki (powyżej poziomej linii). Chart of Biography Josepha Priestleya (1765). Źródło: Wikipedia, domena publiczna
Przedstawianie danych wzdłuż linii czasu (ang. timeline) od momentu zaprezentowania swojego wykresu przez Priestleya cieszyło się niemalejącą popularnością. Nieraz metoda ta znajdywała efektowne zastosowania. Na przykład kilka lat temu odkrył ją na nowo dla swoich potrzeb portal społecznościowy Facebook, a za nim inne tego typu serwisy.
Zainteresowany tym sposobem prezentacji, zastosowałem podobny format do przedstawienia daty pierwszej publikacji lektur szkolnych, napisanych po roku 1700. Zaznaczyłem okresy życia autorów tych lektur, przez co można odczytać ile lat miał autor gdy ukończył pisanie danego dzieła oraz jacy inni autorzy byli mu współcześni.
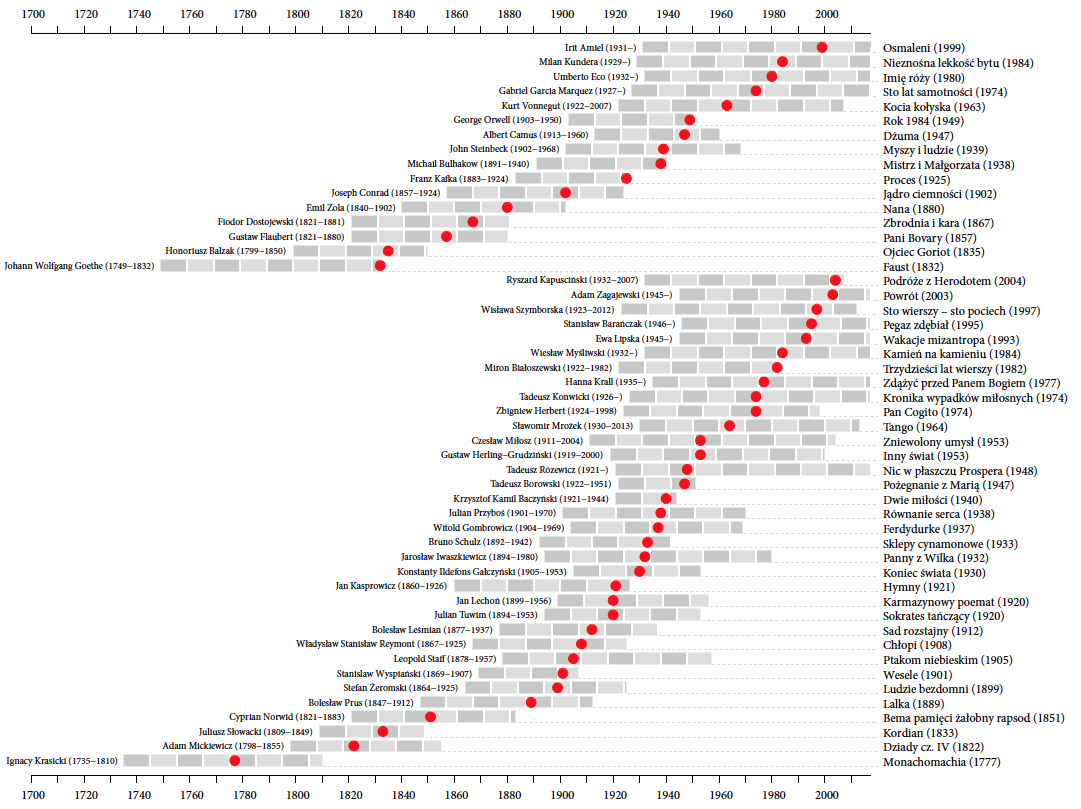 Rysunek 9: Lektury obowiązkowe w liceum z okresu od oświecenia do literatury współczesnej. Na górnym panelu przedstawiono dzieła wydane po raz pierwszy w języku innym niż polski, na dolnym panelu dzieła wydane oryginalnie w języku polskim. Czerwoną kropką zaznaczono daty publikacji danego dzieła. Szarymi prostokątami zaznaczono okres życia autora określonej lektury. Pełen prostokąt odpowiada okresowi 10 lat. Źródło: opracowanie własne
Rysunek 9: Lektury obowiązkowe w liceum z okresu od oświecenia do literatury współczesnej. Na górnym panelu przedstawiono dzieła wydane po raz pierwszy w języku innym niż polski, na dolnym panelu dzieła wydane oryginalnie w języku polskim. Czerwoną kropką zaznaczono daty publikacji danego dzieła. Szarymi prostokątami zaznaczono okres życia autora określonej lektury. Pełen prostokąt odpowiada okresowi 10 lat. Źródło: opracowanie własne
Czasem data publikacji kryje w sobie ciekawą historię, którą można opowiedzieć, używając tego wykresu jako tła. Przykładowo Franz Kafka pisał do szuflady, prosząc w testamencie przyjaciela Maxa Broda o spalenie notatek po jego śmierci. Ten jednak jego woli nie posłuchał i dziś Proces jest lekturą, ale opublikowaną już po śmierci autora. W przypadku Fausta Johanna Wolfganga Goethego data publikacji jest momentem zakończenia opracowania dzieła, które autor tworzył przez całe dorosłe życie. Dyskusyjne może być uznanie Josepha Conrada za obcokrajowca, jest to bowiem pseudonim Józefa Teodora Konrada Korzeniowskiego, który był Polakiem i czuł się Polakiem, ale publikował w języku angielskim, dlatego został umieszczony w górnym panelu tego wykresu.
Taką pomoc dydaktyczną poloniści mogą używać jako szkielet do omawiania wpływu dzieł jednych autorów na innych.
Dane to abstrakcja rzeczywistości, a wizualizacja danych to abstrakcja abstrakcji
W naszej wędrówce po kolejnych epokach graficzne reprezentacje informacji stają się coraz bardziej abstrakcyjne. Aby poprawnie odczytać prezentowany przekaz, odbiorca musi znać pewne fakty dotyczące obiektów użytych na wykresie, np. okręgu, kwadratu czy też kartezjańskiego układu współrzędnych.
Wykres danych to abstrakcja danych. Element abstrakcji w wizualizacji jest na tyle istotny, że za ojca statystycznej wizualizacji danych uznaje się dopiero Szkota Williama Playfaira (1759–1823). Playfair pracował w wielu zawodach, co w oświeceniu nie było aż tak niespotykane wśród ludzi wykształconych. Pracował jako inżynier, budowniczy młynów, złotnik, statystyk, pisał też dzieła poświęcone ekonomii politycznej. W 1786 roku opublikował The Commercial and Political Atlas, dzieło, w którym przedstawił różnorodne dane o wymianie dóbr pomiędzy państwami. Dla zwiększenia czytelności dane zamieszczone w tabelach zilustrował dodatkowo za pomocą 43 wykresów szeregów czasowych oraz jednego wykresu paskowego.
Ten wykres paskowy był dla jemu współczesnych czymś zupełnie nowym. Znane były prezentacje danych pokazujące jak określone wartości zmieniają się w czasie (wykresy czasowe) lub jak zależą od położenia geograficznego (kartogramy). Wykres paskowy jest abstrakcją danych bez wykorzystania metafory rzeczywistych obiektów. Z tego powodu jest uznawany jako przykład pierwszej grafiki statystycznej opublikowanej w dużym dziele.
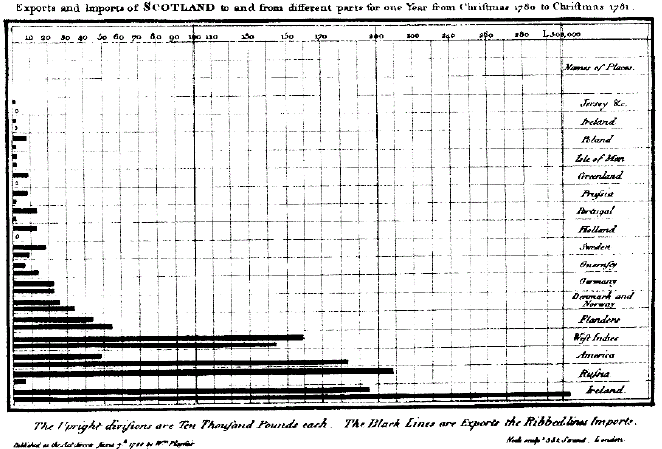
Na wykresie paskowym dane są przedstawione za pomocą długości, co wymaga od czytelnika zrozumienia abstrakcyjnej reprezentacji liczb. Ale po opanowaniu tego kodu, ta graficzna reprezentacja liczb jest dużo czytelniejsza niż tabela pełna cyfr. Obecnie wykresy paskowe są w powszechnym użyciu, są umieszczane w podręcznikach i artykułach. Jestem przekonany, że każdy z Czytelników miał nie raz z nimi kontakt.
Rysunek 10: Wykres paskowy z The Commercial and Political Atlas Williama Playfaira. Przedstawia wielkość importu oraz eksportu pomiędzy Szkocją a jej handlowymi partnerami. Największym partnerem handlowym w tym czasie była Irlandia. Źródło: Wikipedia, domena publiczna
Williama Playfaira uznaje się też za wynalazcę wykresu kołowego. Pierwszy taki wykres można znaleźć w dziele The Statistical Breviary, opublikowanym w 1801 roku. Dziś ta metoda prezentacji danych cieszy się wśród statystyków złą sławą, ponieważ jest nagminnie nadużywana w sytuacjach, w których dane można pokazać znacznie czytelniej, korzystając z innych dostępnych wykresów. Nie sposób jednak nie docenić znaczenia tej formy prezentacji danych. Od czasu jej wynalezienia, na początku XIX wieku, była wykorzystywana wielokrotnie i w niektórych środowiskach jest postrzegana jako znak rozpoznawczy statystyki stosowanej.
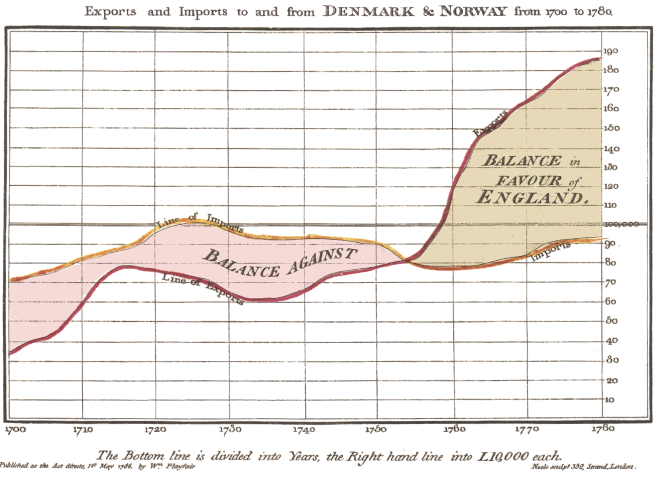
Playfair znany był z opinii, że wykresy przedstawiają dane znacznie lepiej niż tabele. Dawał upust temu przekonaniu, okraszając swoje dzieła licznymi wykresami, podziwianymi ze względu na ich przemyślany projekt, umożliwiający szybkie przekazanie kluczowych faktów. Przykładem może być poniższy rysunek, prezentujący bilans pomiędzy eksportem a importem Anglii. Nie jest potrzebny żaden dodatkowy komentarz, aby odbiorca miał od razu ogólne pojęcie o tym, jak kształtowała się wielkość eksportu i importu i wzajemny bilans na przestrzeni kilkudziesięciu lat.
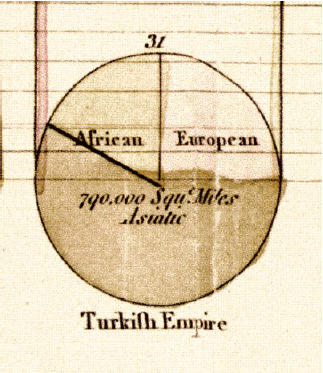 Rysunek 11: Wykres kołowy z The Statistical Breviary Williama Playfaira, przedstawia względną wielkość europejskiej, afrykańskiej i azjatyckiej części Imperium Osmańskiego. Źródło: Wikipedia, domena publiczna
Rysunek 11: Wykres kołowy z The Statistical Breviary Williama Playfaira, przedstawia względną wielkość europejskiej, afrykańskiej i azjatyckiej części Imperium Osmańskiego. Źródło: Wikipedia, domena publiczna
Takiemu wykresowi może towarzyszyć tabela lub opis, pozwalające na szczegółowe odczytanie wysokości importu i eksportu w kolejnych latach. Ale już sam wykres tworzy w naszym umyśle szkielet tego, co znajdziemy w danych. Natychmiast widzimy, że import przez prezentowane 80 lat pozostawał na podobnym poziomie, podczas gdy eksport rósł, szczególnie szybko w dwóch okresach: 1700–1715 i 1755–1775, gdy to przekroczył poziom importu.
Rysunek 12: Wykres bilansu z The Commercial and Political Atlas Williama Playfaira. Przedstawia wielkość angielskiego importu i eksportu, a także bilans tych dwóch wartości. Źródło: Wikipedia, domena publiczna
Wykres pozwala na zobaczenie tego, czego nie zobaczymy w tabeli liczb
Powyższe grafiki miały charakter sprawozdawczy. Opisywały, jak rzeczy wyglądały w mniej lub bardziej odległej przeszłości. Ale wykresy mogą się również znacznie przysłużyć zupełnie nowym odkryciom naukowym i społecznym. Ciekawym przykładem grafiki statystycznej towarzyszącej naukowej rewolucji jest wykres opracowany przez lekarza dr. Johna Snowa (1813–1858) dotyczący epidemii cholery w londyńskim Soho w 1854 roku. O istotnej wadze tego dzieła świadczy między innymi to, że dzięki wynikom z pracy nad tą epidemią John Snow jest uznawany za prekursora epidemiologii.
Nakreślmy kontekst. Jest 1854 rok, liczba mieszkańców dzielnicy londyńskiego Soho szybko rośnie. Dzielnica nie ma kanalizacji. Nieczystości przechowywane są w szambach mieszczących się w piwnicach. Niestety szamba nie są wystarczająco duże jak na potrzeby szybko rosnącej liczby mieszkańców i zbyt szybko się przepełniają. Władze Londynu nakazują je częściej opróżniać przez wylanie zawartości do Tamizy. W Londynie niedługo wybucha epidemia cholery, która w ciągu pierwszego miesiąca zabija przeszło 120 osób, a łącznie ofiar jest ponad 600. Zaraza spowodowała taką panikę, że jedna trzecia mieszkańców Soho uciekła z miasta w obawie o swoje życie.
W tamtych czasach wierzono, że cholera jest rozprzestrzeniana przez “morowe powietrze”. Przypomnijmy, że bakterie wywołujące choroby odkrył Louis Pasteur dopiero 7 lat później, zatem tak podczas tej epidemii jak i wcześniejszych ludzie naprawdę nie mieli pojęcia z czym tak naprawdę mają do czynienia. Nasz bohater, John Snow, szukając przyczyny epidemii, rozmawiał z mieszkańcami opanowanej chorobą dzielnicy. Odkrył, że wszystkie przypadki zachorowań i śmierci są związane z pompą wody na Broad Street. Zgony dotyczyły głównie osób mieszkających w tej okolicy albo dzieci uczęszczających do szkoły w pobliżu, albo osób mieszkających dalej, ale pobierających wodę z tego ujęcia. Zauważył to dzięki naniesieniu na mapę dzielnicy punktów symbolizujących zachorowanie danej osoby w miejscu jej zamieszkania/pracy/szkoły.
John Snow nie potrafił wytłumaczyć, co dokładnie tę chorobę wywołuje, ale zebrane dowody wystarczyły, by przekonać władze Londynu do zamknięcia wskazanego ujęcia wody. Jak przyznawał sam Snow, epidemia była już wtedy w fazie końcowej i nie sposób przypisać definitywnego zakończenia epidemii wyłącznie tej decyzji. Z pewnością jednak ograniczyło to liczbę przypadków śmiertelnych i przyczyniło się do lepszego zrozumienia przyczyn epidemii. Później udało się ustalić, że roznosząca zarazki pompa wody była położona bardzo blisko jednego z szamb.
 Rysunek 13: Portret Johna Snowa. Źródło: Wikipedia, domena publiczna
Rysunek 13: Portret Johna Snowa. Źródło: Wikipedia, domena publiczna
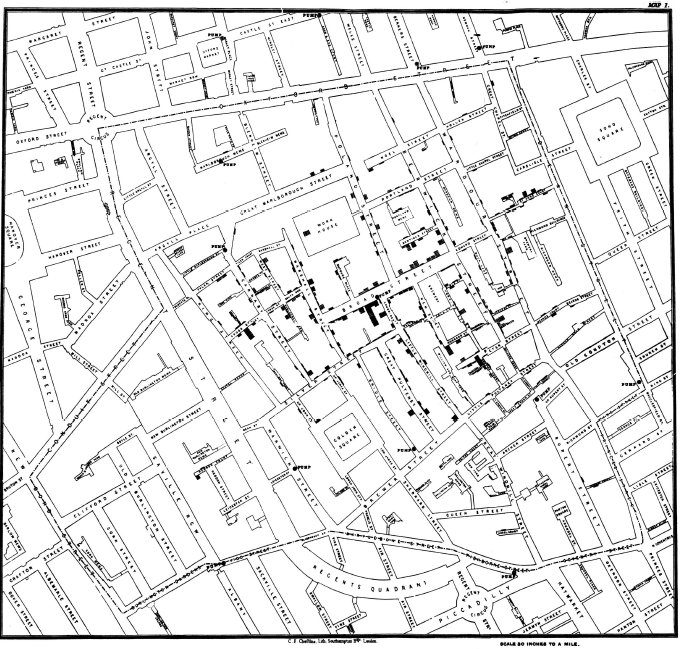
Rysunek 14: Wykres, który przeszedł do historii jako dowód na źródło epidemii cholery w londyńskim Soho. Mapa została opracowana przez Johna Snow, ale narysował ją i wydrukował litograf John Churchill. Źródło: On the Mode of Communication of Cholera, 2nd Ed., John Churchill, New Burlington Street, London, England, 1855
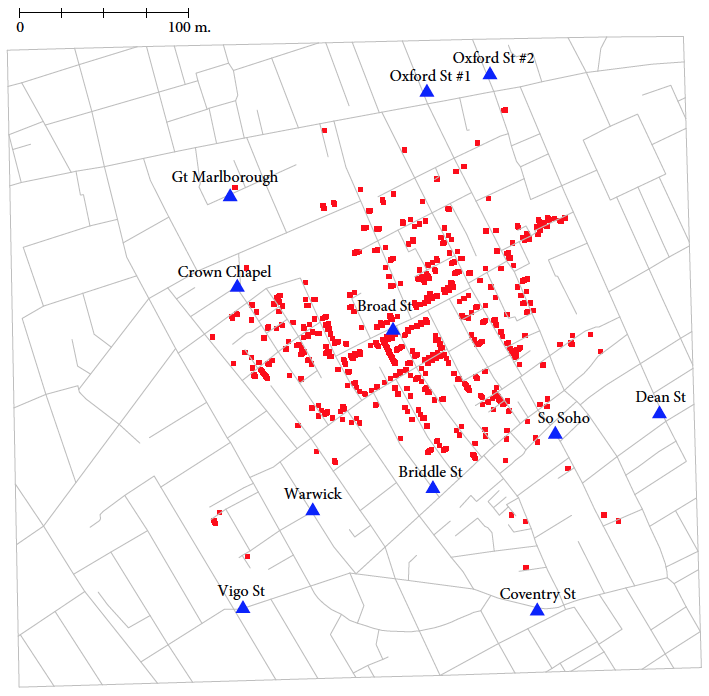
Mapa przedstawiona na rysunku 14 i jej rekonstrukcja przedstawiona na rysunku 15, opracowana na podstawie pakietu HistData [Michael Friendly. Histdata: Data sets from the history of statistics and data visualization, 2013], stanowi piękny przykład tego, jak wizualizacja danych pozwala na dobitne przedstawienie związku pomiędzy różnymi czynnikami, w tym przypadku zgonami a ujęciem wody. W przypadku Snowa można przypuszczać, że to właśnie proces tworzenia pierwszej wersji mapy pomógł odkryć mu źródło epidemii.
Rysunek 15: Rekonstrukcja wykresu Snowa. Czerwone punkty przedstawiają miejsca zamieszkania ofiar cholery, niebieskie trójkąty przedstawiają położenie ujęć wody. Wyraźnie widać związek pomiędzy odległością od ujęcia wody na Broad St. a miejscem zamieszkania ofiar epidemii.
Wykres opracowano z użyciem danych z pakietu HistData. Źródło: opracowanie na bazie dokumentacji
Grafika statystyczna jako środek perswazji
Jak zobaczyliśmy na przypadku epidemii cholery, grafika statystyczna jest bardzo przydatna przy dokonywaniu odkryć naukowych i badania różnych zjawisk zachodzących w świecie. Poniżej okaże się, że może być również użyta jako narzędzie do wywierania wpływu na opinię odbiorcy i w konsekwencji na jego dalsze decyzje.
Najbardziej znanym przykładem grafiki statystycznej użytej w celu wywołania konkretnej reakcji, a wręcz wykorzystanej jako środek silnej perswazji, były wykresy angielskiej pielęgniarki i jednocześnie statystyka Florence Nightingale (1820–1910).
W tej historii niemałą rolę odgrywa osobowość panny Nightingale, zacznijmy więc od jej krótkiego przedstawienia. Kobieta wywodząca się z tzw. dobrego domu (była arystokratką) przeraziła całą rodzinę, gdy oświadczyła, że chce zostać pielęgniarką. W tamtych czasach absolutnie nie było to zajęcie dla kobiet z wysokich czy choćby średnich warstw społecznych. Nightingale nie była jednak osobą, która łatwo rezygnuje ze swoich planów. Nie dosyć, że została przełożoną pielęgniarek, to jeszcze w wieku 33 lat rozpoczęła organizację opieki szpitalnej podczas wojny krymskiej
 Rysunek 16: Portret Florence Nightingale. Źródło: Wikipedia, domena publiczna
Rysunek 16: Portret Florence Nightingale. Źródło: Wikipedia, domena publiczna
Pracowała bez wystarczających środków medycznych, zaopatrzeniowych czy żywieniowych. Robiła, co mogła, by pomóc rannym żołnierzom. Znana była z tego, że wykonywała systematycznie obchody po korytarzach szpitala, niosąc lampę, przez co przylgnęło do niej określenie “the Lady with the lamp”. Czy robiła to, by żołnierze nie czuli się samotni i opuszczeni w nocy, sam na sam z bólem i cierpieniem? Jej postawa przerodziła się w symbol, sto lat później nakręcono film pod tytułem The Lady with the Lamp, a nawiązania do niej pojawiają się w poezji Henry’ego Longfellowa i innych poetów
Dała się poznać jako bardzo zdeterminowana osoba. Jednocześnie należy podziwiać jej podejście do pracy, nie zajmowała się tylko doraźną pomocą, ale interesował ją całokształt problemu i zależało jej na stworzeniu dobrych systemowych rozwiązań, tak aby z jej doświadczeń mogli korzystać również inni.
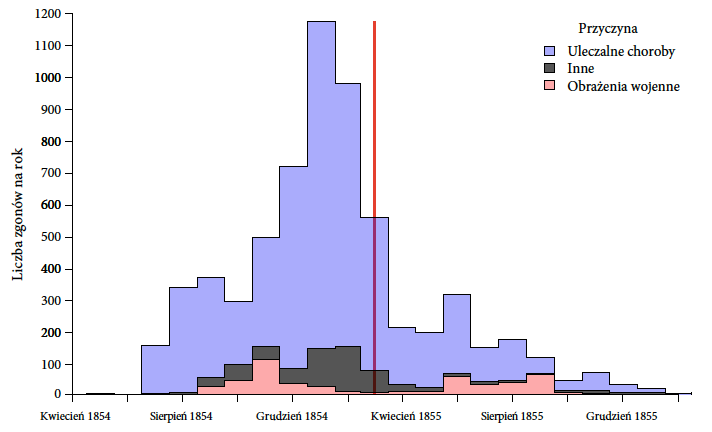
W okresie służby na Krymie Nightingale odkryła, że większość żołnierzy ginie z powodu złej opieki szpitalnej: zakażeń, niedożywienia i innych przyczyn, którym można zaradzić, organizując lepszą opiekę. Oszacowała, że z 18 tysięcy zgonów około 16 tysięcy było spowodowanych zakażeniami, a więc niskim poziomem higieny i osłabieniem chorego spowodowanym brakiem żywności i niedostatecznym wyposażeniem szpitali polowych. To odkrycie niosło jednocześnie jasną przesłankę, co zrobić, by znacząco ograniczyć liczbę ofiar – należało lepiej zorganizować opiekę szpitalną. Dziś to oczywiste, ale w tamtych czasach było rewolucyjnym odkryciem.
Aby przedstawić swoje racje, Florence opracowała wykres polarny (nazywany też różą Nightingale, ang. Nightingale rose diagram) przedstawiony na rysunku 17, przez samą autorkę określany wykresem grzebieniowym (ang. coxcomb).
Z opracowanego przez Nightingale wykresu łatwo odczytać, jak wiele śmierci spowodowanych było uleczalnymi chorobami (zakażenia szpitalne, efekt niedożywienia lub słabej opieki szpitalnej). Kolor niebieski, wskazujący śmiertelne przypadki, którym można było zapobiec lepszą opieką, dominuje cały wykres. Takich zgonów, którym można było zapobiec, jest wyraźnie więcej niż zgonów spowodowanych ranami wojennymi.
In the great history of the land,
A noble type of good,
Heroic womanhood ... Santa Filomena,
Henry Wadsworth Longfellow
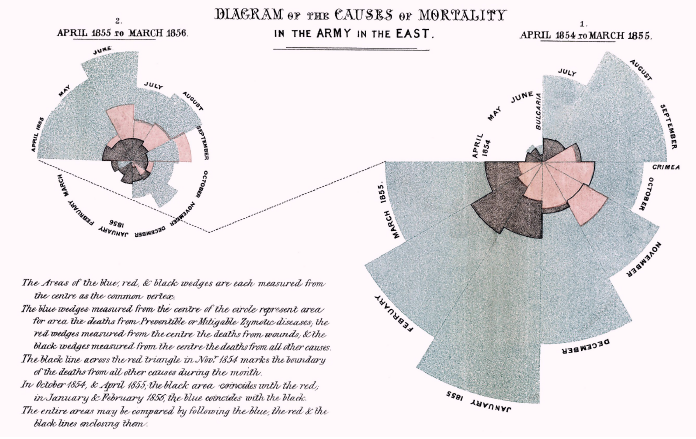
Rysunek 17: Wykres przedstawia liczbę zgonów spowodowanych przez uleczalne choroby (niebieski), rany wojenne (czerwony) i inne przyczyny, np. odmrożenia (czarny). Liczba zgonów jest proporcjonalna do promienia segmentu. Źródło: Diagram of the causes of mortality in the army in the East, opublikowany w Notes on Matters Affecting the Health, Efficiency, and Hospital Administration of the British Army, wysłany do królowej brytyjskiej w 1858 roku. Źródło: domena publiczna
Wykres ten nie tylko pokazywał, co jest złego w systemie opieki szpitalnej na polu bitwy, ale połączony był z jasną sugestią autorki, że poprawa opieki szpitalnej doprowadzi do znacznego ograniczenia liczby ofiar wojennych.
Dzięki prostej formie, dobitnie przestawiającej fakty, był dla wszystkich wystarczająco zrozumiały. Wykres spełnił swoją rolę bardzo dobrze, był edukacyjny i informacyjny (przedstawił nowe fakty), plus był opiniotwórczy (dzięki wadze przedstawianych informacji), dlatego doprowadził do zmian po myśli Nightingale. Warunki w opiece szpitalnej znacznie się poprawiły. W tym przypadku, bez żadnego nadużycia można stwierdzić, że to grafika statystyczna, czytelne i celowe przedstawienie danych, doprowadziło do uratowania tysięcy ludzkich istnień i do znaczących zmian w systemie opieki nad chorymi.
Rysunek 18: Inna prezentacja danych zebranych przez Florence Nightingale.
Wykres opracowano z użyciem danych z pakietu HistData. Źródło: opracowanie własne
Za swoje zasługi Florence Nightingale w 1907 roku, jako pierwsza kobieta w historii, otrzymała Brytyjski Order Zasługi
Sztuką jest przedstawić złożone, wielowymiarowe zjawisko w prosty i czytelny sposób
Wykresy Williama Playfaira są pięknymi przykładami wizualizacji danych o ekonomii państwa, wykres Johna Snowa pokazuje, jak dzięki wizualizacji danych można odnaleźć wspólny mianownik dziesiątek zgonów, a wykresy Florence Nightingale prezentują moc perswazji dobrze zaprojektowanej grafiki. Przyjrzyjmy się teraz wykresowi, o którym Edward Tufte (którego jeszcze spotkamy w jednym z kolejnych przystanków naszej wędrówki przez dzieje wizualizacji) napisał, że jest to “być może najlepsza grafika statystyczna, jaka kiedykolwiek powstała”.
Zacznijmy od przedstawienia autora. Charles Minard (1781–1870) był francuskim inżynierem lądowym, a także pionierem, jeżeli chodzi o zastosowania grafiki w inżynierii i statystyce. W 1869 roku opublikował mapę przedstawiającą historię napoleońskiej inwazji na Rosję w latach 1812–13. Piękno tej grafiki bierze się z prostoty i elegancji zaprezentowania złożonych i wielowymiarowych danych.
Dziesiątki bitw i potyczek, ruchy olbrzymich mas wojsk, wyniki starć z wrogimi wojskami – to wszystko można odczytać z jednej mapy. Liczebność armii na poszczególnych etapach inwazji przedstawiono za pomocą grubości odcinków łączących poszczególne istotne punkty kampanii. Na linii Kowna armia Napoleońska liczyła 420 tysięcy żołnierzy. Po drodze do Moskwy od głównej armii oddzieliły się dwie mniejsze dywizje, a dalej na wschód doszło do szeregu bitew, w wyniku których wielkość armii topniała, co pokazuje zwężająca się szerokość brązowej wstęgi. Do Moskwy dotarło jedynie około 100 tysięcy żołnierzy. Byli to jednak żołnierze bez wystarczającego zaopatrzenia, ponieważ wycofująca się armia rosyjska nie pozostawiła żadnych zapasów żywności.
 Rysunek 19: Mapa przedstawia losy armii napoleońskiej na różnych etapach inwazji na Rosję.
Źródło: Charles Minard Figurative Map of the successive losses in men of the French Army in the Russian campaign 1812–1813, rok 1869. Źródło: domena publiczna
Rysunek 19: Mapa przedstawia losy armii napoleońskiej na różnych etapach inwazji na Rosję.
Źródło: Charles Minard Figurative Map of the successive losses in men of the French Army in the Russian campaign 1812–1813, rok 1869. Źródło: domena publiczna
Odwrót rozpoczął się 18 października z powodu braku żywności i zbliżającej się zimy. Na wykresie odwrót zaznaczony jest czarną wstęgą, której jednocześnie towarzyszy prezentacja spadającej temperatury (w dolnej części grafiki). Żołnierzom nie udało się uciec przed zimą i zimnem, podczas odwrotu temperatura spadła do -30 stopni. Temperatura, brak żywności, potyczki z wrogiem spowodowały, że w drodze powrotnej do Kowna armia stopniała do 30 tysięcy żołnierzy. Niewielki ułamek początkowej armii.
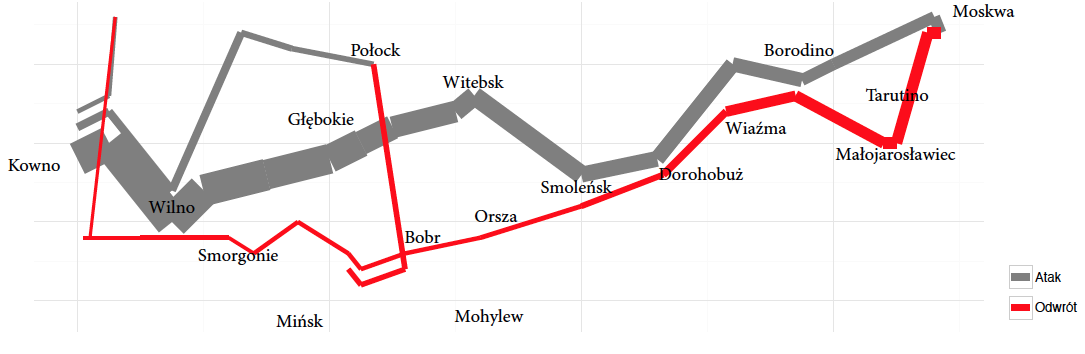 Rysunek 20: Rekonstrukcja informacji przedstawionych na mapie Minarda dotyczących pozycji i liczebności wojsk podczas ataku i odwrotu spod Moskwy.
Rysunek 20: Rekonstrukcja informacji przedstawionych na mapie Minarda dotyczących pozycji i liczebności wojsk podczas ataku i odwrotu spod Moskwy.
Wykres opracowano z użyciem danych z pakietu HistData. Źródło: opracowanie na bazie dokumentacji
Zaznaczając położenie wojsk, uwzględniono nie tylko położenie geograficzne, ale również daty osiągnięcia przez armię danej pozycji. Umożliwia to śledzenie w czasie przemieszczania się cesarskiego wojska jak i przebieg bitew (zwężająca się wstęga oznacza coraz to mniejszą liczbę żołnierzy po kolejnych krwawych potyczkach). Zaznaczona spadająca temperatura podczas odwrotu (a inwazja miała miejsce podczas ponoć jednej z najsroższych zim w historii) ułatwia zrozumienie, z jakimi innymi przeszkodami musieli się zmierzyć żołnierze, w dużej części pochodzący z południa Europy.
Mapa Minarda podważa twierdzenia, że każda dobra wizualizacja musi być prosta i natychmiast czytelna. Jest przykładem, że bogata w różnorodne informacje grafika wcale nie musi być tablicą rozdzielczą (ang. dashboard) złożoną z wielu prostych wykresów.
Dzieło Minarda wcale nie jest prostą grafiką. Zawiera wiele szczegółów, które można stopniowo odkrywać, część z nich dostrzega się dopiero po pewnym czasie. Wszystkie te detale składają się w jeden olbrzymi obraz kampanii napoleońskiej. Czy tym właśnie jest idealna grafika statystyczna? Czy chodzi o zaprezentowanie całej złożoności opisywanego zjawiska, wszystkiego, co jest w nim ważne, w formie jednego, wielowarstwowego obrazu? Z pewnością jest to świetny przykład czytelnej, estetycznej i bogatej w informacje wizualizacji.
Eksploracji danych nigdy dość
Wiek XX przyniósł, obok wielu innych odkryć w nauce, prawdziwy rozkwit grafiki statystycznej. Powstały czasopisma naukowe traktujące o tej dziedzinie, takie jak “Journal of Computational and Graphical Statistics”. Artykuły o wizualizacji danych można nawet znaleźć w wysoko cenionym przez statystyków periodyku “Journal of the American Statistical Association” i w wielu innych czasopismach. Prezentowaniem danych zajmują się statystycy, matematycy, lekarze, chemicy, fizycy, ekonomiści, dziennikarze, studenci i uczniowie i wiele innych grup.
Nowe sposoby pozyskiwania danych, nowe typy danych, nowe problemy badawcze dostarczają nowych wyzwań dotyczących prezentacji danych. Rosnąca ilość zbieranych danych umożliwia przedstawienie coraz to bardziej złożonych informacji o badanym zjawisku. Zamiast pokazywać średni/typowy wzrost człowieka, możemy opisywać rozkład wzrostu różnych osób. Prezentując predykcję, możemy zilustrować również jej szacowany błąd.
Prowadzi to do bardzo ciekawego wynalazku, który w prosty sposób pozwala na przedstawienie dla danego zjawiska więcej niż tylko średniej. Wynalazkiem, o którym mowa, jest wykres pudełko z wąsami, zwany też wykresem pudełkowym lub wykresem skrzynkowym (z ang. boxplot). Za projektanta tego typu wykresów i pierwszego człowieka, który je wykorzystywał, uznaje się Johna Tukeya (1915–2000).
John Tukey, podobnie jak bohaterowie poprzednich opowieści, miał bogaty i ciekawy życiorys. Studenci statystyki matematycznej znają go jako jednego z twórców testów statystycznych do porównywania średnich dla jednokierunkowej analizy wariancji czy metody estymacji jackknife. Tukey jest również znany informatykom, chociażby jako twórca terminu bit, który wprowadził jako skrót od binary digit. Osoby zajmujące się przetwarzaniem sygnałów mogą znać to nazwisko z uwagi na jego wkład w opracowanie algorytmu szybkiej transformaty Fouriera. Dla osób zajmujących się statystyczną prezentacją danych Tukey jest orędownikiem eksploracyjnej, opartej na wykresach i wizualizacjach, analizy danych.
Pierwszy wykres pudełkowy przedstawił w swojej książce Exploratory Data Analysis, opublikowanej w 1977 roku, a więc gdy autor miał już 62 lata. To interesująca pozycja, w której znajdziemy na przykład rady, jak używać pióra, by zwiększyć kontrast na ręcznie rysowanym wykresie.
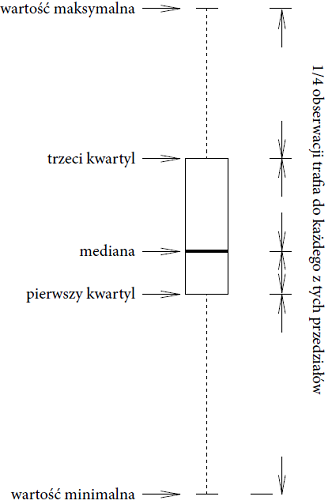 Rysunek 21: Przykładowy wykres pudełkowy. Przedstawia tak zwane pięć liczb Tukeya, czyli brzegi przedziałów dzielących zakres zmienności na cztery równoliczne części. Daje to wyobrażenie zarówno o zakresie zmienności (minimum/maksimum), najczęstszym zakresie zmienności (kwartyle dolny i górny) i medianie, czyli wartości środkowej. Źródło: opracowanie własne
Rysunek 21: Przykładowy wykres pudełkowy. Przedstawia tak zwane pięć liczb Tukeya, czyli brzegi przedziałów dzielących zakres zmienności na cztery równoliczne części. Daje to wyobrażenie zarówno o zakresie zmienności (minimum/maksimum), najczęstszym zakresie zmienności (kwartyle dolny i górny) i medianie, czyli wartości środkowej. Źródło: opracowanie własne
Jak ważnym odkryciem jest wykres pudełkowy? W eksploracyjnej analizie ma znaczenie kolosalne. Fantastycznie nadaje się do analizy typowych jednomodalnych zmiennych ilościowych, pozwala na odczytanie i porównanie dla kilku grup takich cech jak wartość centralna rozkładu (mediana zaznaczona jest kreską wewnątrz pudełka), typowy rozrzut (szerokość pudełka to przedział pokrywający połowę obserwacji), brak symetrii (czy mediana jest w środku pudełka), identyfikuje potencjalne wartości odstające (punktami zaznaczone są obserwacje odległe od najbliższego kwartyla o więcej niż półtora rozstępu międzykwartylowego) i typowy zakres przyjmowanych wartości (wąsy). I to wszystko na jednym wykresie! Co więcej, jeżeli chcemy porównać rozkład pewnej cechy w grupach, to umieszczone obok siebie wykresy pudełkowe dla poszczególnych grup łatwo umożliwiają natychmiastowe zauważenie różnic w wartościach typowych, zakresie zmienności czy skośności zmiennej dla poszczególnych grup.
Co ciekawe, wykres pudełkowy natychmiast doczekał się najróżniejszych modyfikacji pozwalających na prezentację większej liczby informacji o próbie pomiarowej (wykresy skrzypcowe i ich odmiany przedstawiające cały rozkład) lub tych samych danych w bardziej skondensowanej postaci (np. modyfikacja zaproponowana przez Edwarda Tuftego). Okazuje się jednak, że pięć charakterystyk rozkładu prezentowanych przez wykres pudełkowy z użyciem takich symboli, jakie zaproponował Tukey (a więc pudełka i wąsów), świetnie wpasowuje się w możliwości percepcyjne nieuzbrojonego oka. Większa ilość informacji zakłóca odczytanie tego, co najważniejsze, a minimalistyczne wersje mają zbyt mało elementów, by “zawiesić” na nich oko [Hadley Wickham and Lisa Stryjewski. 40 years of boxplots, 2011]
John Tukey był znany ze swojej niechęci do wykresów kołowych, mawiał, że nie istnieją takie dane, które można pokazać na wykresie kołowym, a których nie można pokazać lepiej na innego rodzaju wykresie. Był też orędownikiem wizualizacji danych jako podstawowej techniki eksploracji danych. Uważał również, że zbyt duży nacisk w pracy badacza kładziony jest na testowanie hipotez (analizę konfirmacyjną), a za mały na poznanie i oswojenie danych (analizę eksploracyjną). Jego myśl: Wielka jest wartość wykresu, który pozwala nam odkryć coś, czego się nie spodziewaliśmy, jest jednym z pięciu cytatów rozpoczynających ten zbiór esejów.
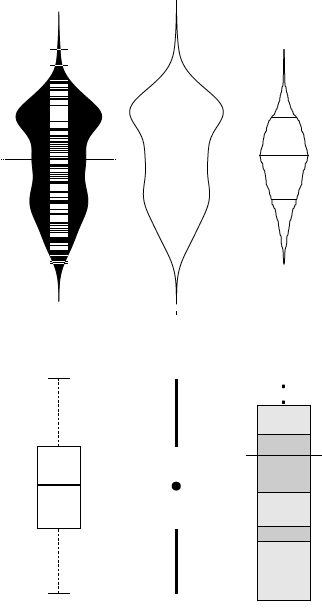 Rysunek 22: Rozmaite modyfikacje wykresu pudełkowego. Od lewej:
Wykres fasolkowy przedstawiający jądrową ocenę gęstości, poszczególne obserwacje i ich średnią (ang. bean plot), wykres skrzypcowy prezentujący jądrową ocenę gęstości (ang. violin plot), wykres percentylowy pokazujący percentyle (ang. percentile plot), wykres pudełkowy, minimalistyczna wersja wykresu pudełkowego opracowana przez Edwarda Tuftego, wykres natężeniowy HDR prezentujący obszary o wysokim zagęszczeniu obserwacji (ang. highest density regions). Źródło: opracowanie własne
Rysunek 22: Rozmaite modyfikacje wykresu pudełkowego. Od lewej:
Wykres fasolkowy przedstawiający jądrową ocenę gęstości, poszczególne obserwacje i ich średnią (ang. bean plot), wykres skrzypcowy prezentujący jądrową ocenę gęstości (ang. violin plot), wykres percentylowy pokazujący percentyle (ang. percentile plot), wykres pudełkowy, minimalistyczna wersja wykresu pudełkowego opracowana przez Edwarda Tuftego, wykres natężeniowy HDR prezentujący obszary o wysokim zagęszczeniu obserwacji (ang. highest density regions). Źródło: opracowanie własne
John Tukey jest również pomysłodawcą wykresu łodyga i liście (ang. stem and leaf), który przedstawia rozkład cechy w sposób podobny do histogramu, ale pozwalający na dokładne odczytanie każdej wartości. Ten sposób prezentacji danych jest obecnie często używany do przedstawiania rozkładów jazdy.
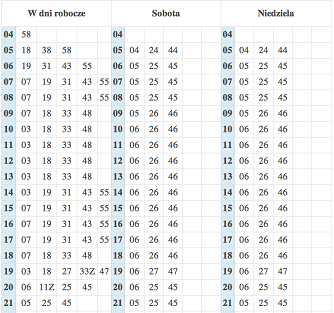 Rysunek 23: Rozkład jazdy wrocławskiego tramwaju 10. Źródło: strona internetowa MPK we Wrocławiu
Rysunek 23: Rozkład jazdy wrocławskiego tramwaju 10. Źródło: strona internetowa MPK we Wrocławiu
Statystyka pozwala na opisanie świata, ale to grafika statystyczna pomaga pojąć jego sens
W historii grafiki statystycznej zapisał się również szwagier Johna Tukeya statystyk Frank Anscombe (1918–2001). W 1973 roku skonstruował i przedstawił cztery zbiory danych nazywane dziś kwartetem Anscombe'a [Anscombe Frank. Graphs in statistical analysis. The American Statistician, 1973] W tamtych czasach badacze byli zachłyśnięci liniowymi zależnościami i możliwością użycia regresji liniowej do analizy danych i opisu zjawisk. Wydawało się, że wszędzie można zastosować to cudowne narzędzie i otrzymać krótki, zwięzły opis charakteru zależności pomiędzy dwiema zmiennymi.
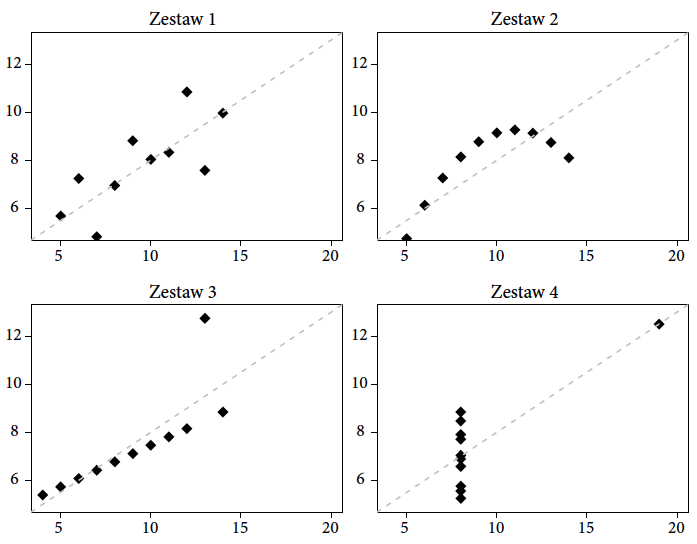
Anscombe przygotował cztery zestawy danych tak dobrane, by podstawowe statystyki liczbowe były dla nich identyczne. W każdym z tych czterech zbiorów danych mamy te same średnie, wariancje, współczynniki korelacji, regresji liniowej i wartości testów istotności dla współczynników w modelach liniowej regresji. Z punktu widzenia regresji liniowej te cztery zbiory danych są nierozróżnialne i w każdym z tych czterech przypadków mamy do czynienia z taką samą zależnością pomiędzy parą zmiennych.
Jednak proste przedstawienie graficzne tych czterech zestawów danych ilustruje oczywiste różnice pomiędzy nimi. Jest to wspaniały przykład wartości wizualizacji danych, która czasem potrafi opowiedzieć o danych więcej niż nawet zaawansowany model statystyczny.
Rysunek 24: Kwartet Anscombe'a. Średnia zmiennej przedstawionej na osi poziomej w każdym zestawie danych wynosi 9. Wariancja tej zmiennej w każdym zestawie danych wynosi 11. Średnie zmiennej pokazanej na osi pionowej w każdym z zestawów danych wynoszą 7,5, a ich wariancje są równe 4,12. Dla każdego z tych czterech zbiorów danych korelacje zmiennych na obu osiach wynoszą 0,816, a z punktu widzenia liniowych zależności wszystkie te dane najlepiej opisuje ten sam model regresji liniowej y=3+x/2. Źródło: opracowanie na bazie danych z~R
Wizualizacja danych to przecięcie sztuki, statystyki i projektu
John Tukey pojawia się też w życiorysie innej wielkiej postaci w dziedzinie graficznej analizy statystycznej – Edwarda Tuftego (statystyk, politolog, informatyk, rzeźbiarz 1942–). Edward Tufte pracował w Princeton jako statystyk. W 1975 roku prowadził zajęcia ze statystyki dla dziennikarzy. Ze względu na zainteresowania słuchaczy zajęcia te były poświęcone eksploracji danych oraz technikom prezentowania danych.
Ta tematyka wciągnęła Tuftego na tyle, że z Johnem Tukeyem zaczął prowadzić seminarium poświęcone grafice statystycznej. W 1982 roku opublikował książkę Visual Display. Jako że żaden wydawca nie chciał opublikować tekstu o takiej tematyce, Tufte wziął kredyt pod zastaw własnego domu, aby móc ją wydać. Książka okazała się wielkim sukcesem, podobnie jak jego kolejne dzieła: Envisioning Information, Visual Explanations oraz Beautiful Evidence
Tufte jest najbardziej znany ze swojego minimalistycznego podejścia do grafiki statystycznej. Wiele o jego filozofii prezentowania danych można znaleźć na stronie internetowej www.edwardtufte.com
Zdaniem Tuftego idealna prezentacja danych powinna mieć maksymalny współczynnik data-ink ratio, czyli możliwie mało zużytego tuszu na jednostkę informacji. Jeżeli zakres danych/informacji, które chcemy pokazać, jest ustalony, maksymalizację tego współczynnika można uzyskać przez minimalizację liczby elementów graficznych użytych do prezentowania danych. Mniej znaczy więcej!
Kolejnym wyznacznikiem dobrej wizualizacji, zdaniem Tuftego, jest możliwie mały współczynnik lie factor. W swoich książkach Tufte prezentował przykłady wykresów, które zniekształcały obraz pokazywanych danych. Czy te zniekształcenia powstały przypadkiem, przy okazji niepotrzebnego upiększenia wykresu, czy też celowo, by zmienić percepcję niepożądanego faktu, za każdym razem wykresy takie są przedstawiane jako sztandarowe przykłady, jak nie tworzyć grafiki statystycznej. Tropienie takich wątpliwych dzieł to hobby wielu osób.
W Internecie można znaleźć wiele kolekcji wykresów zmieniających percepcję zależności pomiędzy danymi. Ciekawe zestawy znajdują się na stronach InfoVis czy, w przypadku polskojęzycznych źródeł, na stronach fundacji SmarterPoland.pl w kategorii Zły wykres.
http://www.infovis-wiki.net/index.php/
Kategoria Zły wykres na blogu SmarterPoland.pl http://bit.ly/171brvV
http://www.SmarterPoland.pl/
Tufte znany jest również z popularyzacji terminu chart junk (wykresy śmieciowe), opisującego wykresy bardziej rozpraszające niż informujące. Choć termin ten został ukuty lata temu, mam wrażenie, że prawdziwa powódź tego typu śmieciowych wykresów, mających ładnie wyglądać, ale nic nie pokazujących, dopiero się rozpoczyna.
W wypowiedziach Tuftego widać jego zamiłowanie do szczegółów i postrzegania roli grafiki statystycznej jako grafiki o charakterze czysto informacyjnym.
Ciekawym pomysłem Tuftego, świetnie ilustrującym jego minimalistyczne podejście, są wykresy zintegrowane z oblewającym je tekstem. Przykładem są “iskierki” (ang. sparkline), prezentujące zmienność w czasie określonej wartości na wykresie o wysokości równej wysokości linii tekstu.
Profil zmian indeksu WIG w roku 2013 przedstawiony w postaci iskierki wygląda następująco:  Nie potrzebujemy zajmować połowy strony na pokazanie tego profilu. Widać na nim zmienność indeksu WIG oraz wzrostowy trend zmian w ciągu roku zakończony gorsza końcówką w grudniu. Nie musimy szukać wzrokiem na stronie miejsca, gdzie ten wykres się znajduje. Iskierki są ciekawym pomysłem na umieszczenie wykresu tam, gdzie jest potrzebny, i tak, by nie zajmował więcej miejsca niż to niezbędne dla zrozumienia jego głównej treści.
Nie potrzebujemy zajmować połowy strony na pokazanie tego profilu. Widać na nim zmienność indeksu WIG oraz wzrostowy trend zmian w ciągu roku zakończony gorsza końcówką w grudniu. Nie musimy szukać wzrokiem na stronie miejsca, gdzie ten wykres się znajduje. Iskierki są ciekawym pomysłem na umieszczenie wykresu tam, gdzie jest potrzebny, i tak, by nie zajmował więcej miejsca niż to niezbędne dla zrozumienia jego głównej treści.
Podobna oszczędność środków cechuje inne prace Edwarda Tuftego. Jego zdaniem idealny wykres prezentuje możliwie dużo informacji łatwych do odczytania w możliwie krótkim czasie, zapisanych możliwie małą ilością tuszu oraz na małej przestrzeni.
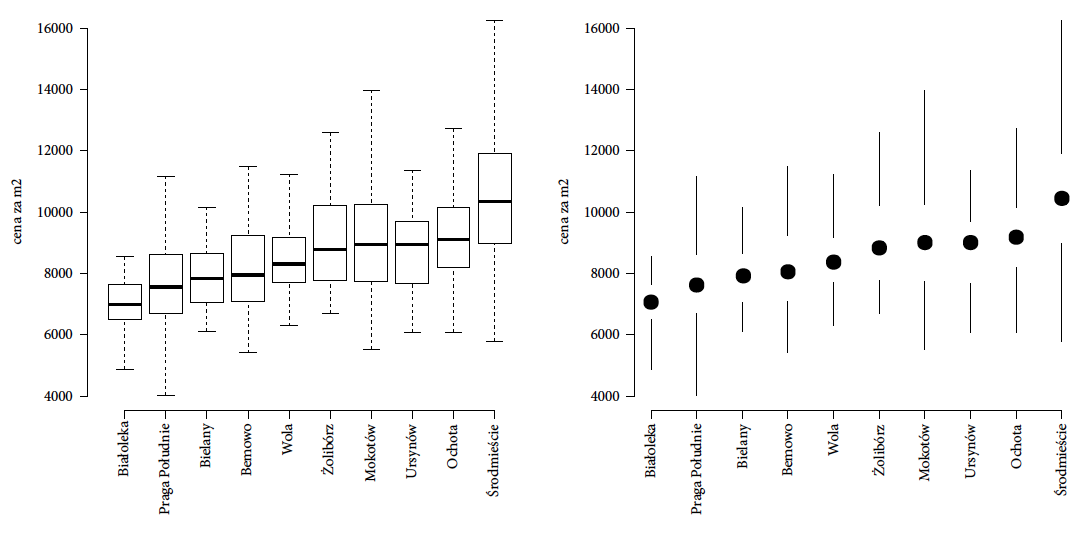 Rysunek 25: Rozkład cen metra kwadratowego w 2008 roku w różnych dzielnicach Warszawy. Po lewej stronie przedstawiony jest on za pomocą typowych wykresów pudełkowych, po prawej – przy użyciu ich minimalistycznej wersji zaproponowanej przez Edwarda Tuftego. Źródło: opracowanie własne
Rysunek 25: Rozkład cen metra kwadratowego w 2008 roku w różnych dzielnicach Warszawy. Po lewej stronie przedstawiony jest on za pomocą typowych wykresów pudełkowych, po prawej – przy użyciu ich minimalistycznej wersji zaproponowanej przez Edwarda Tuftego. Źródło: opracowanie własne
Edward Tufte jest również artystą tworzącym monumentalne rzeźby. To zderzenie sztuki i danych daje szerokie pole do ciekawych zapożyczeń. Często w argumentacji, dlaczego jeden wykres jest dobry, a drugi nie, Tufte odwołuje się do elegancji prezentacji. A ta elegancja jest wynikiem prostoty projektu oraz stopnia złożoności przedstawianej informacji.
Prace Edwarda Tuftego są przykładem tego, jak bardzo statystyczna prezentacja danych może zyskać inspirując się sztuką. Ale stymulacje płyną w obu kierunkach, również sztuka i artyści inspirują się danymi statystycznymi. Bardzo ciekawym przykładem takich motywacji są prace prof. Wiesława Łuczaja, dyrektora Instytutu Sztuk Pięknych Uniwersytetu Jana Kochanowskiego w Kielcach. Impulsem dla tworzonych przez niego dzieł sztuki są wyniki badań statystycznych Polaków. Zbiorcze raporty o stosunku do kary śmierci, bogactwa czy zdrowia stają się zarzewiem dzieł sztuki.
 ,,Obraz statystyczny – Szczęście 3'' z serii ,,Polak statystyczny'', akryl, płótno 200x200cm. Źródło: korespondencja z prof. Wiesławem Łuczajem
,,Obraz statystyczny – Szczęście 3'' z serii ,,Polak statystyczny'', akryl, płótno 200x200cm. Źródło: korespondencja z prof. Wiesławem Łuczajem
Wizualizacja danych to medium komunikacji
Edward Tufte jest też nauczycielem. Prezentuje i objaśnia reguły, którymi mogą podążać początkujący adepci sztuki wizualizacji danych. Ale nie tylko on w ostatnim wieku pracował nad zbiorami formuł pozwalających na opracowanie lepszych wykresów i schematów. Trzy, moim zdaniem najciekawsze, podejścia do tego tematu to te zaprezentowane przez francuskiego kartografa Jacques’a Bertina (1918–2010), amerykańskiego statystyka Williama Clevelanda oraz austriackiego socjologa Ottona Neuratha (1882–1945).
Podejście do statystycznej wizualizacji danych prezentowane przez Williama Clevelanda jest oparte na wynikach z jego badań nad percepcją. Cleveland przeprowadził serię eksperymentów w celu sprawdzenia, które składowe pomagają, a które utrudniają precyzyjne odczytanie z wykresu zależności pomiędzy przedstawianymi wielkościami. Pozwoliło mu to na zbudowanie hierarchii elementów graficznych, począwszy od tych pozwalających na zachowanie najlepszej dokładności (położenie wzdłuż wspólnej osi), przez elementy o ograniczonej możliwości przedstawiania wartości liczbowych (pola, objętości, kąty), po takie, które praktycznie zupełnie nie nadają się do prezentowania wielkości liczbowych na wykresie (kolory, kształty).
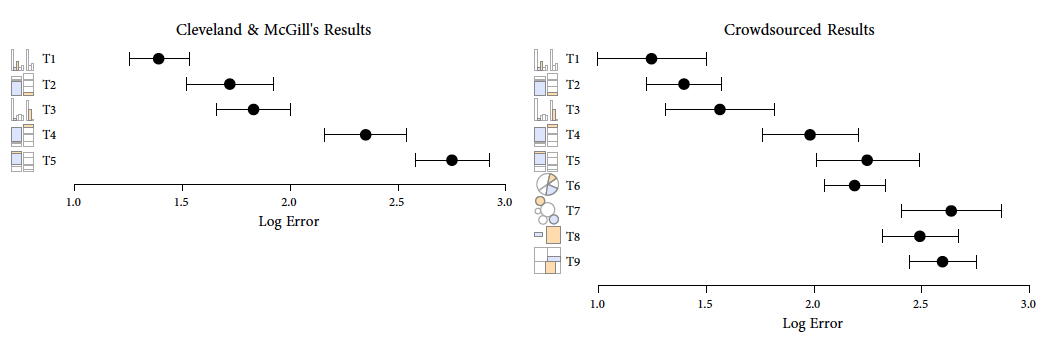 Rysunek 26: Średni względny błąd percepcji wielkości prezentowanych za pomocą różnych charakterystyk. T1 – wysokości sąsiednich pasków, T2 – pola prostokątów o wspólnej podstawie, T3 – wysokości odległych pasków, T4, T5 – pola prostokątów bez wspólnej podstawy, T6 – pola wycinków koła, T7 – pola kół, T8, T9 – pola niewyrównanych prostokątów. Wykres pochodzi z pracy Heera i Bostocka, 2010
Rysunek 26: Średni względny błąd percepcji wielkości prezentowanych za pomocą różnych charakterystyk. T1 – wysokości sąsiednich pasków, T2 – pola prostokątów o wspólnej podstawie, T3 – wysokości odległych pasków, T4, T5 – pola prostokątów bez wspólnej podstawy, T6 – pola wycinków koła, T7 – pola kół, T8, T9 – pola niewyrównanych prostokątów. Wykres pochodzi z pracy Heera i Bostocka, 2010
Jest to bardzo inżynierskie podejście, w którym wizualizację danych traktujemy jako medium komunikacji liczb i badamy, jaka jest efektywność tego kanału komunikacji. Efektywność można mierzyć czasem potrzebnym do odczytania obrazu lub dokładnością odczytu zakodowanych wartości. To podejście zakłada, że istnieje jeden sposób odczytania tej wiadomości, co pozwala na badanie, czy przesył był skuteczny: czy zakończył się sukcesem (wiadomość odczytana poprawnie, zgodnie z intencją nadawcy), czy porażką (wiadomość odczytana niepoprawnie).
Badania prowadzone przez Clevelanda były i wciąż są podejmowane przez innych badaczy. Ciekawą kontynuacją jest analiza przeprowadzona przez Jeffreya Heera i Michaela Bostocka [Jeffrey Heer and Michael Bostock. Crowdsourcing graphical perception: using mechanical turk to assess visualization design], wykorzystująca serwis Mechanical Turk firmy Amazon do przeprowadzenia testu percepcji na znacznie szerszą skalę. W zależności od rodzaju testu grupa ankietowanych liczyła od tysiąca do dwóch tysięcy osób. Tak duża próba pozwoliła na precyzyjną ocenę błędu percepcji różnych charakterystyk wykresu. Podobnie jak w badaniach Clevelanda okazało się, że najbardziej precyzyjnie odczytywane są długości pasków umieszczonych obok siebie i zaczynających się we wspólnym początku – pionowej osi.
Inaczej wygląda podejście prezentowane przez Jacques'a Bertina (1918–2010, francuski kartograf, geograf i teoretyk grafiki), opisane w jego dziele Semiologia grafiki, opublikowanym po raz pierwszy w 1967 roku. Semiologia to nauka zajmująca się badaniem funkcji znaku w procesie porozumiewania się. Znaki i symbole mają przypisane znaczenia, które mogą się różnić w zależności od odbiorcy. Oczekiwane jest więc, że różni odbiorcy odczytają znaki w odmienny sposób i jest to wpisane w proces komunikacji. Takiej różnorodnej interpretacji powinniśmy się wręcz spodziewać. Nie sposób też określić, która z interpretacji jest poprawna, a która nie, każda jest prawidłowa w określonym kontekście (np. kulturowym).
Przyjmując takie podejście, zamiast badać, czy przesył był “poprawny”, możemy się zastanowić, jak pewnego rodzaju kompozycje są odczytywane, i od początku projektowania wykresu uwzględnić charakterystykę odbiorcy.
Mało użyteczne są wykresy nieprzedstawiające żadnych informacji lub przedstawiające informacje, które trudno na nich odnaleźć. Wykres z tytułem Zmiana średnich wynagrodzeń może być mało użyteczny, jeżeli odbiorca nie potrafi odgadnąć, jaki element wykresu pokazuje średnie wynagrodzenia, czy jest to powierzchnia czegoś, czy długość, czy pozycja na skali. Jak pokażemy później, zdarzają się wykresy, dla których nie jest tak łatwo odczytać intencje autora wykresu dotyczącą charakterystyki przedstawiającej dane.
Użyteczność wykresu jest rozumiana jako łatwe odnalezienie informacji na wykresie (oczywiście dana informacja musi być na nim obecna) oraz łatwe odczytanie celu, w którym dana cecha (charakterystyka) kompozycji została użyta (czy np. jasny kolor na wykresie odpowiada wysokim, czy niskim wartościom) przy jednoczesnym poprawnym zastosowania reguły mapowania danej charakterystyki (czyli np. odpowiednie użycie koloru lub kierunku linii).
Aby ułatwić tworzenie użytecznych wykresów, Bertin systematycznie opisał różnego rodzaju konstrukcje i charakterystyki, uzasadniając, które nadają się do jakich funkcji.

Badania Bertina, kontynuowane między innymi przez Lelanda Wilkinsona [Leland Wilkinson.
The Grammar of Graphics, 1999], prowadzą do lepszego zrozumienia sposobu, w jaki nasz umysł postrzega i odczytuje wykres. W procesie tym istotną rolę pełni rodzaj pytania, na które nasz umysł stara się odpowiedzieć. Bertin pokazuje, jak użyteczność zastosowania różnych charakterystyk, takich na przykład jak kolor, kształt, wielkość czy tekstura, zależy od roli, jaką mają pełnić na wykresie.
Ta filozofia konstrukcji wykresu widoczna jest na przykład w pracy z narzędziami typu pakiet ggplot2[Hadley Wickham.
ggplot2: elegant graphics for data analysis, 2009], gdzie budowa wykresu jest związana głównie z opisem mapowania pomiędzy zmiennymi a elementami wykresu.
Rysunek 27: W kolumnach przedstawiono zadania analityczne zdefiniowane przez Jacques'a Bertina (wyróżnienie obiektów o wspólnych cechach, rozróżnienie obiektów o różnych cechach, przedstawienie cechy liczbowej/ilościowej, przedstawienie cechy jakościowej/uporządkowanej), w wierszach przedstawiono charakterystyki wykresu. W komórkach tabeli przedstawiono, jak zdaniem Bertina dana cecha pasuje do określonego zadania analitycznego. Znak + oznacza, że dana charakterystyka sprawdza się w realizacji danego zadania analitycznego, znak ? oznacza, że dana charakterystyka jest użyteczna w określonych sytuacjach. Przykładowo barwa jest dobrą charakterystyką do wyróżniania elementów lub pokazywania grup elementów, ale jest złym wyborem do prezentacji wartości ilościowych
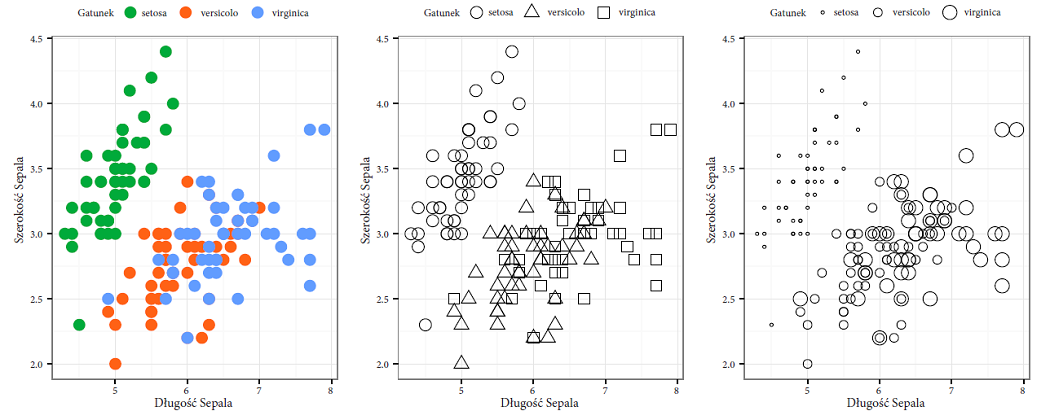 Rysunek 28: Użyteczność takich charakterystyk jak kolor, kształt i wielkość w funkcji wyróżnienia (ang. selective) lub grupowania (ang. associative). Łatwiej dostrzec grupy obiektów, gdy są zaznaczone kolorami. Rozróżnienie obiektów z grupy versicolor i virginica jest trudniejsze, jeżeli są one przedstawione za pomocą kształtów lub wielkości. Źródło: opracowanie własne
Rysunek 28: Użyteczność takich charakterystyk jak kolor, kształt i wielkość w funkcji wyróżnienia (ang. selective) lub grupowania (ang. associative). Łatwiej dostrzec grupy obiektów, gdy są zaznaczone kolorami. Rozróżnienie obiektów z grupy versicolor i virginica jest trudniejsze, jeżeli są one przedstawione za pomocą kształtów lub wielkości. Źródło: opracowanie własne
Barwy nie nadają się do przedstawiania zmiennych ilościowych, ponieważ nie istnieje uniwersalny klucz ich kolejności. Jednak kolor nie jest bezużyteczny, może pełnić ważną rolę w procesie grupowania lub wyróżniania/identyfikowania obiektów. Nasz umysł łatwo wyszuka grupy obiektów o tym samym kolorze. Do zadania grupowania podobnych obiektów barwa nadaje się lepiej niż, przykładowo, kształt.
Inne ciekawe podejście do grafiki statystycznej prezentował socjolog Otto Neurath, który uważał, że grafika statystyczna powinna pełnić rolę edukacyjną dla społeczeństwa. Aby to stało się możliwe, musi być zrozumiała i interesująca, łatwa do zapamiętania i precyzyjna. W tym celu Neurath w latach trzydziestych XX wieku opracował język ISOTYPE zaprojektowany do łatwego zrozumienia wykresów tak, by na ich podstawie możliwa była “edukacja wizualna” społeczeństwa.
Język ISOTYPE to zestaw symboli i reguł, wskazówek, jak prezentować graficznie informacje w sposób zrozumiały dla szerokiego odbiorcy. Zawiera listy precyzyjnie zaprojektowanych znaków/piktogramów o uniwersalnych znaczeniach oraz reguły czytelnego i dokładnego używania tych piktogramów w celu prezentowania informacji. Jedną z najbardziej charakterystycznych reguł jest zasada używania powtórzeń znaku do przedstawiania wielkości. Porównując dwie wartości, z których jedna jest o 50% większa od drugiej, na wykresie paskowym użylibyśmy dwóch pasków, z których jeden byłby o 50% dłuższy niż drugi. W pewnych sytuacjach wykorzystanie liczby powtórzeń pewnego piktogramu zamiast długości pozwala na czytelniejsze i ciekawsze zaprezentowanie określonej wartości.
Ten “język wizualny” został tak skonstruowany, by ułatwić zrozumienie danych liczbowych opisujących współczesny świat. Jedno z większych dzieł stworzonych z użyciem tego języka to Modern man in the making (1939)[Neurath Otto. Modern Man In The Making 1939], autorstwa Ottona Neuratha. Książka ta przestawia zbiór ciekawych statystyk dotyczących społeczeństwa, pokazujących, jak wyglądał ówczesny świat. Dzisiaj dzieła Ottona Neuratha są dostępne w domenie publicznej. Książkę “International Picture Language” można pobrać ze strony http://bit.ly/1J23Cs9 a książkę “Modern Man in the Making” ze strony http://bit.ly/207glBb Rysunek 31 pochodzi z tej drugiej i przedstawia wielkość różnych imperiów na przestrzeni dziejów.
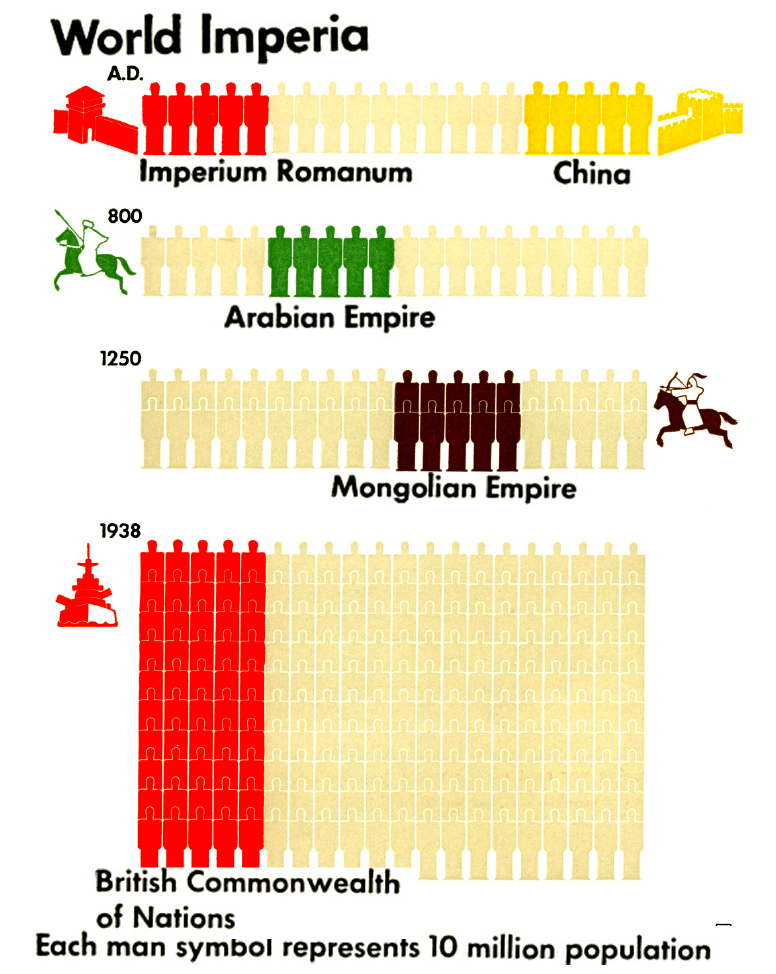 Rysunek 31: Światowe imperia w różnych okresach historii. Źródło: Modern Man in the Making, Otton Neurath
Rysunek 31: Światowe imperia w różnych okresach historii. Źródło: Modern Man in the Making, Otton Neurath
Więcej o języku ISOTYPE można przeczytać również we wpisie Młodzi XXL, Eurostat a problem nadwagi i otyłości autorstwa Magdy Małczyńskiej-Umedy przygotowanym dla fundacji SmarterPoland.pl.

“Młodzi XXL, Eurostat a problem nadwagi i otyłości” Magda Malczynska-Umeda dla fundacji SmarterPoland.pl http://bit.ly/YOBEYw
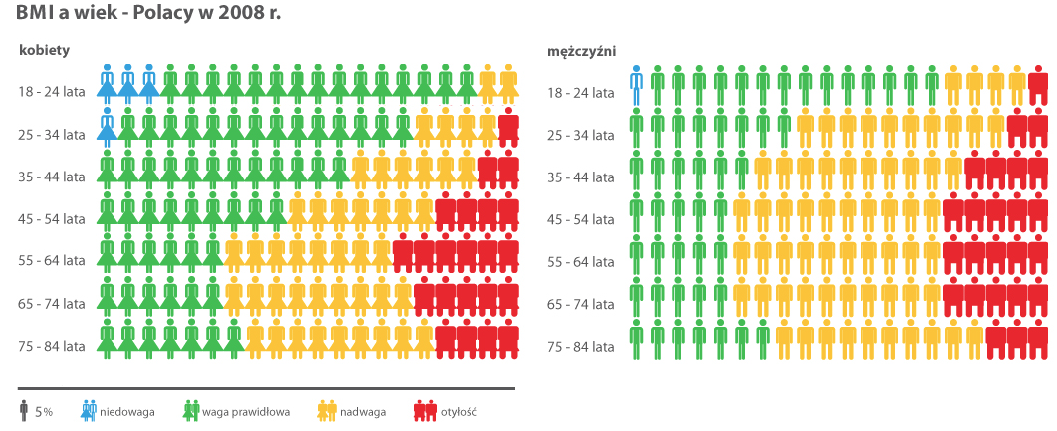 Rysunek 29: Udział osób z niedowagą lub nadwagą w różnych grupach wiekowych. Do prezentowania wielkości użyto powtarzających się symboli, zgodnie z regułami języka ISOTYPE. Użycie pogrubionych ikon w czerwonym kolorze do oznaczenia osób otyłych, może spowodować optyczne powiększenie udziału tej grupy. Źródło: wykres opracowała Magda Małczyńska-Umeda
Rysunek 29: Udział osób z niedowagą lub nadwagą w różnych grupach wiekowych. Do prezentowania wielkości użyto powtarzających się symboli, zgodnie z regułami języka ISOTYPE. Użycie pogrubionych ikon w czerwonym kolorze do oznaczenia osób otyłych, może spowodować optyczne powiększenie udziału tej grupy. Źródło: wykres opracowała Magda Małczyńska-Umeda
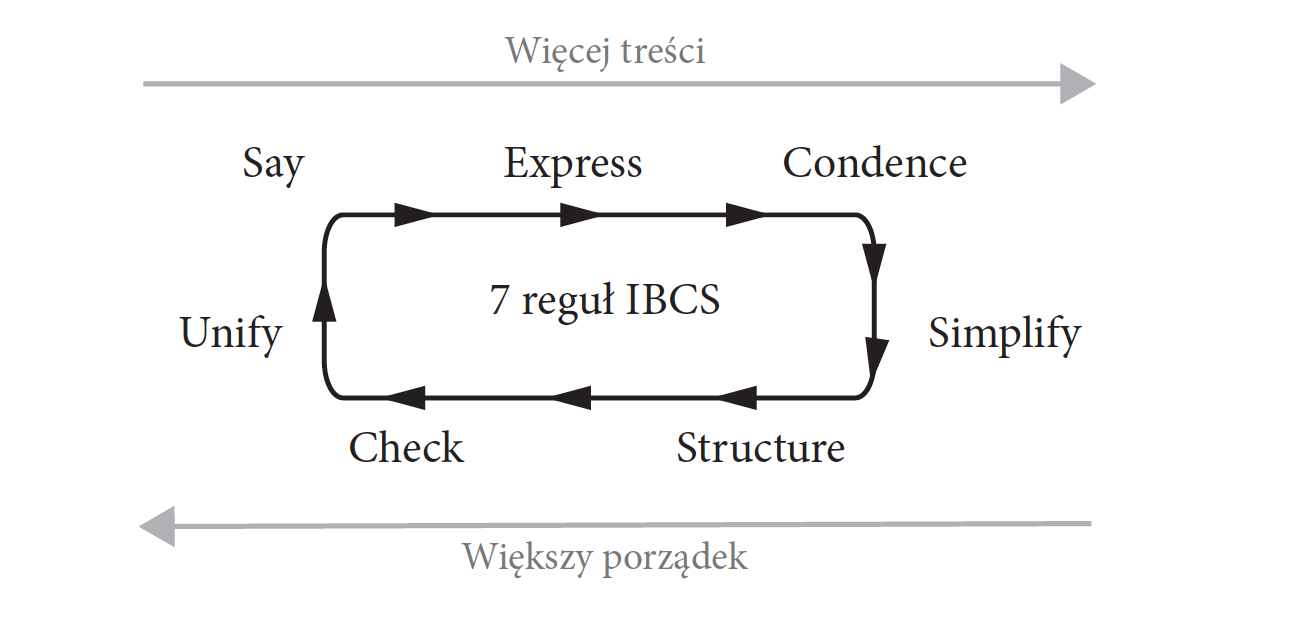
Reguły ISOTYPE zostały opracowane na potrzeby popularyzacji danych statystycznych szerokiej grupie odbiorców. Co jednak w sytuacji gdy komunikujemy się z wąską grupą specjalistów? W tej sytuacji często znajdują się analitycy lub kontrolerzy finansowi, którzy pracują ze zbiorami danych bogatymi w relacje i stoją przed wyzwaniem przedstawienia tych zależności przed partnerami biznesowymi lub zarządem. Mogą oni skorzystać z Międzynarodowych Standardów Komunikacji Biznesowej (ang. The International Business Communication Standards). Ten zbiór standardów został zainicjowany przez Rolfa Hicherta i Jürgena Faissta, obecnie rozwijany jest przez otwarte stowarzyszenie IBCS-A. Szczegółowy opis tych standardów można pobrać ze strony http://www.ibcs-a.org/ Składają się one ze zbioru wskazówek i rekomendacji, które są pogrupowane w siedem reguł udanej komunikacji. Pierwsze litery tych reguł układają się w słowo SUCCESS. Reguły te wraz z krótkim komentarzem, przedstawione są w tabeli 32.

Tabela 32:
Podstawowe siedem reguł IBCS. Dla każdej reguły, na stronie http://www.ibcs-a.org przedstawione są szczegółowe przykłady czego unikać, a co stosować
Rysunek 33:
Reguły SUCCESS można stosować w sposób iteracyjny. Część reguł służy wzbogaceniu wykresu lub raportu w dodatkowe informacje, a część związana jest z organizacją elementów by ułatwić ich odszukanie i odczytywanie. Źródło: opracowanie własne
Przykładowa rekomendacja dotycząca reguły Express (wybieraj odpowiednią formę dla prezentowanych danych) jest przedstawiona na rysunku 34. Stosowanie wykresów imitujących szybkościomierze do przedstawienia jednej liczby to klasyczny przerost formy nad treścią. Zazwyczaj można przedstawić więcej informacji w bardziej czytelny sposób.
Przykładowa rekomendacja dotycząca reguły Unify (stosuj jednolite schematy oznaczania i wyróżniania) jest przedstawiona na rysunku 34. Łatwiej odczytywać dane z wykresów, jeżeli mają one te same jednostki. Jeżeli jest to niemożliwe, lub spowodowałoby, że wykres stałby się mało czytelny, wtedy warto zaznaczyć jak jednostki na jednym wykresie mają się do jednostek na innych wykresach.
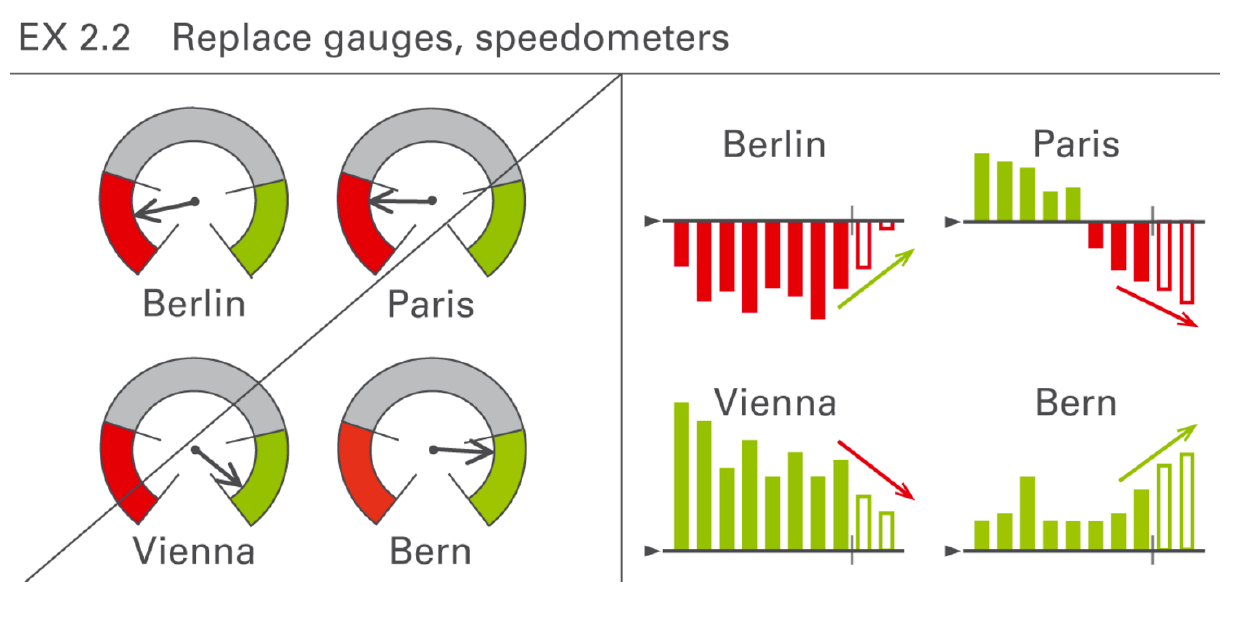
Rysunek 34: Ilustracja jednej z reguł IBCS. Szybkościomierze przedstawiają jedną liczbę w dosyć barokowy sposób. Można więcej informacji czytelniej przedstawić za pomocą wykresów słupkowych. Źródło: International Business Communication Standards, http://www.ibcs-a.org/

Rysunek 35: Ilustracja jednej z reguł IBCS. Aby ułatwić porównywanie wartości pomiędzy wykresami warto zadbać o identyczność jednostek na wykresach. Jeżeli jest to niemożliwe to warto zaznaczyć, czym te jednostki się różnią. Źródło: International Business Communication Standards, http://www.ibcs-a.org/
Polacy nie gęsi
Prawdopodobnie pierwsza polskojęzyczna książka poświęcona wizualizacji danych to “Graficzne metody w statystyce planowaniu i ewidencji” Ł. Byzowa. Została ona wydana w języku rosyjskim w roku 1940, a na język polski została przetłumaczona w roku 1951. Rok 1940 to dwa lata przed urodzeniem się Edwarda Tufte i 37 lat przed tym jak John Tukey napisał “Exploratory Data Analysis’’.
W tej książce przedstawione są zarówno interesujące wykresy jak i techniki ich przygotowywania. Na dzień dzisiejszy te techniki mogą uchodzić za prymitywne (np. zastosowanie maszyny do pisania do przygotowania wykresu, patrz rysunek 36) ale komentarze dotyczące interpretacji i tworzenia wykresów są ponad czasowe.
Byzow opisuje procesy myślowe, które potrzebne są do odczytania wykresu lub do opracowania wykresu. Są to co prawda komentarze z czasów, gdy wykresy nie były tak wszechobecne, ale wciąż można dzięki nim można spojrzeć na konstrukcję wykresów ze świeżej perspektywy. Byzow przedstawia wykres jako interpretację rzeczywistości. Zaznacza, że wykres nie jest wiernym odwzorowaniem rzeczywistości – nie jest zdjęciem – ale jest komentarzem rzeczywistości z naniesionymi przez autora wykresu akcentami.

Rysunek 36: Przykładowy diagram sporządzony na maszynie do pisania. Źródło: Ł. Byzow
Historia na wykresie jest zakodowana przez elementy graficzne wybrane przez autora. Czytelnik musi te elementy zidentyfikować i odkodować. Przez to początkowo odczytywanie wykresu wymaga większego wysiłku niż prosty komunikat słowny. Przy bardziej złożonych komunikatach ten początkowy “narzut” się zwraca.
Pierwszą książką o wizualizacji danych napisaną w oryginale w języku polskim jest “Jak sporządzać wykresy statystyczne” opracowana w roku 1957 przez Ignacego Osipowa, pracownika Głównego Urzędu Statystycznego. Oczywiście wykresy umieszczano we wcześniejszych publikacjach, ale ta książka jako pierwsza opisywała jak je poprawnie tworzyć. Ignacy Osipow przestawiał wykresy opisujące stan państwa, ale też podkreślał, że rola wykresów wychodzi dalece poza popularyzację danych statystycznych. Zauważał, że wykresy mogą ułatwiać naukową analizę danych oraz komunikację odkrytych zależności.
Od tego czasu opublikowano w języku polskim wiele książek o wizualizacji danych. Można je z grubsza podzielić na kilka grup. Część z nich to instruktaże, jak krok po kroku wykonać wykres w Excelu lub innym narzędziu. Część z nich skierowana jest do projektantów graficznych, pracujących najczęściej przy infografikach. Pojawiły się też publikacje naukowe analizujące wykresy z punktu widzenia retoryki i skuteczności przekonywania odbiorcy do określonych tez. Są też publikacje związane z zastosowaniami wykresów w określonym obszarze zastosowań.
Weźmy za przykład kartografię. Ostatnio Główny Urząd Statystyczny opublikował na licencji Creative Commons podręcznik “Graficzna prezentacja danych statystycznych. Wykresy, mapy, GIS”. Podręcznik powstał w ramach współpracy polsko-gruzińskiej i GUS dzieli się w nim doświadczeniami w prezentowaniu danych.
Cały podręcznik jest dostępny w postaci elektronicznej pod adresem http://bit.ly/1Oy5qsI.Tematy i przykłady krążą wokół danych prezentowanych przez GUS jest więc sporo klasycznych rozwiązań. Niektóre prezentacje są bardzo pomysłowe i ciekawe. Dwie przykładowe są przedstawione na rysunku 38.
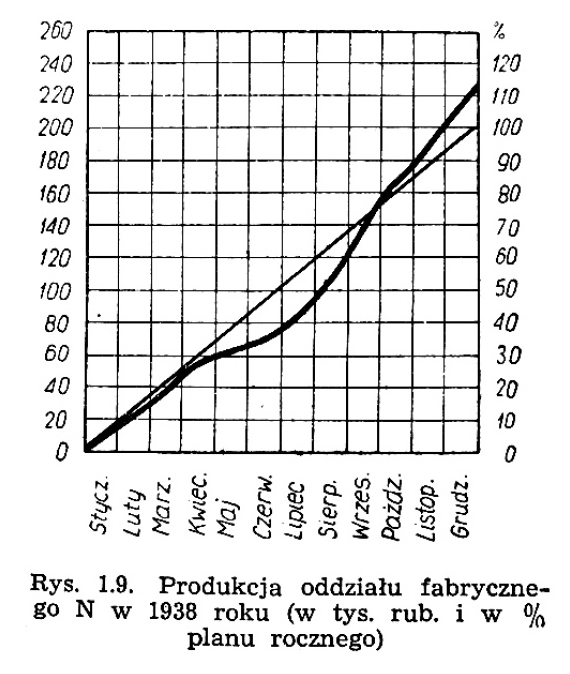 Rysunek 37: Wykres przedstawiający produkcję w fabryce w odniesieniu do planu. Dwie krzywe składają się na ciekawą historię o opóźnieniach w drugim kwartale i wynikiem ponad normę pod koniec roku. Źródło: Ł. Byzow
Rysunek 37: Wykres przedstawiający produkcję w fabryce w odniesieniu do planu. Dwie krzywe składają się na ciekawą historię o opóźnieniach w drugim kwartale i wynikiem ponad normę pod koniec roku. Źródło: Ł. Byzow
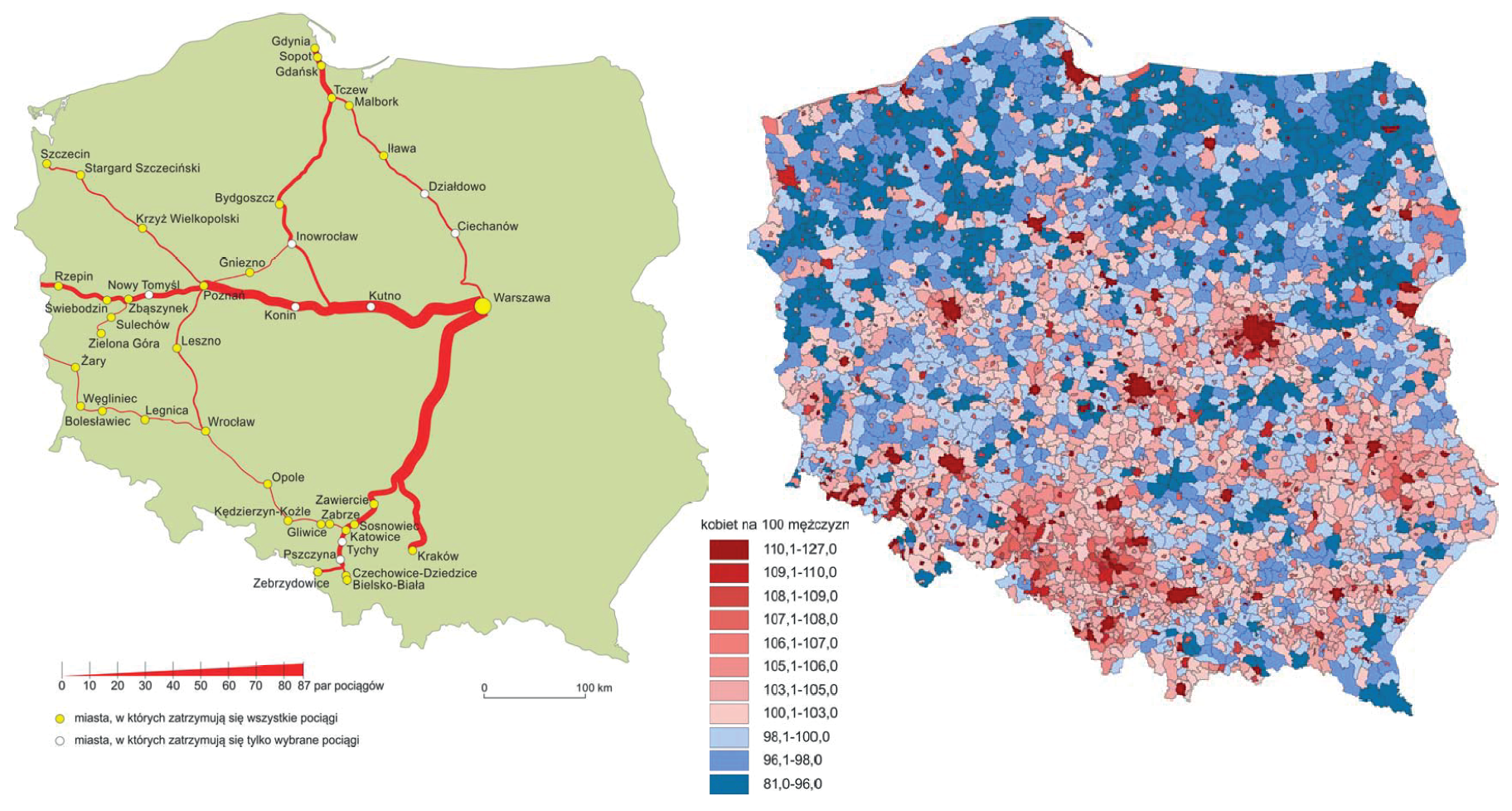 Rysunek 38: Kartodiagram liniowo wstęgowy, połącznia kolejowe InterCity i EuroCity nie są równomiernie rozłożone.
Kartogram liczby kobiet przypadających na 100 mężczyzn z podziałem na gminy.
Źródło: Graficzna prezentacja danych statystycznych. GUS
Rysunek 38: Kartodiagram liniowo wstęgowy, połącznia kolejowe InterCity i EuroCity nie są równomiernie rozłożone.
Kartogram liczby kobiet przypadających na 100 mężczyzn z podziałem na gminy.
Źródło: Graficzna prezentacja danych statystycznych. GUS
Inną publikacją w podobnej tematyce jest “Atlas Metod Kartograficznych” wykonany przez zespół prof. Jacka Pasławskiego. Atlas ten jest dostępny na stronie http://www.educarto.pl/ i przedstawia różne techniki nanoszenia na mapy danych, wartości lub zależności[NA] Jest poprzedzony bardzo ciekawym wstępem historycznym dotyczącym izolinii, kartogramów i innych typów grafik. Na rysunku 39 przedstawiamy przykładową mapę kropkową wielowagową dla województwa mazowieckiego.
Do Atlasu dołączona jest aplikacja www, dostępna na stronie http://bit.ly/1QCRfpo Ta aplikacja pozwala na oglądanie kartogramów i kartodriagramów przy różnych ustawieniach dotyczących skalowania, skal i innych parametrów.
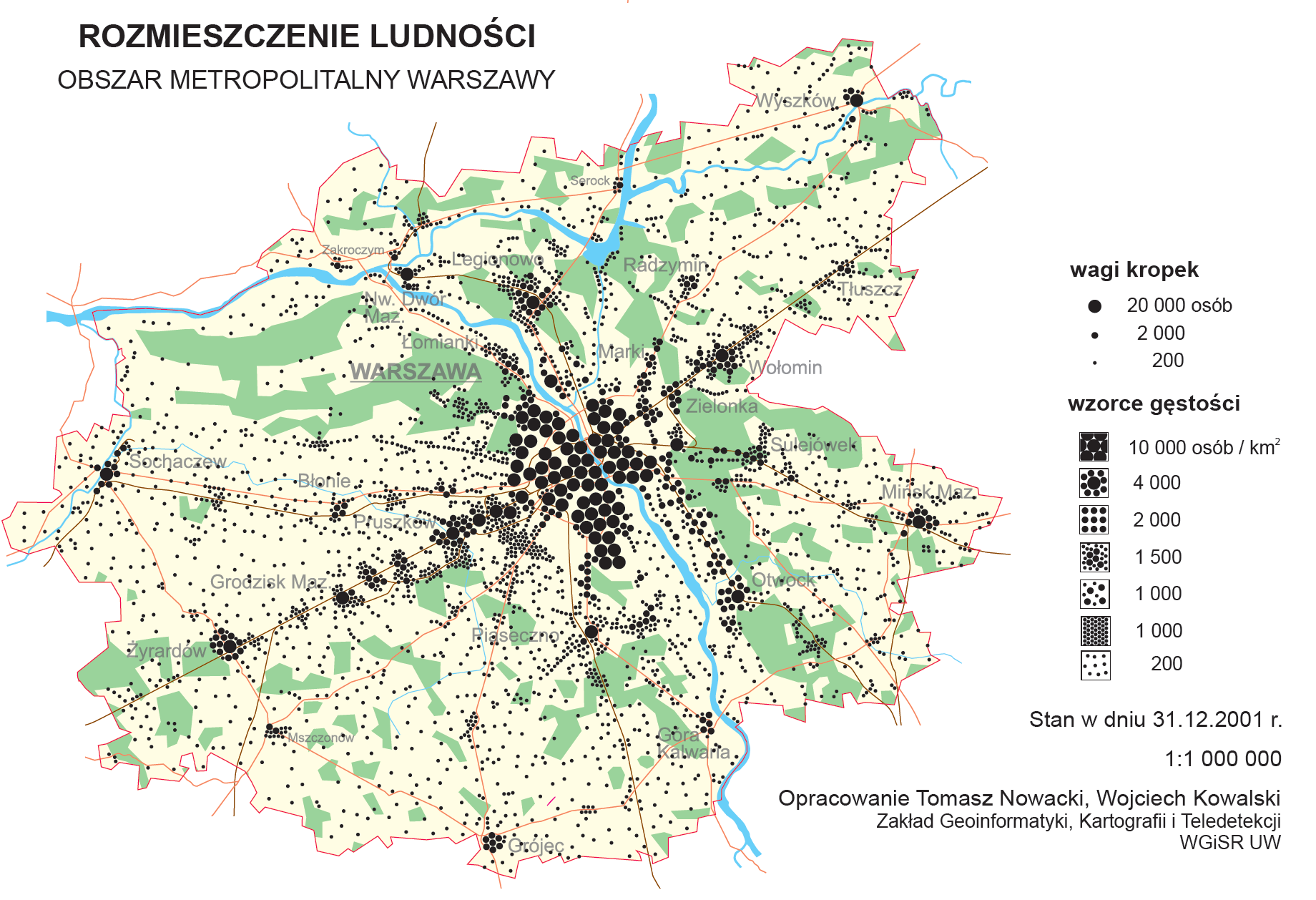 Rysunek 39: Rozmieszczenie ludności w okolicach Warszawy. Źródło: Atlas Metod Kartograficznych, za zgodą autorów. http://www.educarto.pl/
Rysunek 39: Rozmieszczenie ludności w okolicach Warszawy. Źródło: Atlas Metod Kartograficznych, za zgodą autorów. http://www.educarto.pl/
Aby pokazać informację, należy ją najpierw zrozumieć
Zasłużonych osób, przełomowych zdarzeń i świetnych pomysłów jest oczywiście w historii grafiki statystycznej znacznie więcej niż zaprezentowałem. Historia wizualizacji danych tworzona jest na naszych oczach i nie widać jej końca. Codziennie powstaje wiele nowych wykresów, pojawiają się różne dane i różne sposoby ich prezentowania.
Moja przygoda z grafiką statystyczną rozpoczęła się od książek Tuftego, które zachwyciły mnie prostotą i elegancją przekazu informacji. Ale jako osoba zajmująca się statystyką matematyczną musiałem ukrywać tę sympatię do wizualizacji danych. Pracowałem wtedy w środowisku ponad wszystko ceniącym twierdzenia. A jeżeli już nie twierdzenia, to przynajmniej tabele liczb. Wizualizacja tabel liczb tak, by inni łatwiej mogli te liczby zrozumieć, była przejawem słabości intelektualnej osoby potrzebującej udogodnienia w postaci wykresu. Szokiem – używam tego słowa bez zbędnej przesady – było dla mnie odkrycie, że takie osobistości jak John Tukey czy Frank Harrell uznawały wizualizację danych za podstawowe narzędzie statystyka. Z pasją neofity zacząłem szukać innych przykładów, by odkryć, jak wielką rolę wizualizacja danych odgrywała przy wielkich odkryciach. Odpowiednio przedstawiając dane, możemy je lepiej zrozumieć, a lepiej je rozumiejąc, możemy je jeszcze lepiej pokazać. To zamknięty cykl. Jeżeli chcemy zaprezentować jakieś zjawisko, musimy je rozumieć, aby przedstawić to co istotne. Ale żeby ułatwić sobie zrozumienie, warto to zjawisko pokazać.
Jako ostatni przykład zdecydowałem się zatem pokazać wizualizację informacji o znaczeniu kluczowym dla XXI wieku. Koniec XX wieku to okres wielkiego wyścigu w kosmos. Początek XXI wieku to wielki biotechnologiczny wyścig ku zrozumieniu i przejęciu kontroli nad wieloma biologicznymi procesami na poziomie genetycznym. Rewolucja ta była możliwa dzięki odkryciu struktury DNA i właśnie z tym odkryciem związany jest niesamowicie ciekawy przykład, ilustrujący siłę wzmocnienia pętli odkrycie -– prezentowanie danych z odkrycia.
Chodzi mi o historię odkrycia struktury DNA. Odkrywcy nie mogli zobaczyć tej struktury, widzieli tylko zachowanie się prążków interferencyjnych na zdjęciach rentgenowskich. James Watson i Francis Crick starali się sobie wyobrazić, jak ta struktura może wyglądać, ale jej nie widzieli. Pisząc swój artykuł do “Nature”[James Watson i Francis Crick. Molecular structure of nucleic acids. Nature, 1953], chcieli oczywiście pokazać budowę DNA możliwie najwierniej na schemacie. Ale jak to zrobić, nigdy jej nie wdziawszy?
Francis Crick naszkicował żonie swoje wyobrażenie, jak ta struktura może wyglądać. Tak się złożyło, że jego żona, Odile Crick, była projektantką. Wykorzystując umiejętności projektanta w celu czytelnego przedstawienia informacji, zamieniła szkic męża w rysunek, który został opublikowany w “Nature” razem z artykułem opisującym budowę DNA. Czytelnicy byli zafascynowani pięknem pokazanej struktury. Pięknem, które powstało ze starannego projektu, czytelnie przedstawiającego tak pożądaną informację. Projekt pokazywał to, co istotne w strukturze DNA, czyli podwójną helisę usztywnioną wiązaniami pomiędzy nukleotydami, ale bez zbędnych szczegółów, które zakłóciłyby przekaz.
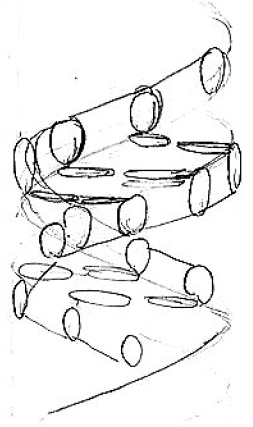 Rysunek 30: Szkic Francisa Cricka pokazujący strukturę DNA. Źródło: Wellcome Library, licencja Creative Commons Attribution
Rysunek 30: Szkic Francisa Cricka pokazujący strukturę DNA. Źródło: Wellcome Library, licencja Creative Commons Attribution
Wielu badaczy mówiło później, że piękno prostoty tej struktury działało jak środek hipnotyzujący. Uwiarygodniało całe odkrycie. Jest to wspaniały przykład na to, że właściwa prezentacja danych ma kluczowe znaczenie.
Zauważmy, że wiele z powyższych nazwisk – da Vinci, Snow, Priestley – znamy jako nazwiska chemików, fizyków, ekonomistów, historyków, architektów, odkrywców. Jest to też wskazówka, która pokazuje, że potrzeba prezentowania danych często idzie w parze z odkryciami, a odkrycia są źródłem nowych sposobów prezentowania danych.
Historia wizualizacji danych to historia wielkich odkryć ludzkości. Potrzebne były nowe środki i techniki prezentowania coraz to bardziej złożonej informacji tak, by nasz mózg, przez ewolucję przystosowany do przetrwania na sawannie, potrafił tę nową, skomplikowaną informację ogarnąć i przyswoić.
Dla mnie grafika statystyczna to medium czytelnie przedstawiające informacje zawarte w danych, czyli czasami nowe idee i odkrycia, a czasami po prostu rzetelną wiedzę na określony temat.
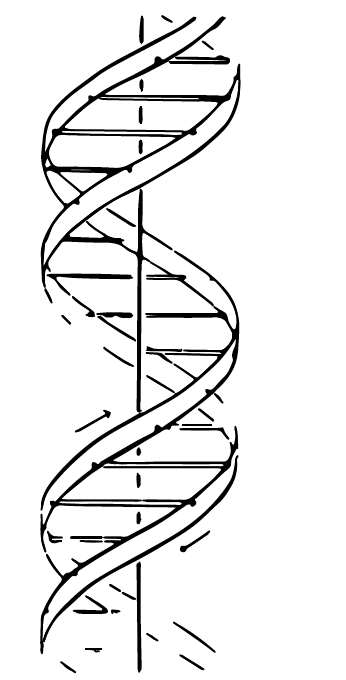 Rysunek 31: Schemat DNA opracowany i naszkicowany przez Odile Crick. Źródło: własna wektoryzacja na bazie szkicu Odile Crick
Rysunek 31: Schemat DNA opracowany i naszkicowany przez Odile Crick. Źródło: własna wektoryzacja na bazie szkicu Odile Crick