
Praca z danymi to najczęściej wielokrotna iteracja pętli hipoteza – analizy – wnioskowanie. Wyniki z każdej iteracji pomagają sprecyzować pytanie, rozbudować model o nowe czynniki, poprawić sposób prezentacji wniosków. Każda iteracja zwiększa nasze zrozumienie zjawiska, co pozwala na coraz to lepszą jego analizę i prezentację.
Prezentując wyniki, czy to w postaci graficznej, czy poprzez tabelę z liczbami, zazwyczaj pokazuje się jedynie końcowe rozwiązanie. Ma to oczywiście sens, ponieważ to końcowe rozwiązanie jest z reguły najlepszą odpowiedzią na rozważane pytanie. Jednak w nauce modelowania i prezentacji danych często bardzo pomocne jest nie tylko zobaczenie końcowego wyniku, ale również całej ścieżki prowadzącej do tego wyniku. Przyglądając się całej ścieżce rozumowania, można lepiej zrozumieć intencje oraz wybory, które prowadziły do końcowego rozwiązania.
Zazwyczaj, gdy opowiada się o wizualizacjach danych, infografice czy grafice statystycznej, robi się to na przykładach. Przedstawia się ciekawe rozwiązania, czasami z komentarzami. Takie fantastyczne zbiory grafik wartych poznania zbierał Edward Tufte w swoich książkach Envisioning Information [Graphics Press, Cheshire, Connecticut, 1990], Visual Explanations [Graphics Press, Cheshire, Connecticut, 1997], The Visual Display of Quantitative Information [Graphics Press, Cheshire, Connecticut, 2001], Beautiful Evidence [May 2006]. Podobnie skonstruowana jest książka The Functional Art [New Riders, 2012] Alberta Cairo czy Infographics [Wiley, 2012] Jasona Lankowa. W tych książkach autorzy dyskutują swoje rozwiązania, zderzając je z rozwiązaniami innych autorów.
Coraz więcej też można znaleźć katalogów grafik przedstawiających szeroką gamę rozwiązań, często niekoniecznie spójnych merytorycznie. Ciekawe kolekcje takich grafik przedstawione są w atlasach Information is Beatiful [David McCandless. Collins, 2012] czy Around the World [Andrew Losowsky, S Ehmann, and R Klanten. Gestalten, 2013] Przeglądając takie kolekcje, można znaleźć wiele ciekawych rozwiązań. Interesującą pozycją jest też Data Points [Wiley, 2013] Nathana Yau, która jest wyborem interesujących wizualizacji z bloga Flowing Data pogrupowanych w kilka tematycznych kategorii. Osobom, które wolą słuchać narracji do oglądanych obrazków polecam nagranie Cole Nussbaumer Knaflic autorki bloga Storytelling with Data.
Rzadziej można znaleźć książki czy inne źródła, w których przedstawione są zapisy ścieżek, począwszy od szkicu aż do finalnego rozwiązania. Formy pośrednie są najczęściej gorsze od formy finalnej i jest wiele powodów, dla których autorzy nie chcą tych form pośrednich prezentować. Być może chcą utrzymać swój warsztat w tajemnicy, traktując go jako swój osobisty kapitał, może nie chcą być kojarzeni z pokracznymi formami pośrednimi. Potencjalnych powodów jest wiele.
W zakresie wizualizacji danych jedyne znane mi źródło prezentujące takie szkice to blog chartsnthings prowadzony przez Kevina Quealya, pracownika działu graficznego “New York Timesa”. Na tym blogu Kevin pokazuje na zdjęciach, jak wyglądała ścieżka od pomysłu do realizacji dla rozmaitych wizualizacji danych, które są przygotowywane dla internetowego wydania tej gazety. W wielu przypadkach jest to bardzo ciekawa lektura, pokazująca jak dużej zmianie ulegają pierwsze przymiarki zanim przerodzą się w końcowe rozwiązanie i jeżeli chodzi o formę, i o pomysł.
Truizmem jest stwierdzenie, że aby dobrze przekazać informację, musimy ją najpierw sami zrozumieć, a następnie musimy ją przedstawić w sposób pozwalający na jej zrozumienie odbiorcy. Droga od pomysłu do realizacji zawierać więc będzie zarówno elementy, w których staramy się lepiej zrozumieć prezentowaną informację, jak i elementy, w których staramy się ją lepiej pokazać. Ponieważ sam dużo skorzystałem z analizy takich ścieżek, postanowiłem wybrać kilka przykładowych szlaków, które sam przeszedłem, sądząc, że mogą one być interesujące również dla innych.
Prezentowane ścieżki podzieliłem tematycznie na cztery grupy związane z najważniejszymi aspektami opowiadanej historii. Kolejne grupy ścieżek są skupione wokół prezentacji czasu, przestrzeni, niepewności czy otoczenia. Każda z tych ścieżek to próba zejścia z głównego szlaku i odkrycia, co ciekawego jest za kolejnym wzgórzem. Raz będą to alternatywne sposoby pokazywania następstwa zdarzeń w czasie, raz będą to alternatywne sposoby przedstawienia informacji związanej z lokalizacją przestrzenną, raz będą to próby przedstawienia niepewności. Niektóre z tych ścieżek wiodą na manowce, niektóre do ciekawych rozwiązań. To, które są ciekawe, a które błędne, pozostawiam do oceny Czytelnikowi.
 Rysunek 1: Praca z danymi jest iteracyjna, a wizualizacja danych jest pomocna na każdym jej etapie
Rysunek 1: Praca z danymi jest iteracyjna, a wizualizacja danych jest pomocna na każdym jej etapie
Czas
Jakiś czas temu pracowałem nad analizą i prezentacją danych z serwisów społecznościowych takich jak Twitter czy Facebook. Jednym z interesujących mnie zagadnień było, jak często i o jakich porach użytkownicy publikują komentarze na tych serwisach. Czy publikacja ma miejsce o określonych porach, przed czy po pracy, w określone dni tygodnia, czy jest regularna, czy sporadyczna.
Zagadnieniu przedstawiania częstotliwości przyjrzymy się na przykładzie danych o aktywności polityków w serwisie Twitter. Znaczna część polityków ma konto na tym serwisie i osobiście lub z pomocą swojego biura publikuje tam informacje, traktując to jako formę kontaktu z wyborcami. API Twittera pozwala na pobranie historii komunikatów określonego użytkownika, zarówno ich treści, jak i czasów publikacji. Poniżej przyjrzymy się wpisom publikowanym poprzez konto @PremierRP w latach 2010–2011.
Szukając wzorców w częstości występowania jakiegoś zjawiska, zwykle przedstawia się częstości w określonych agregacjach, np. liczba zdarzeń dziennie, miesięcznie czy na godzinę.
Patrząc na dzienną aktywność konta @PremierRP można zauważyć, że lato i wczesna jesień 2011 roku to nie był okres wakacji, ale wzmożonej aktywności na Twitterze.
Śledząc aktywność w rozbiciu na dni tygodnia, można zauważyć wzmożoną aktywność we wtorki i piątki, niższą w poniedziałki (któż lubi poniedziałki w pracy) i znacznie niższą podczas sobót i niedziel.
Analizując aktywność o różnych godzinach, można zauważyć, że pierwsze komunikaty pojawiają się czasem bardzo wcześnie, jeszcze przed godziną 7 rano, pierwszy szczyt aktywności konto osiąga po godzinie 8 rano, a drugi szczyt aktywności przed 17. Komunikacja za pośrednictwem Twittera ma charakter nieformalny, nie są więc zaskakujące wiadomości pojawiające się również bardzo późnym wieczorem.
Jak widzimy, każde z tych ujęć danych pokazuje pewną, czasem interesującą, informację. Zestawienie jednak wszystkich czterech wykresów paskowych obok siebie byłoby dosyć nudne. Wykres paskowy nie jest najwdzięczniejszym medium, cała informacja jest płaska i nie ma gdzie zmieścić hierarchii informacji. Czy można informacje z tych różnych ujęć umieścić na jednym wykresie i do tego tak, by była ona czytelna?
Ciekawym rozwiązaniem jest użycie wykresu kalendarzowego. Na głównym wykresie do zaznaczenia liczby wiadomości wykorzystuje się kolor. Kolor nie jest charakterystyką umożliwiającą dokładne odczytanie wartości, ale pozwala na szybką identyfikację wzorców oraz na większą kompresję treści. Ponieważ rozróżnianie czy w danym dniu pojawiło się trzy czy pięć wiadomości nie jest kluczowe, więc do naszych celów niska precyzja w odczycie liczby wiadomości nie jest przeszkodą.
Z uwagi na wykorzystanie kilku wierszy do prezentacji kolorów łatwiej jest zidentyfikować konkretną datę na wykresie. Patrząc na aktywność w kolejnych dniach, na przedstawionym wykresie wyraźnie wyróżnia się jeden dzień, 18 listopada 2011, w którym to, zaprzysiężono drugi rząd Donalda Tuska, co było oczywiście szeroko komentowane na Twitterze.
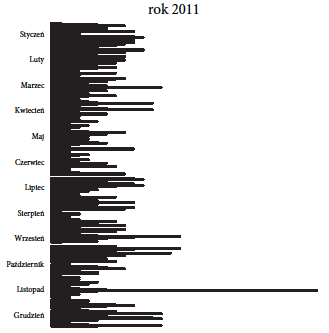 Rysunek 2: Liczba wiadomości publikowanych dziennie przez konto
Rysunek 2: Liczba wiadomości publikowanych dziennie przez konto @PremierRP w roku 2011. Źródło: opracowanie własne
 Rysunek 3: Liczba wiadomości na dzień tygodnia publikowanych przez konto
Rysunek 3: Liczba wiadomości na dzień tygodnia publikowanych przez konto @PremierRP Źródło: opracowanie własne
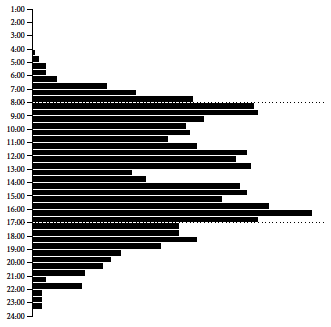 Rysunek 4: Liczba wiadomości publikowanych przez konto
Rysunek 4: Liczba wiadomości publikowanych przez konto @PremierRP o różnych porach dniach, przy użyciu agregacji w pięciominutowych przedziałach. Źródło: opracowanie własne
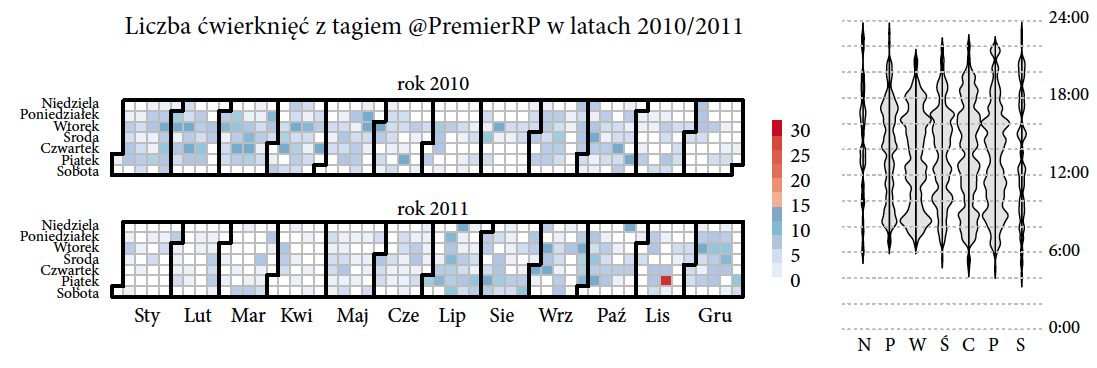 Rysunek 5: Liczba wiadomości na Twitterze z tagiem
Rysunek 5: Liczba wiadomości na Twitterze z tagiem @PremierRP w różnych dniach oraz o różnych porach roku. Źródło: opracowanie własne
Obok wykresu kalendarzowego przedstawiono wykresy skrzypcowe pokazujące natężenie wiadomości publikowanych w określonych godzinach w rozbiciu na dni tygodnia. Szerokość skrzypiec w danym miejscu odpowiada względnej częstości publikowania wiadomości danego dnia o danej godzinie. Większość wiadomości jest w miarę jednostajnie rozproszona w dniach roboczych w godzinach pracy, ale zdarzają się też bardzo wczesne lub bardzo późne komunikaty (ale nie w poniedziałek rano). Format prezentacji zastosowany na wykresie 5 pozwala na zwarte przedstawienie nawet większej ilości informacji niż na poprzednich trzech wykresach paskowych.
W powyższym przykładzie, interesowały nas tylko czasy wystąpienia zjawiska, nie analizowaliśmy treści tych wiadomości. Przyjrzyjmy się teraz innemu przykładowi, w którym poza datami będą nas też interesować informacje o zdarzeniach.
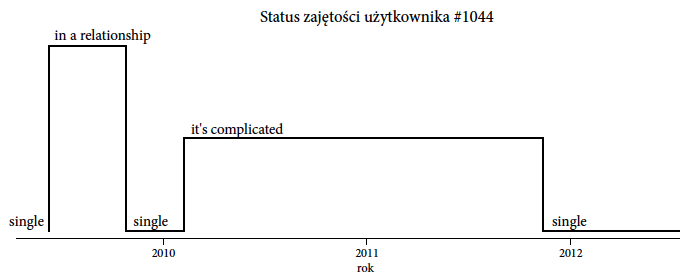
Analizy dotyczą danych, które zostały zebrane i udostępnione na blogu Facemining Wojciecha Walczaka [Wojciech Walczak. Facemining, 2013] Opisują one jak dla wybranych kont w serwisie Facebook zmieniała się w czasie deklaracja bycia w związku, czyli deklarowany status “zajętości” użytkownika. W serwisie Facebook wyróżnia się kilka rodzajów “zajętości”, takie jak: “zaręczony”, “w związku małżeńskim”, “wolny”, czy modne ostatnio “to skomplikowane”. Przyjrzymy się, jak często te deklaracje ulegają zmianom. Ustawiając optykę narzędzia do analiz na jednego użytkownika, można dla niego pokazać za pomocą wykresu w stylu “linii czasu” (wykres 6) historię zmian jego stanu bycia w związku.
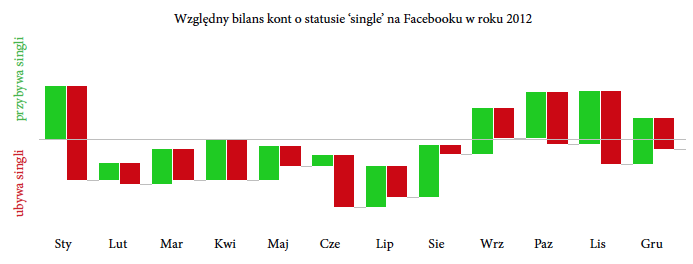
Przestawmy teraz optykę z jednego użytkownika na całą populację. Patrząc na grupę użytkowników, można szukać wzorców dotyczących częstości wchodzenia lub wychodzenia ze stanu singla (wykres 7). Czy przed walentynkami więcej związków jest deklarowanych czy rozwiązywanych na Facebooku?
Rysunek 6: Zmiany deklarowanego związku dla jednego przykładowego użytkownika. Jego status przez dosyć długo był ustawiony na it's complicated, ale koniec końców się uprościł. Źródło: opracowanie własne
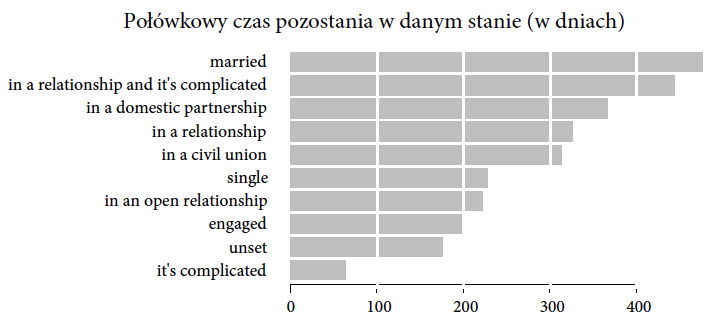
Inna interesująca informacja, którą możemy wyłuskać z danych, to jak długo trwają różne rodzaje związków oraz czym te związki się kończą. Jak często facebookowe narzeczeństwo kończy się facebookowym związkiem małżeńskim, a jak często facebookowym zerwaniem?
Zacznijmy od informacji dotyczącej czasu ich trwania. To ciekawa zmienna, ponieważ nie możemy policzyć dla niej średniej. Nie dla każdej osoby wiemy, jak długo dana relacja trwała, co więcej są pewnie osoby, które w określonym stanie zostają do końca życia
Rysunek 7: Względne zmiany frakcji osób ze statusem single Czerwony pasek opisuje, ilu singli ubyło w danym miesiącu, zielony, ilu singli przybyło. W styczniu (przed walentynkami) i czerwcu (przed wakacjami) znacząco kurczy się pula osób ze statusem singla. Po wakacjach sytuacja wraca do normy. Źródło: opracowanie własne
To, co można jednak policzyć (lub przynajmniej oszacować), to czas półtrwania związku, czyli czas, po którym połowa relacji określonego typu się kończy. Załóżmy, że interesuje nas okres półtrwania relacji “engaged” (zaręczeni). Do oszacowania tego parametru wystarczy, że dla połowy osób, które zadeklarowały stan “engaged” mamy informację, że ten stan się zakończył i użytkownik przeszedł do innego stanu. Nie musimy czekać na zakończenie wszystkich związków typu “engaged”, tak jakby to miało miejsce, gdybyśmy chcieli policzyć średnią. Nawet jeżeli są osoby, które wpadają w stan “engaged” na zawsze, to nie zaburzają one czasu półtrwania związku. O ile oczywiście takich osób jest mniej niż połowa, ale analizujemy związki na Facebooku, a te, jak się okazuje, są nietrwałe.
Poza czasami półtrwania może nas również interesować to, co się dzieje po zakończeniu określonego charakteru relacji. Stan “narzeczeństwo” może zakończyć się przejściem w stan “małżeństwo” lub “wolny” lub “to skomplikowane”. Nie tylko chcemy wiedzieć jak długo przebywa się w danym stanie, ale również jak często przechodzi się z tego do innych stanów.
Rysunek 8: Czasy półtrwania dla określonych typów związków. Źródło: opracowanie własne
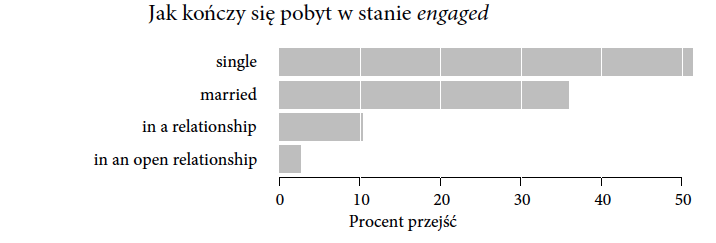
Informacje o tym, do którego stanu przechodzą użytkownicy Twittera, można przedstawić za pomocą wykresów paskowych. Teoretycznie, moglibyśmy taki pasek narysować dla każdej pary możliwych przejść od jednego rodzaju związku do drugiego. To jednak oznaczałoby kilkadziesiąt pasków przedstawiających różne częstości. Oglądanie i porównywanie kilkudziesięciu szarych pasków jest dosyć nudnym zajęciem. Jak więc przedstawić tę informację w zwartej i ciekawej postaci?
W gruncie rzeczy, chcemy pokazać, jak wyglądają przejścia pomiędzy różnymi stanami “zaawansowania” związku, a do przedstawienia informacji o zmianach stanu można wykorzystać grafy opisujące warianty łańcuchów Markowa. I choć opisywany model relacji nie jest łańcuchem Markowa (w łańcuchach Markowa zakłada się, że prawdopodobieństwo przejścia do kolejnego stanu nie zależy od przeszłych stanów, co w przypadku relacji międzyludzkich jest dużym uproszczeniem), to możemy go w podobny sposób przedstawić.
Rysunek 9: Jak kończy się pobyt w stanie engaged W ponad połowie przypadków następuje przejście do stanu single, niewiele mniej przypadków kończy się jako married Źródło: opracowanie własne
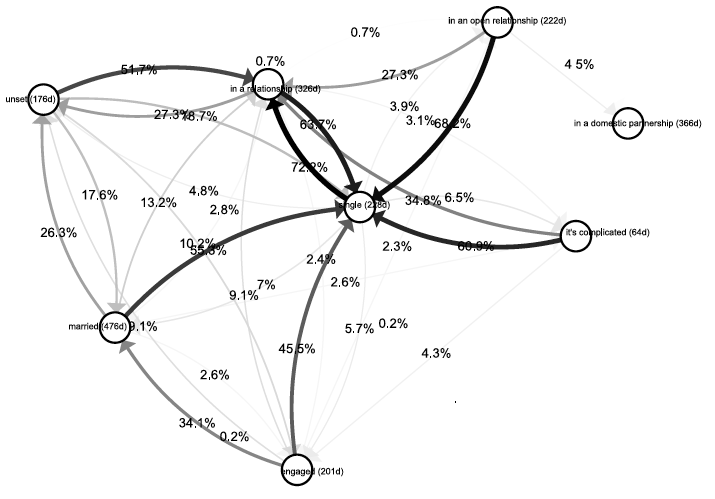
Po przedstawieniu całego grafu możliwych przejść okazuje się, że liczba różnych scenariuszy jest duża, przez co cała grafika jest dosyć skomplikowana. Stanów jest wiele, ale niektóre są bardzo rzadko odwiedzane (przykładowo “in a domestic partnership”). Sieć przejść pomiędzy stanami jest gęsta, choć dla wielu krawędzi prawdopodobieństwa przejść są bardzo bliskie zeru.
Rysunek 10: Macierz opisująca przejścia pomiędzy stanami. Zaznaczono wszystkie stany i wszystkie krawędzie, które wystąpiły w zbiorze danych. Z uwagi na mnogość elementów na wykresie trudno szybko odnaleźć ważne stany i krawędzie. Źródło: opracowanie własne
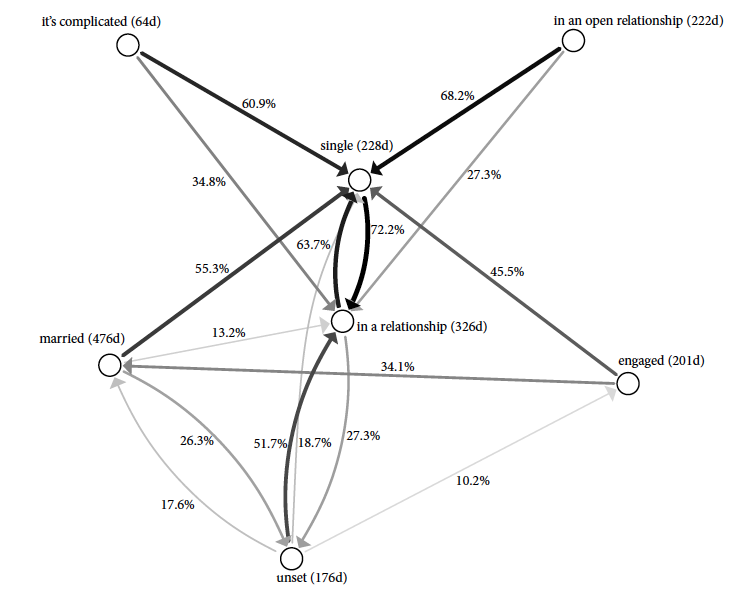
Kosztem dokładności i pełności opisu możemy ten graf znacznie uprościć, przedstawiając tylko najczęstsze węzły oraz najczęstsze krawędzie, na przykład przyjmując próg dla rysowania krawędzi, które mają prawdopodobieństwo przejścia równe przynajmniej 10%. Samemu wykresowi dobrze też zrobi kilka kosmetycznych zabiegów, takich jak zmiana kroju pisma czy wielkości elementów wykresu.
W obu powyższych przykładach przedstawialiśmy informacje o częstości pewnego zjawiska, za każdym razem robiliśmy to w inny sposób. Przyjrzymy się teraz innemu zjawisku, w którym też będziemy oglądać częstość, ale na przestrzeni nie kilku, a kilku tysięcy lat. Przyjrzymy się, jak wygląda czas trwania pontyfikatu papieskiego.
W lutym 2013 roku, krótko przed zakończeniem ósmego roku pontyfikatu, papież Benedykt XVI abdykował. W okresie pomiędzy abdykacją a konklawe wyłaniającym nowego papieża, ze zrozumiałych powodów, temat długości pontyfikatu stał się bardzo medialny. W mediach przedstawiano przykłady najkrótszych i najdłuższych pontyfikatów, przez co i mnie zainteresował temat czasu trwania pontyfikatu, ale nie średniego czasu trwania, tylko całego rozkładu czasu trwania pontyfikatów.
Informacje o pontyfikatach papieży można pobrać z serwisu
[The Original Catholic Encyclopedia.
List of popes, 2013] Bazując na tych danych, przyjrzyjmy się, jak długo trwały pontyfikaty papieży na przełomie dwóch tysiącleci.
Rysunek 11: Macierz opisująca przejścia pomiędzy stanami. Usunięcie rzadkich krawędzi zwiększyło czytelność, choć może budzić wątpliwości u osób, które dostrzegają, że nie zawsze wychodzące krawędzie sumują się do 100%. Źródło: opracowanie własne
Rysunek 12 przedstawia rozkład długości trwania pontyfikatu. Pokazano, dla jakiej części papieży pontyfikat trwał dłużej niż x lat. Nie wiemy jednak, którzy papieże mieli krótkie, a którzy mieli długie pontyfikaty. Czy pontyfikaty kiedyś były dłuższe czy krótsze niż obecnie? Czy były w historii okresy ze szczególnie dużą zmiennością na tronie Piotrowym?
A jak zobaczyć, w których wiekach pontyfikaty były krótkie, a w których były długie? Z problemu pokazania długości pontyfikatu spróbujmy przejść do problemu odwrotnego, przedstawiania częstości powołań nowych papieży, np. na jednostkę czasu, powiedzmy na stulecie.
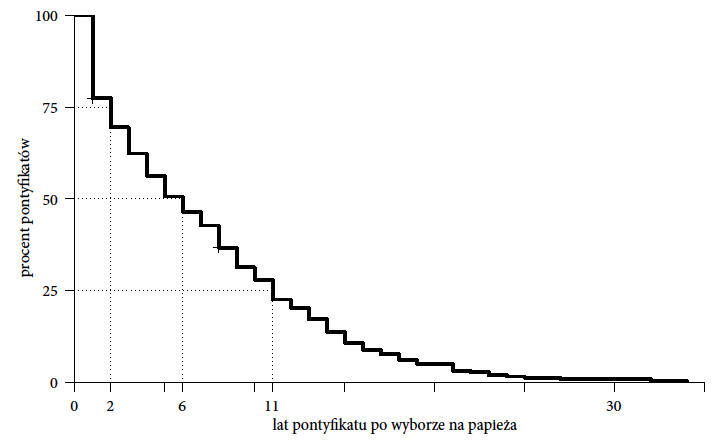
Rysunek 12: Rozkład czasu trwania pontyfikatu. Na osi poziomej zaznaczono czas w latach, a wysokość krzywej w danym punkcie odpowiada procentowi papieży, których pontyfikat trwał tyle lub więcej lat. Wyróżnione punkty pokazują, że 1/4 pontyfikatów była krótsza niż dwa lata, 50% pontyfikatów było krótszych niż 6 lat a 1/4 było dłuższych niż 11 lat. Źródło: opracowanie własne
Taką informację można przedstawić za pomocą modyfikacji wykresu paskowego, na którym zaznaczymy zarówno liczbę papieży powołanych w danym stuleciu, jak i dodatkowe informacje o tym, którzy papieże zostali później uznani za błogosławionych lub świętych. Z takiej prezentacji można szybko odczytać zarówno okresy, w których pontyfikaty były krótkie (czasem w jednym stuleciu “zmieściło się” ponad dwadzieścia pontyfikatów), jak i okresy “bogate” w świętych (najwięcej papieży uznanych za świętych było w pierwszych pięciu wiekach, po dziewiątym wieku papieże uznani za świętych stanowią rzadkość).
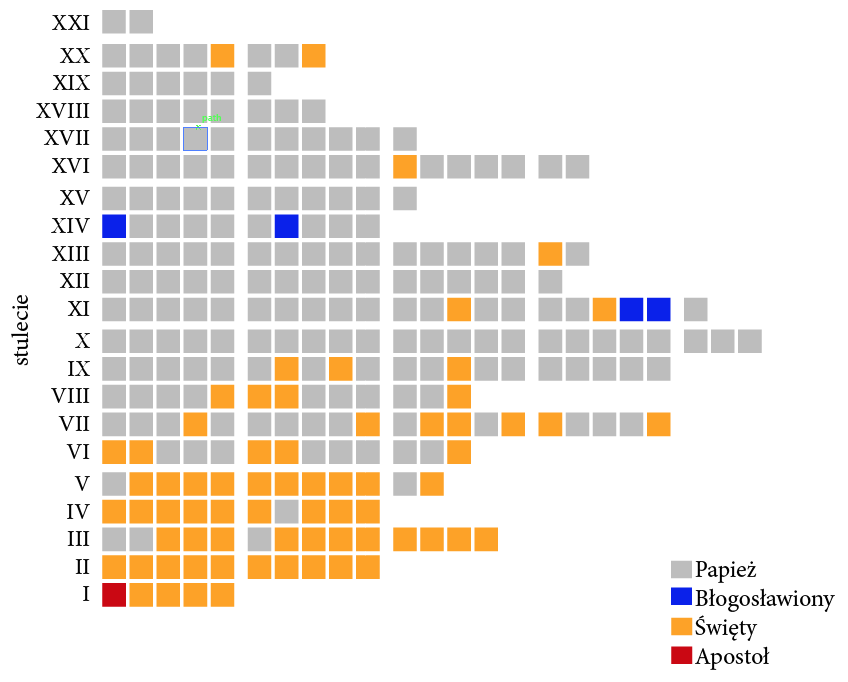
A czy można na jednym wykresie umieścić jeszcze więcej informacji, nie zwiększając zbytnio jego komplikacji? Taką próbę podjęto na wykresie 14. Zaznaczono dodatkowo imiona papieży, ponadto optycznie łatwo ocenić liczbę papieży w wierszu, dzięki czemu zachowujemy informację z poprzedniego wykresu, a z odstępów pomiędzy papieżami można odczytać czas trwania pontyfikatu (o ile nie trafia się w przełom wieków) oraz orientacyjne daty rozpoczęcia i zakończenia pontyfikatu. Kolor, podobnie jak na poprzednim wykresie, opisuje, czy papież został ogłoszony świętym lub błogosławionym.
Rysunek 13: Liczba powołań na papieża w kolejnych stuleciach. Oznaczając kolorem papieży błogosławionych i świętych dodatkowo łatwiej zauważyć wzorce dotyczące kanonizacji głów kościoła lub długości pontyfikatów. Dzięki zastosowaniu dodatkowego pionowego odstępu co pięć kratek można szybko odczytać liczbę pontyfikatów nawet pomimo braku osi z zaznaczonymi wartościami liczbowymi. Źródło: opracowanie własne
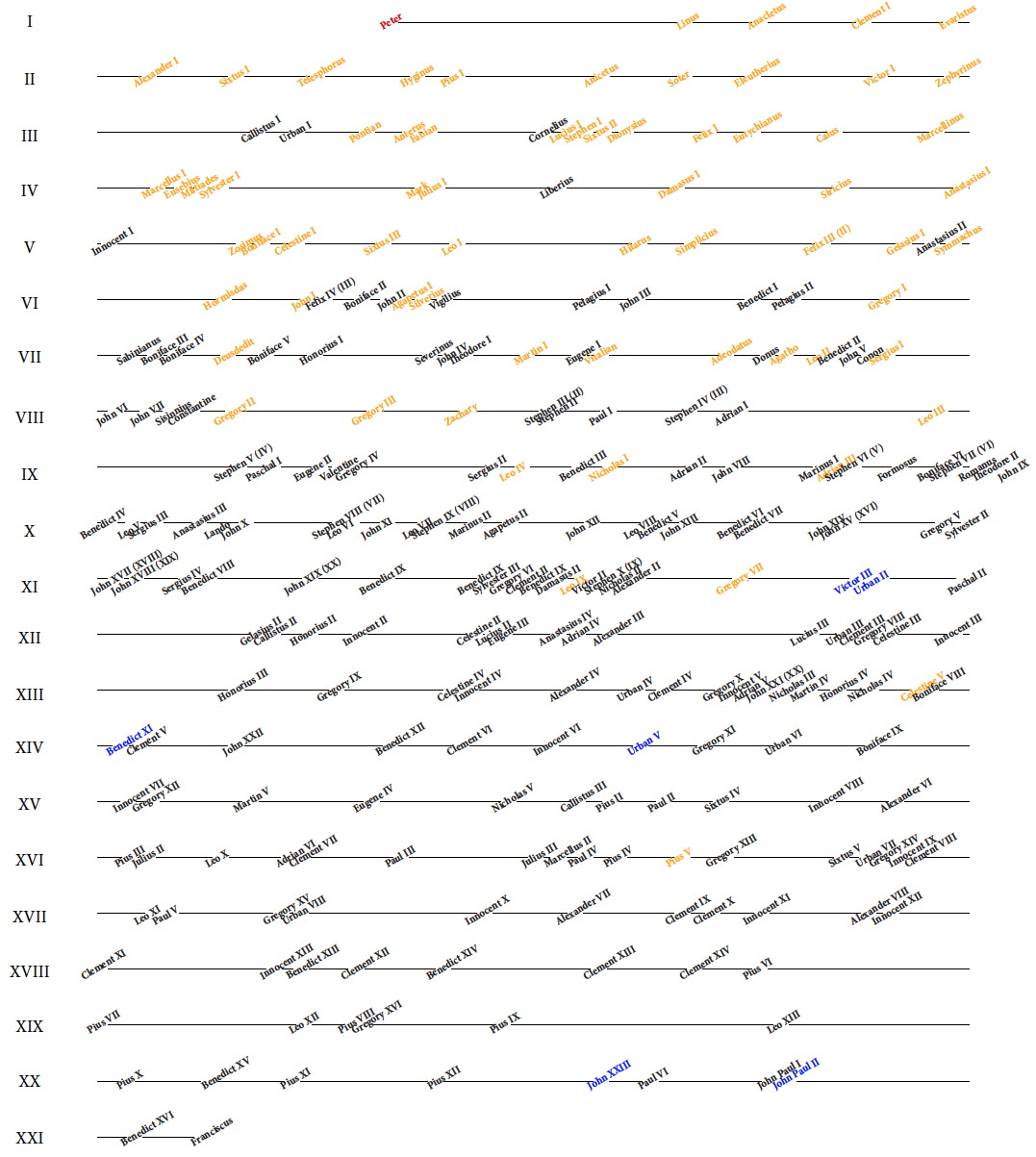 Rysunek 14: Pontyfikaty papieży papieży w kolejnych stuleciach. Źródło: opracowanie własne
Rysunek 14: Pontyfikaty papieży papieży w kolejnych stuleciach. Źródło: opracowanie własne
Przestrzeń
Dużo mówi się o tym, że żyjemy w globalnej wiosce i że świat się skurczył. I na wielu przykładach można uzasadniać, że tak w istocie jest. Są jednak sytuacje, w których to lokalne otoczenie odgrywa znaczącą rolę.
Dwa przykłady ilustrujące, jak ważne jest najbliższe otoczenie, to edukacja podstawowa (nauczanie podstawowe przez Internet nie jest w każdym bądź razie w Polsce zbyt popularne i niewiele osób decyduje się wozić dziecko daleko do podstawówki) oraz służba zdrowia (turystyka medyczna jest coraz bardziej popularna, ale wciąż dotyczy małej części społeczeństwa, większość korzysta z okręgowych lekarzy). Skoro lokalność tych dwóch typów usług jest tak istotna, to ciekawym będzie przyjrzenie się, jak wygląda zróżnicowanie jakości tych usług w różnych obszarach czy to kraju, czy miasta.
Zacznijmy od podstawówek. Wybór szkoły podstawowej dla wielu rodziców jest sprawą na tyle ważną, że gotowi są przeprowadzić się do innej dzielnicy, by upatrzona podstawówka stała się szkołą rejonową ich dziecka. Ta presja czasem związana jest z chęcią wysłania dziecka do szkoły, do której chodzą dzieci “odpowiednich” rodziców, czasem z chęcią wysłania dziecka do szkoły, która ma najwyższe wyniki w rejonie, czasem do szkoły, w której wychowuje się zgodnie z określonymi wartościami. Motywy mogą być przeróżne (Dotyczy to wielu rodziców, ale oczywiście nie większości. Zjawisko tez jest bardziej nasilone w Warszawie niż w innych miastach, daleko nam też do tego co skłonni są zrobić dla edukacji dzieci rodzice w Korei).
Abstrahując zupełnie od tego, czy warto wybierać dla dziecka szkołę, w której w ostatnim roku dzieci miały wysokie wyniki na egzaminie (co często jest spowodowane tym, jakie rodziny mieszkają w okolicy lub przypadkowymi fluktuacjami), zobaczmy, jak można prezentować informację o średnich wynikach szkół. Do opisu wyników szkoły użyjemy średniej z wyniku egzaminu szóstoklasisty.
Zazwyczaj średnie wyniki egzaminów szóstoklasistów prezentowane są przez Okręgowe Komisje Egzaminacyjne w tabelarycznych zestawieniach: liczba uczniów, średni wynik szkoły, nazwa i adres podstawówki. Taka forma jest wygodna do publikacji, ale trudna do wykorzystania przez zainteresowanego rodzica. W przypadku dużego miasta, które ma kilkadziesiąt szkół podstawowych, nawet dla osoby doskonale znającej każdą ulicę w mieście lokalizacja najbliższych podstawówek nie jest prosta. Przyjezdni mają jeszcze gorzej, ponieważ części adresów mogą nie znać. A to właśnie lokalizacja dobrej szkoły w niedużej odległości od miejsca zamieszkania jest najciekawszą informacją dla rodzica.
Dosyć naturalnym wyborem jest umieszczenie informacji o wynikach szkół podstawowych na mapie miasta. Niewiele osób chciałoby codziennie dowozić dziecko kilkanaście kilometrów do szkoły, więc obszar w skali kilku kilometrów wydaje się być rozsądnym wyborem.
Trudnym zadaniem okazało się przedstawienie jednocześnie lokalizacji, wielkości oraz średniego wyniku egzaminu dla szkoły (wszystko to zmienne w skali ilościowej). Jeżeli przyjąć, że szkołę przedstawiać będziemy za pomocą symboli, to zmienne możemy mapować na położenie, wielkość, kształt, kolor lub fakturę symbolu. Szybko okazuje się, że dla takiej liczby szkół używanie kształtów lub faktur jest bardzo niewygodne. W przypadku średniego wyniku ostatecznie zdecydowałem się na kodowanie z użyciem kolorów. Dla osób z problemami w rozróżnieniu kolorów może to powodować trudności, ale przypadłość ta jest rzadka i stwierdziłem, że któreś z rodziców będzie w stanie poprawnie tę informację odczytać.
Wyniki z egzaminu obarczone są pewną losowością, a im mniejsza szkoła, tym losowość wynikająca z rozmiaru próby jest większa. Aby rozróżnić duże szkoły od małych, wielkością koła oznaczałem liczbę szóstoklasistów, która pośrednio również odpowiada wielkości szkoły.
Najtrudniejsze okazało się wybranie sposobu prezentacji umożliwiającego łatwe wyszukanie, gdzie znajduje się określona szkoła. Mapy prezentowane przez serwisy Google Maps lub Open Street Maps okazały się zbyt szczegółowe, by służyć za drugoplanowe tło. Pomocne okazały się mapy opracowane przez firmę Stamen design, wśród których znalazła się mapa w schemacie “watercolor” o niewielkiej liczbie szczegółów, głównie będących obrysami największych ulic, które nie kolidują z symbolami oznaczającymi szkoły, a pozwalają na szybką orientacyjną lokalizację szkoły.
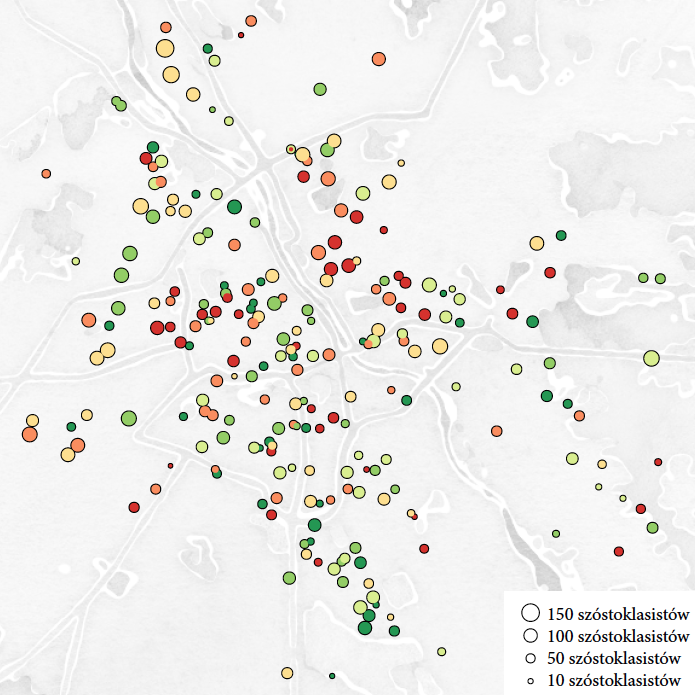
Po zamianie palety kolorów na odcienie szarości i po przesunięciu rozjaśnionej mapy na drugi plan udało się uzyskać zadowalającą czytelność przy małym natłoku nadmiernych szczegółów. Wyszarzenie i rozjaśnienie mapy jako tła ułatwia odczytanie koloru kropek na pierwszym planie, można zauważyć całe dzielnice w których występuje nagromadzenie szkół o wysokich/niskich średnich, co sugeruje, że wyniki są raczej związane z zamożnością i wykształceniem rodziców niż z efektem poszczególnej szkoły. Przyjęta skala kolorów (ciemnoczerwony dla szkół o niskiej średniej, ciemnozielony dla szkół o wysokiej średniej) jest intuicyjna. Informacja o wielkości szkoły jest trudna do precyzyjnego odczytania, wystarcza jednak do identyfikacji dużych i małych szkół, a w tym przypadku wielkość szkoły jest zmienną drugoplanową.
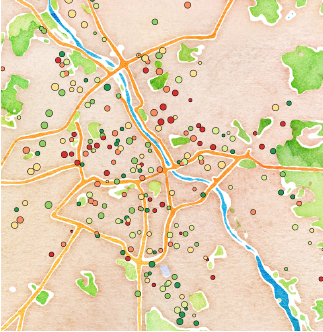 Rysunek 16: Wyniki z egzaminu szóstoklasisty naniesione na mapę “watercolor” z serwisu Stamen Maps. Mapa wygląda ciekawie, jak malowana akwarelami. Usunięcie zbędnych szczegółów, takich jak małe ulice, pozwala na skoncentrowanie się na szkołach. Akwarelowe kolory kolidują jednak ze skalą kolorów użytą do oznaczania, które szkoły mają dobre, a które złe wyniki. Źródło: opracowanie własne
Rysunek 16: Wyniki z egzaminu szóstoklasisty naniesione na mapę “watercolor” z serwisu Stamen Maps. Mapa wygląda ciekawie, jak malowana akwarelami. Usunięcie zbędnych szczegółów, takich jak małe ulice, pozwala na skoncentrowanie się na szkołach. Akwarelowe kolory kolidują jednak ze skalą kolorów użytą do oznaczania, które szkoły mają dobre, a które złe wyniki. Źródło: opracowanie własne
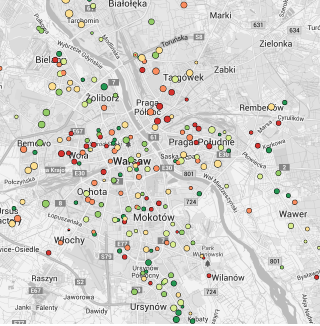 Rysunek 17: Wyniki z egzaminu szóstoklasisty naniesione na mapę pobraną z serwisu Google Maps. Duża liczba szczegółów na mapie utrudnia dostrzeżenie wzorców w wielkości i wynikach szkół, ale ułatwia lokalizację poszczególnych podstawówek. Źródło: opracowanie własne
Rysunek 17: Wyniki z egzaminu szóstoklasisty naniesione na mapę pobraną z serwisu Google Maps. Duża liczba szczegółów na mapie utrudnia dostrzeżenie wzorców w wielkości i wynikach szkół, ale ułatwia lokalizację poszczególnych podstawówek. Źródło: opracowanie własne
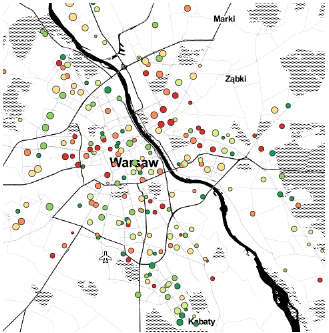 Rysunek 18: Wyniki z egzaminu szóstoklasisty naniesione na mapę “Toner”. Duży kontrast na mapie ułatwia szybką orientację, zwłaszcza gdy przyjmie się Wisłę jako punkt odniesienia. Jednocześnie wyraźnie oznaczone drogi zaburzają pierwszy plan, na którym trudniej zobaczyć informacje o szkołach. Źródło: opracowanie własne
Rysunek 18: Wyniki z egzaminu szóstoklasisty naniesione na mapę “Toner”. Duży kontrast na mapie ułatwia szybką orientację, zwłaszcza gdy przyjmie się Wisłę jako punkt odniesienia. Jednocześnie wyraźnie oznaczone drogi zaburzają pierwszy plan, na którym trudniej zobaczyć informacje o szkołach. Źródło: opracowanie własne
Do podstawówki dzieci chodzą codziennie, dlatego każdy kilometr pomiędzy miejscem zamieszania a podstawówką robi różnicę. Ale co z usługami, z których korzystamy rzadziej, na tyle, że odległość ma mniejsze znaczenie? Przykładem takich usług jest dostęp do lekarzy specjalistów.
Na stronach NFZ publikowane są informacje statystyczne o czasach oczekiwania do specjalistów wraz z informacją o liczbie osób w kolejce. Dane są dostępne w postaci tabeli w pliku Excela, a więc z wyszukiwaniem najbliższych poradni mamy ten sam problem, co w przypadku danych o wynikach egzaminu w szkołach podstawowych.
Rysunek 19: Wyniki z egzaminu szóstoklasisty naniesione na rozjaśnioną i wyszarzoną mapę ze schematu “watercolor”. Źródło: opracowanie własne
Zaczniemy od pytania, jak wygląda średni czas oczekiwania w kolejce do specjalisty. Biorąc pod uwagę wizję kilkunastomiesięcznego czasu oczekiwania do niektórych specjalistów, chory może rozważyć nawet wyjazd do innego miasta. Obszar, który rozważa osoba pilnie szukająca specjalisty, obejmować może dziesiątki kilometrów.
Dla ustalenia uwagi skupimy się na lekarzach alergologach. Na rysunku 20 przedstawiono położenie geograficzne poradni ze specjalistami alergologami wraz z informacją o średnim czasie oczekiwania zakodowanym za pomocą koloru.

Z tą mapą jest jednak kilka problemów. Pierwszy dotyczy dużych miast, w których jest kilka poradni. Kropki odpowiadające różnym poradniom nakładają się na siebie, przez co części poradni nie widzimy. Drugi problem dotyczy niestabilności w czasie tych wyników. Mają one tendencje do zmian z miesiąca na miesiąc.
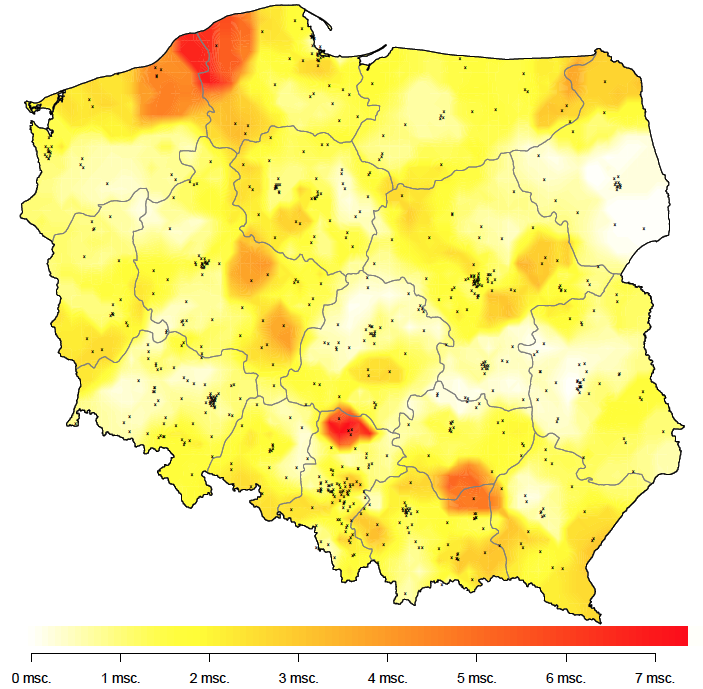
Bardziej pożądana byłaby informacja agregująca wyniki z najbliższych poradni. Jednym z pomysłów jest wyznaczenie dla każdego punktu na mapie pięciu najbliższych poradni, a następnie wyliczenie średniego czasu oczekiwania w tych najbliższych pięciu poradniach. Taką informacje przedstawiamy na rysunku 21.
Są obszary, w których kolejki do specjalisty są wyjątkowo długie, w tym przykładzie są to okolice Częstochowy i Słupska. Skala oparta o kolory ma tę zaletę, że łatwo zauważyć plamę o wyróżniającej się jasności, ale też tę wadę, że trudniej jest odczytywać wartości nawet mając do pomocy legendę.
Postrzegana intensywność koloru zależy od otoczenia i nasze oko może mieć problem z dopasowaniem kolorów do legendy, a nie ma podręcznych sposobów, by przystawić wzornik koloru do wskazanego miejsca na wykresie.
Rysunek 20: Graficzna prezentacja danych o średnim czasie czekania do lekarza specjalisty alergologa. Zielony kolor wskazuje miejsca o dużej a czerwony, o małej dostępności. Źródło: opracowanie własne
Co może być alternatywą dla koloru? Na przykład wielkość punktu. Mniej kolorowy, ale łatwiejszy w odczytaniu wykres 22 używa wielkości punktu do zaznaczenia informacji o czasie oczekiwania na wizytę.
Rysunek 21: Graficzna prezentacja danych o średnim czasie czekania do lekarza specjalisty alergologa. Im ciemniejszy kolor, tym dłuższy czas oczekiwania. Źródło: opracowanie własne
W tym miejscu warto zadać pytanie, czy średni czas oczekiwania to najciekawsza charakterystyka do przedstawienia? Jeżeli zależy nam na szybkiej wizycie u alergologa, to informacja o tym, że w okolicy trzeba czekać średnio pięć miesięcy jest mniej ciekawa, niż informacja jak daleko muszę jechać, by mieć wizytę w tym miesiącu. Zobaczmy więc, czy w Polsce są pustynie dostępności do lekarza alergologa.
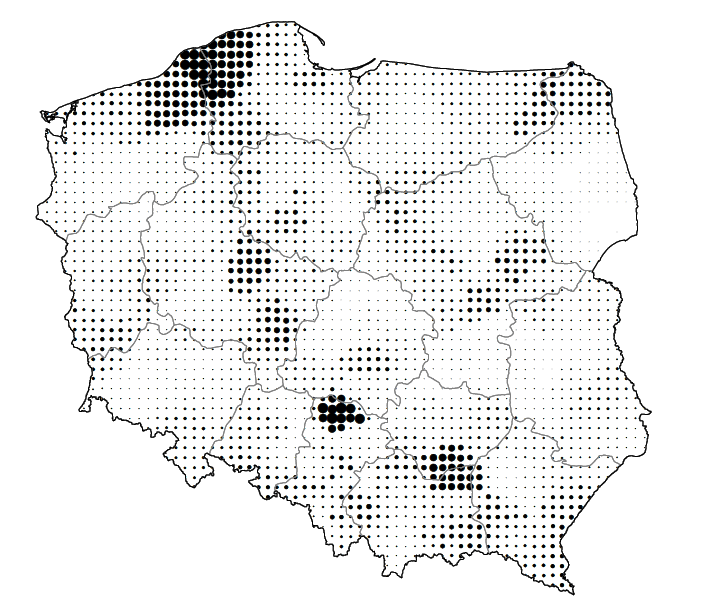
Rysunek 22: Średni czas czekania do lekarza specjalisty alergologa oznaczony za pomocą wielkości punktu. Źródło: opracowanie własne
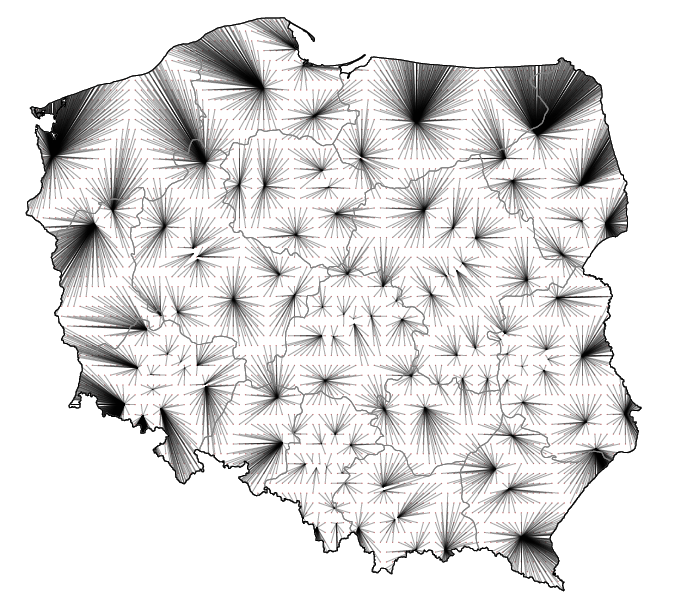
Na wykresie 23 za pomocą odcinków przedstawiono, jak daleko pacjenci z danej lokalizacji mają do najbliższej przychodni, w której czas oczekiwania jest mniejszy niż dwa tygodnie, oraz w którym kierunku należy jechać.
Ten sposób prezentacji ma kilka zalet. Obszary, z których do specjalisty jest daleko, są wyraźnie widoczne, ponieważ długie odcinki tworzą duże łatwo dostrzegalne plamy. Jasne obszary, to miejsca, skąd do najbliższego specjalisty jest relatywnie blisko, te białe plamy również są widoczne.
Zauważmy, że informacje przedstawione na mapie odległości do najbliższego dostępnego lekarza i mapie średniego czasu oczekiwania różnią się bardzo. W przypadku Częstochowy mapa średniego czasu oczekiwania w kolejce pokazywała duże średnie czasy oczekiwania, ponieważ w okolicy jest dużo przychodni z alergologami i wystarczy, że część z nich ma wyjątkowo długie czasy oczekiwania, by przełożyło się to na wysoką średnią. Ale przychodni w okolicy jest wiele i znajdzie się wśród nich też taka z krótszym czasem oczekiwania, więc na wykresie przedstawiającym odległość do najbliższego dostępnego lekarza te odległości są krótkie.
Rysunek 23: Odległość do najbliższego specjalisty alergologa dostępnego w czasie krótszym niż 14 dni. Każda linia łączy określony punkt mapy ze współrzędnymi przychodni, w której kolejka jest krótsza niż 14 dni. Źródło: opracowanie własne
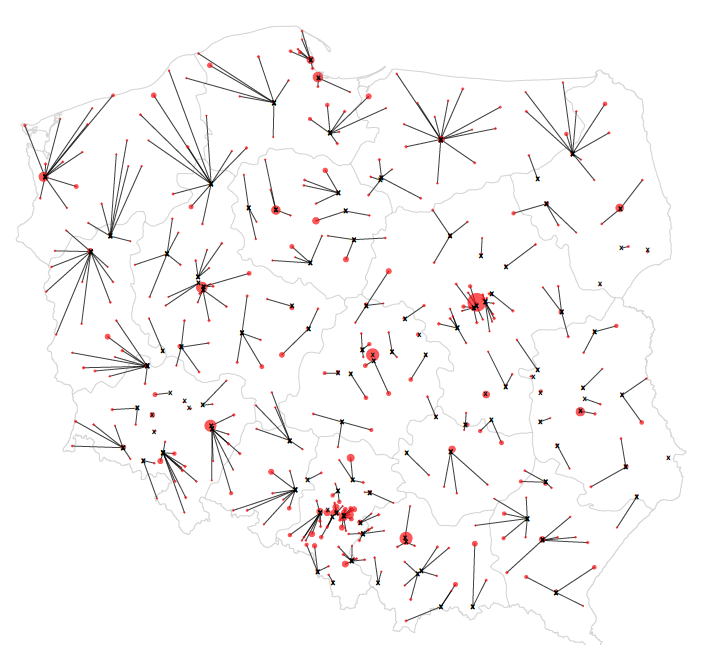
Są w tej formie prezentacji jednak i problemy. Jeden z nich polega na tym, że nie uwzględnia ona gęstości zamieszkania ludzi w różnych rejonach Polski. Zaciemnienie w okolicy Suwałk i duża odległość do specjalisty niekoniecznie jest poważnym problemem, jeżeli gęstość zaludnienia w tej okolicy jest niska. Brak przychodni ze specjalistą w głębokich Bieszczadach jest związany z niskim zaludnieniem, a nie z systematycznym niedofinansowaniem alergologów w tym rejonie.
Jak uwzględnić na tej mapie gęstość zaludnienia? Jedną z możliwości jest rozpoczynanie odcinków w miastach o znacznej ludności, a nie według równo rozmieszczonej kraty. Obszary słabo zaludnione, w których miast jest niewiele lub miasta są małe, nie będą sztucznie generować czarnych plam.
Z kolei wadą tej prezentacji jest brak harmonii i regularności. Odcinki sprawiają wrażenie chaotycznie rozrzuconych i bez szerszego opisu ten wykres może być trudny w odczytaniu. Przynajmniej w skali całego kraju. Jeżeli pokazać bliżej wybrany region, to mapa staje się czytelniejsza.
Rysunek 24: Odległość do najbliższego specjalisty alergologa dostępnego w czasie krótszym niż 14 dni. Odcinki łączą środki miast (wielkość miasta oznaczona wielkością czerwonej kropki) z najbliższą poradnią alergologiczną o kolejce mniejszej niż 14 dni. Wykres ten przedstawia bogatszą informację niż poprzedni. Przez to, że zaznaczone są miasta, łatwo zlokalizować dostępne poradnie specjalistyczne. Źródło: opracowanie własne
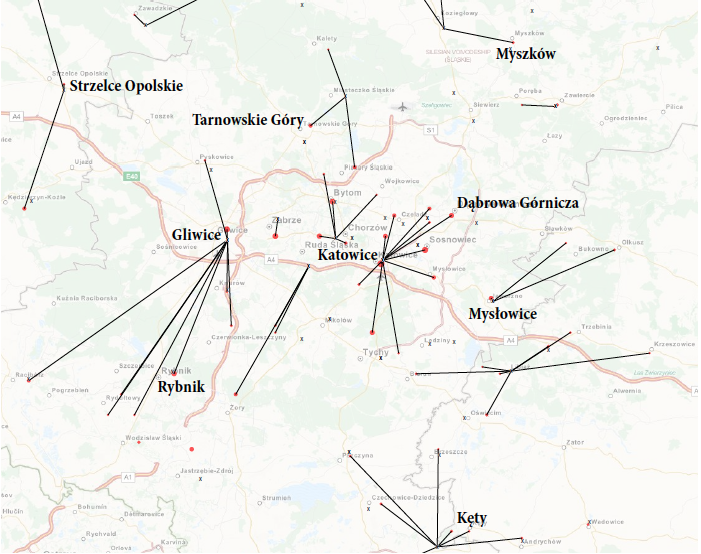
Rysunek 25: Odległość do najbliższego specjalisty alergologa dostępnego w czasie krótszym niż 14 dni. Okolice Katowic. Odcinki łączą środki miast z najbliższą poradnią z dostępnym alergologiem. W tle wykorzystano mapę z serwisu
www.openstreetmap.org Źródło: opracowanie własneNiepewność
Moim zdaniem największym wyzwaniem w prezentacji danych jest informowanie o niepewności prezentowanych wartości. Z jednej strony, większość z nas zdaje sobie sprawę z roli przypadku i niedokładności oceny pewnych wartości (szczególnie, gdy dotyczą one zagadnień społecznych). Z drugiej strony nie potrafimy myśleć i intuicyjnie operować na niepewności i prawdopodobieństwie, a nasza potrzeba prostoty zależności sprawia, że zbyt często lekceważymy wpływ niepewności na efekty naszych działań.
Aby uprościć jakiś komunikat, często pomijamy tę jego część, która opisuje, jak precyzyjnie określone wartości są wyznaczane. Sprawdzając prognozę pogody większość z nas przedłoży komunikat 15 C nad komunikat 95% przedział ufności dla temperatury to 11 C - 19 C.
Niestety większość wartości, które mierzymy, mierzymy z określoną dokładnością. Czasem niewielką. Zapominanie o tym potencjalnym błędzie pomiarowym może być przyczyną błędnych wniosków lub decyzji. Zilustrujemy tę kwestię na przykładzie sondaży wyborczych, które są świetnym przykładem problemów w prezentacji i interpretacji danych obarczonych znaczną niepewnością.
Ze strony agencji Millward Brown, poświęconej badaniom poparcia dla partii politycznych można pobrać wyniki ostatnich 56 (na dzień dzisiejszy) sondaży przeprowadzonych przez tę agencję. Zacznijmy od przedstawienia wyników sondażu z dnia 15 IX 2013.
Wyniki sondaży są zazwyczaj przedstawiane z użyciem wykresów słupkowych/paskowych, więc prezentacja wyników tego sondażu mogłaby wyglądać jak na rysunku 26.

Tego typu przedstawienie danych ma jednak wiele wad. Jedną z nich jest brak łatwej w odczytaniu informacji o dokładności pomiaru, a dla typowej wielkości próby (około 1000 respondentów) pomiary poparcia obarczone są kilkuprocentową niedokładnością. Gdyby nie niepewność pomiaru, obserwowaną zmianę sondażowego poparcia dla PiS o 3% można zinterpretować jako kolosalną zmianę jak na okres pięciu dni, który minął od poprzedniego sondażu z dnia 10 IX 2013.
Aby zaprezentować kontekst, bardziej techniczne portale pokazują też wyniki poprzednich sondaży. Zazwyczaj prezentuje się wyniki kilku poprzednich sondaży, rozciągając znacząco poziomą oś, przez co trudniej zauważyć widoczny błąd pomiaru, objawiający się pojedynczymi “skokami” poparcia. W ten sposób prezentowanych jest ostatnie dziesięć sondaży na portalu http://sondaz.wp.pl/.
Takie rozciągnięcie osi poziomej i łączenie odcinkami wyników kolejnych sondaży sprawia wrażenie, że zmiana poparcia zachodzi powoli, ale systematycznie na określonym odcinku czasu. Czy tak jest? Zobaczymy, jak poparcie zmieniało się na przestrzeni trzech lat.
Rysunek 26: Wynik sondażu z dnia 15 IX 2013 oraz zmiana poparcia w porównaniu do sondażu z dnia 10 IX 2013. Źródło: opracowanie własne
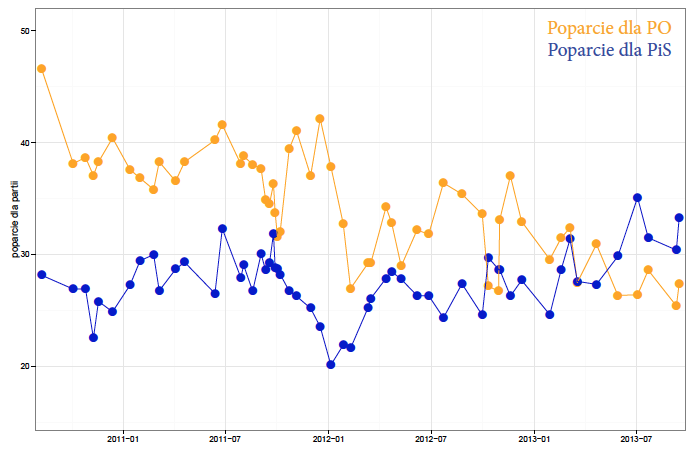
Mając trzy lata historii ściśnięte do jednego wykresu, łatwo zauważyć, że oceny poparcia nie zmieniają się w sposób gładki. Na wykresie wydać czasem pojedyncze skoki “wystające” ponad sąsiednie pomiary. Przykładem są wyniki z 21 kwietnia 2013, gdy to poparcie dla PiS “skoczyło” o ponad 3%, by natychmiast spaść o 4%.
Oczywiście ta losowość próby nie jest niczym niespodziewanym. Problemem powyższych prezentacji jest jedynie to, że w żaden sposób się tej losowości nie zaznacza.
Najbardziej techniczne portale (w tym cytowany portal SMG/KRC MillawardBrown) prezentujące wyniki badań poparcia partii politycznych tę niepewność związaną z pomiarem pokazują poprzez przedziały ufności wokół oceny punktowej.
Problem z takim sposobem prezentacji (zobacz rysunek 28) polega jednak na tym, że widząc procenty poparcia, koncentrujemy na nich uwagę i informacja o przedziale ufności, będąca na dalszym planie, jest często ignorowana. To jeden z klasycznych problemów, gdy twórca wykresu umieszcza pewną informację na wykresie w sposób uniemożliwiający jej dotarcie do odbiorcy. Wiele osób zignoruje informację o dokładności, natomiast samo, dobrze widoczne, średnie poparcie odczyta jako przesadnie dokładne.
Rysunek 27: Wyniki 56 sondaży poparcia dla partii politycznych przeprowadzonych przez Millward Brown w okresie sierpień 2010 – wrzesień 2013. Źródło: opracowanie własne
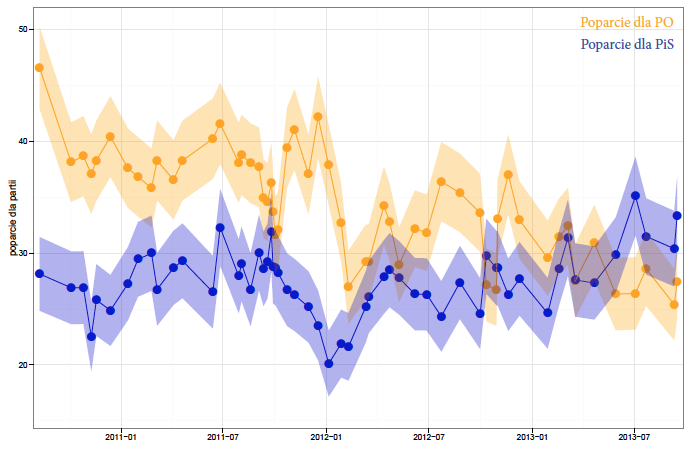
W jaki inny sposób można pokazać niepewność? Jednym z ciekawych rozwiązań jest rozmywanie linii przedstawiającej trend, stosowane czasem przy prezentacji predykcji dla szeregów czasowych. Widząc takie rozmazane pasmo, natychmiast uświadamiamy sobie niepewność, również nasza uwaga nie skupia się na punktowych ocenach, bo te po prostu nie są widoczne (zobacz rysunek 29).
Rysunek 28: Wyniki 56 sondaży poparcia dla partii politycznych przeprowadzonych przez Millward Brown w okresie sierpień 2010 – wrzesień 2013 z zaznaczonym 90% przedziałem ufności dla poparcia. Źródło: opracowanie własne
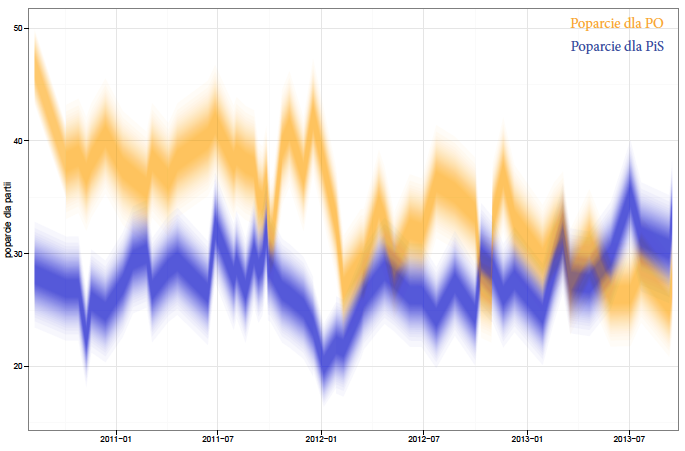
Wadą takiego sposobu prezentacji danych jest jednak brak intuicyjnie widocznego związku pomiędzy stopniem pokrycia z szerokością przedziału ufności. Gdzie zaczyna się to 90% pokrycie, gdzie jest 50% pokrycie? Nasze oko nie jest najlepsze w precyzyjnej ocenie stopnia przezroczystości czy też intensywności koloru.
Wszystkie przedstawione powyżej wizualizacje mają jeszcze jedną wadę. Wyniki dla kolejnych sondaży łączą odcinkami, przez co:
a) sugerują, że pomiędzy sondażami poparcie zmieniało się w sposób liniowy,
b) natężeniem wzrostów i spadków załamań krzywej sugerują szybkość zmiany poparcia.
Obie te sugestie wprowadzają w błąd, ponieważ nie mają poparcia w zebranych danych. Nie wiemy, co się dzieje pomiędzy sondażami.
Wizualizacja przedstawiona na rysunku 30 nie ma tych wad. Pokazuje niepewność pomiaru poprzez zaznaczenie przedziałów ufności, nie pokazuje jego środka, przez co nie pozwala na skupienie się na “łatwiejszej prawdzie”, jaką jest przyjęcie próbkowej częstości za poparcie, nie łączy łamaną kolejnych pomiarów, przez co nie tworzy wrażenia ani liniowości, ani zmienności.
Rysunek 29: Wyniki sondaży poparcia z zaznaczoną niepewnością za pomocą stopnia przezroczystości/rozmazania. Źródło: opracowanie własne

Wadą tej wizualizacji jest jednocześnie jej największa zaleta, nie daje ona prostej odpowiedzi na pytanie jak wygląda poparcie dla partii. A my chcemy wiedzieć! Po co nam wykres, który pokazuje tylko niepewność, ale z którego trudno odczytać komunikat gotowy do użycia.
Czy da się jakoś uzupełnić ten wykres tak, by możliwie wiarygodnie odpowiedzieć na pytanie, jak kształtuje się poparcie?
Przyjrzyjmy się dwóm skrajnym rozwiązaniom, pozwalającym na “wpisanie trendu” w ten wykres.
Pierwsze nazwę podejściem “szukającego sensacji”. W tym podejściu zakładamy, że poparcie dla partii zmienia się bardzo szybko, uznając za możliwe, że po każdej sensacyjnej (bardziej lub mniej) wiadomości pojawiającej się w mediach setki tysięcy ludzi zmienia zdanie. Przecież zmiana poparcia o 5% odpowiada zmianie zdania przez około milion Polaków.
Rysunek 30: Przedziały ufności dla poparcia w kolejnych sondażach. Źródło: opracowanie własne
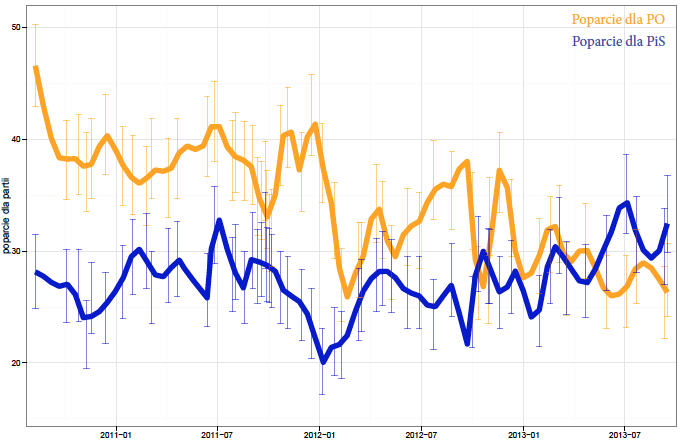
Drugie podejście nazwę podejściem “liniowego statystyka”, który wszystkie trendy upraszcza do liniowych zależności. Zakłada on, że poparcie jest niewrażliwe na epizody prezentowane w prasie i że w sposób liniowy rośnie lub maleje.
Rysunek 31: Przedziały ufności dla poparcia w kolejnych sondażach z wpisanym trendem. Trend został tak wybrany, by przechodził przez wszystkie wyniki sondaży. Źródło: opracowanie własne
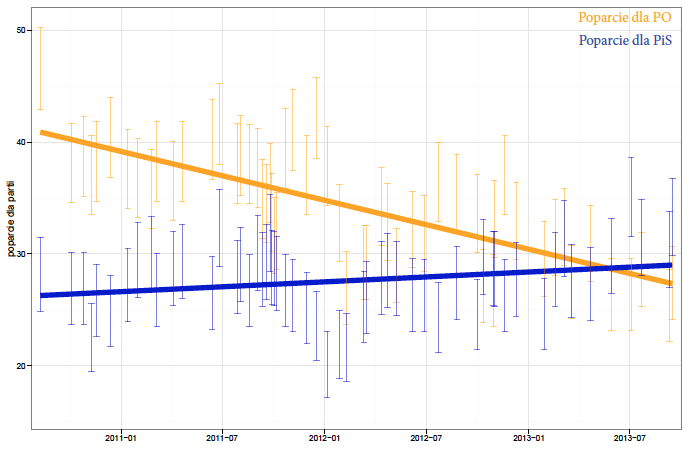
Oba te podejścia wydają się równie śmieszne i irracjonalne, choć ze smutkiem należy skonstatować, że mają niemałe grupy swoich zwolenników. No dobrze, ale czy można skonstruować bardziej “racjonalne” podejście? Czy jest jakaś szansa na oszacowanie trendu?
Okazuje się, że dużą pomocą będą przedziały ufności. Jeżeli przedstawiamy 90% przedziały, to średnio spodziewamy się, że pokryją nieznane szacowane poparcie partii politycznych w dziewięciu na dziesięć sondażach. W podejściu “szukającego sensacji” trend ani raz nie wyszedł poza przedziały ufności, w podejściu “liniowego statystyka” około jednej czwartej przedziałów znajduje się poza trendem.
Naturalnym rozwiązaniem jest znalezienie stopnia wygładzenia, który “przekroczy” przedziały ufności tylukrotnie, ile razy wynika to z ich szerokości.
Rysunek 32: Przedziały ufności dla poparcia w kolejnych sondażach z wpisanym liniowym trendem. Źródło: opracowanie własne
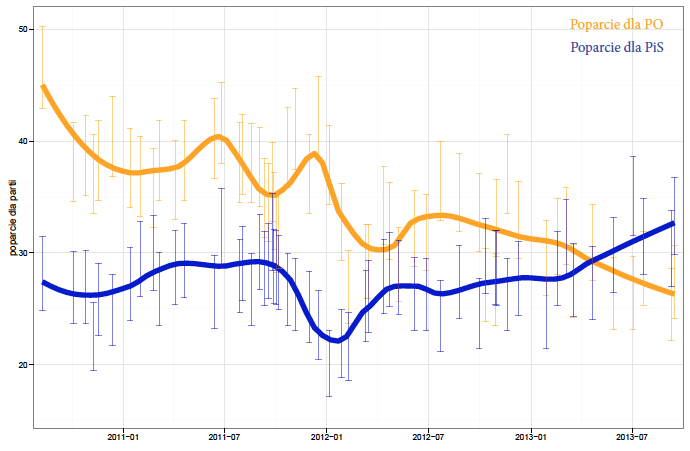
Jest to dosyć proste zadanie optymalizacyjne, które pozwala na wybranie pewnego rozsądnego stopnia wygładzenia wyników z kolejnych sondaży. Co więcej, można to podejście zastosować dla wyników sondażowych z różnych ośrodków badania opinii i zamiast śledzić wyniki z czterech ośrodków obserwować jedynie zachowanie wygładzonej średniej.
Stosując takie podejście dla danych z czterech ośrodków badania opinii publicznej (CBOS, TNS, SMG/KRC, HomoHomini) w okresie dwóch lat wyznaczono wygładzone poparcie pięciu największych partii.
Rysunek 33: Przedziały ufności dla poparcia w kolejnych sondażach z wpisanym trendem lokalnie wielomianowym. Przyjęto parametr wygładzający o wielkości 0,32, przez co dla 11/112 sondaży trend znajduje się poza przedziałem ufności (112 sondaży bierze się z 56 badań i po jednym sondażu dla każdej z dwóch partii w każdym badaniu). Źródło: opracowanie własne
Na wykresie 34 zaznaczono badane poparcie na tle wyników z poszczególnych sondaży. Każda kropka pokazuje wyniki poparcia dla jednej partii w jednym sondażu. Jak widzimy, często wynik pojedynczego sondażu jest daleko od uśrednionego trendu. Dokładnie tak, jak należałoby się tego spodziewać, zakładając ograniczoną dokładność pomiaru.
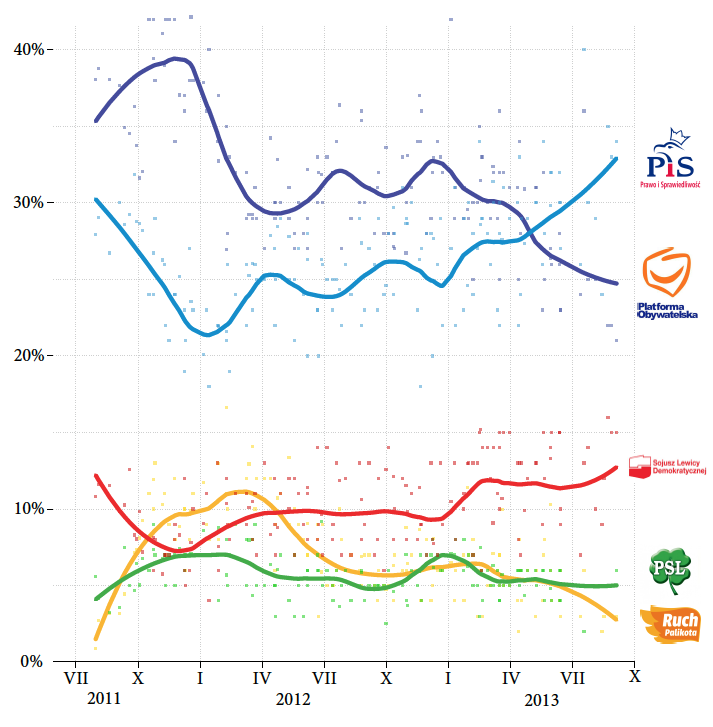
Rysunek 34: Poparcie dla pięciu największych partii w Polsce w okresie ostatnich dwóch lat. Poparcie uśrednione na bazie sondaży czterech największych agencji badania opinii publicznej. Źródło: opracowanie własne
Habitat
Poprzednie rozdziały dotyczyły projektowania grafiki statystycznej. W tym rozdziale zastanowimy się nad tym, w jakiej przestrzeni i jakiej formie funkcjonuje lub może funkcjonować grafika statystyczna i prezentacja danych. Czy wykresy tworzone są i oglądane wyłącznie na ekranie komputera?
Z pewnością nie, można je oczywiście wydrukować! Ale czy prezentacja danych może istnieć poza wydrukami i czy może funkcjonować w przestrzeni publicznej? A jeżeli tak, to na jakich zasadach?
Oryginalnym pomysłem na osadzenie grafiki statystycznej w przestrzeni publicznej są prace artystki Ellie Balk [Brooklyn public art, 2013] specjalizującej się w muralach. Sztuka uliczna (ang. street art), którą ona się zajmuje, znajduje miejsce dla grafiki statystycznej w codziennej miejskiej przestrzeni.
Jednym z, moim zdaniem, ciekawszych projektów tej artystki jest Weather Mural przedstawiający dzienną zmienność temperatur w dziesięciu wybranych latach. Sama grafika, gdyby pozostała w komputerze, nie robiłaby dużego wrażenia. Ale po naniesieniu jej na mur okazuje się, że odkrywa zupełnie nowe możliwości interakcji pomiędzy informacją na wykresie a potencjalnym odbiorcą.
 Rysunek 35: Proces tworzenia malunku Weather Mural Źródło: http://elliebalk.com/weathermural/
Rysunek 35: Proces tworzenia malunku Weather Mural Źródło: http://elliebalk.com/weathermural/

Kiedy przechodzimy koło tego murala, pojawia się w nas naturalna chęć sprawdzenia pogody w dniu urodzin lub innym charakterystycznym dniu przedstawionym na murze. Również sam sposób powstawania murala był interesujący. Ostatni prezentowany rok – 2060, dotyczy prognozy temperatury w przyszłości. Zadanie wyznaczenia prognozy spoczęło na barkach uczniów, dla których było to zadaniem domowym. A następnie ta praca domowa przerodziła się w część tego wielkiego murala, który w dodatku mogli sami namalować. To bardzo interesujący sposób interakcji z danymi wykraczający daleko poza standardowe oglądania wykresów na komputerze.
Rodzi się więc pytanie na czym lub z czego można tworzyć prezentacje danych. Jednym z bardziej wdzięcznych tworzyw, pozwalających na prostą budowę a jednocześnie precyzyjną prezentację, są klocki LEGO (lub inne podobne klocki).
Rysunek 36: Mural Weather Mural Przedstawiono wykresy temperatur w Nowym Jorku w dziesięciu wybranych latach pomiędzy rokiem 1930 a 2060. Mural wykorzystuje fakturę ściany cegieł jako siatkę pomocniczą ułatwiającą odczytanie temperatury w konkretnym dniu konkretnego miesiąca. Źródło: http://elliebalk.com/weathermural/
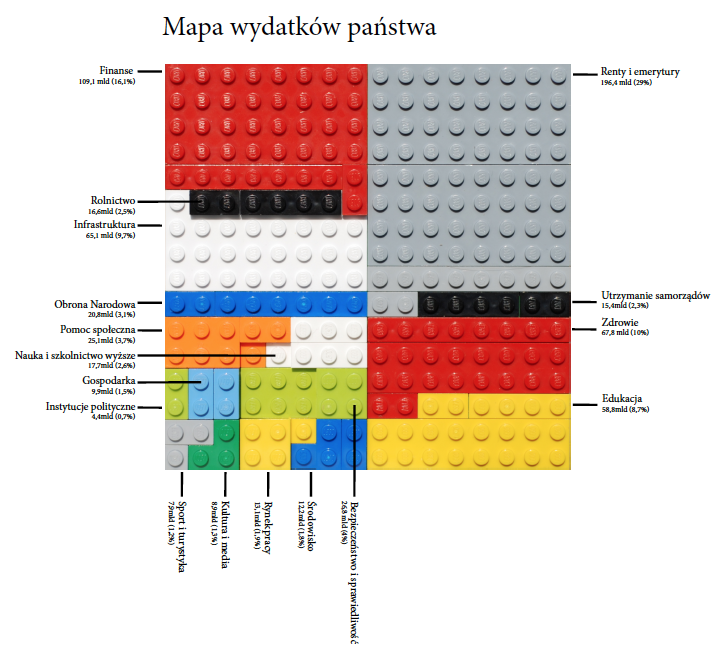
Na rysunku 37 przedstawiamy mapę wydatków Polski w roku 2012. Każda kategoria wydatków została przedstawiona przez klocki innego koloru. Pole zajęte przez określony kolor odpowiada wielkości wydatków. Taką mapę lub inną formę wizualizacji mogą wykonać samodzielnie nawet młode osoby, dzięki czemu bawiąc się, wchodzą w bezpośrednią interakcję z danymi. Również dla dorosłych to ciekawy sposób wizualizacji danych. Triada “zaprojektuj – wyszukaj – zbuduj” jest tak samo atrakcyjna, gdy chodzi o zabawę klockami jak i gdy chodzi o opracowywanie wizualizacji danych.
Innym materiałem, który można wykorzystać do zabawy w wizualizacje danych jest śnieg.
W Kanadzie dosyć popularne są wystawy rzeźb wykonanych z bloków lodu. Dlaczego lodu lub śniegu nie wykorzystać do wykonania wykresu statystycznego?
Więcej o wykresach ze śniegu można przeczytać w artykule Śniegowy wykres słupkowy a oparta o dane dyskusja o finansowaniu nauki, SmarterPoland.pl, http://bit.ly/14ozEc7.
Rysunek 37: Mapa wydatków państwa przedstawiona za pomocą klocków. Źródło: opracowanie własne

Rysunek 38: Mobilność naukowców w różnych krajach przedstawiona za pomocą wykresu śniegowego. Źródło: opracowanie własne
Równie dobrze zamiast śniegu można używać piasku czy układanych w stos kamieni. Taka forma oczywiście zazwyczaj nie wnosi niczego nowego do wyników, jest jedynie ciekawą alternatywą w interakcji z danymi, co samo w sobie wystarczy, by pobudzić dodatkowe zainteresowanie odbiorcy.
Jeżeli nie śnieg i nie LEGO, to może wycinanki przyczepione za pomocą magnesów do tablicy magnetycznej? W jednym z projektów do przedstawienia liczby, przydatności bojowej czy prędkości okrętów będących na wyposażeniu Polskiej Marynarki Wojennej wykorzystano tablicę magnetyczną, wycięte obrysy statków i magnesy.
 Rysunek 39: Kawałki układanki z rysunku 40. Źródło: opracowanie własne}
Rysunek 39: Kawałki układanki z rysunku 40. Źródło: opracowanie własne}
Tworzenie wykresów z użyciem magnesów i magnetycznej ściany może być formą prototypowania docelowej wizualizacji danych, ułatwia szybkie zobaczenie, jak docelowy wykres może wyglądać, a może pełnić rolę zabawową lub edukacyjną, gdy uczymy się czy to technik prezentacji danych czy informacji o marynarce wojennej. Aby dobrze pokazać informację, trzeba ją najpierw zrozumieć. Budowa wizualizacji jest więc świetnym połączeniem zabawy i edukacji.
Szerszy opis projektu i sylwetki statków do samodzielnej pracy są do pobrania ze strony SmarterPoland.pl, Marynarka Wojenna Polski, trzy gry statystyczne dla dzieci, http://bit.ly/1f5fb1k
 Rysunek 40: Prędkość okrętów będących na wyposażeniu Polskiej Marynarki Wojennej. Względne położenie okrętów w skali 1:500 po jednej minucie od wspólnego startu
Rysunek 40: Prędkość okrętów będących na wyposażeniu Polskiej Marynarki Wojennej. Względne położenie okrętów w skali 1:500 po jednej minucie od wspólnego startu
Obiekty codziennego użytku możemy wykorzystać nie tylko do budowania z nich wykresów, ale również jako nośniki informacji. Przykładem użycia obiektu codziennego użytku jako medium dla wykresów jest Projekt Kubek fundacji SmarterPoland.pl, którego celem było przedstawienie na powierzchni kubka zbioru interesujących statystyk dotyczących Polski w taki sposób, by najciekawsze informacje zawsze były “pod ręką”.
Taki kubek może pełnić funkcję informacyjną, można się czegoś o Polsce z takiego kubka dowiedzieć. Jeżeli jest wystarczająco bogaty w informacje, to można je odkrywać podczas porannej kawy. Interesującym problemem przy projektowaniu takiego kubka był zarówno wybór statystyk do przedstawienia, jak i sposób upakowania ich na niewielkiej powierzchni, którą można na kubku zadrukować
Jeżeli chodzi o wybór prezentowanych wskaźników, to w ostatniej wersji wybrano zbiór danych opisujących finanse, demografię, edukację, sport czy zdrowie mieszkańców Polski. Celowa różnorodność mająca w zamierzeniu pokazać jak wieloaspektowym organizmem jest nasz kraj.
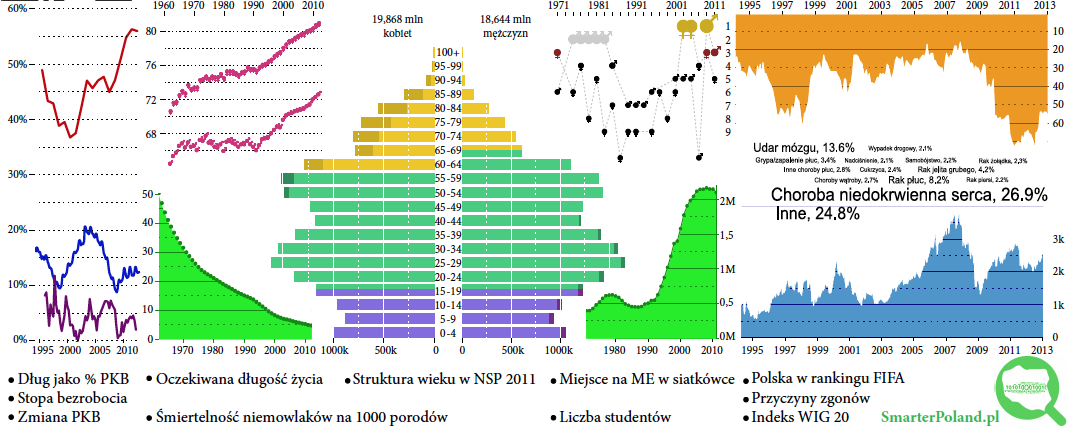 Rysunek 41: Projekt kubek. Rozmieszczenie jedenastu statystycznych infografik o Polsce na kubku. Źródło: opracowanie własne
Rysunek 41: Projekt kubek. Rozmieszczenie jedenastu statystycznych infografik o Polsce na kubku. Źródło: opracowanie własne
Co ciekawe, pomimo iż część z prezentowanych informacji szybko się starzeje, po roku używania tego kubka w codziennych czynnościach muszę przyznać, że wciąż jest źródłem inspiracji. To zaskakujące, jak często przydaje się informacja o strukturze wiekowej populacji, która jest zawsze pod ręką gdy mamy taki kubek.
Zaprojektowanie każdego z tych wykresów wymagało iteracyjnej pracy. Zmieniano zarówno wygląd, jak i wymiary wykresu, który nie tylko musiał być czytelny, ale musiał być spójny z otaczającymi go wykresami. Ponieważ ten esej poświęcony jest ścieżkom, przedstawię dla czterech wybranych wykresów z tego projektu ich metamorfozy od pierwszego elektronicznego szkicu po postać finalną, która znalazła się na kubku.
Jednym z wykresów przedstawionych na kubku jest piramida populacyjna. Bardzo często jest ona przedstawiana w postaci dwóch wykresów paskowych zestawionych ze sobą w ten sposób, by pozycja względem osi pionowej odpowiadała grupie wiekowej, a długość paska – liczebności określonej frakcji populacji. Trzy podstawowe pytania, na które odpowiedzi szuka się na piramidzie wieku, to porównanie udziału kobiet do mężczyzn w określonej grupie wiekowej (np. czy jest więcej 50-letnich kobiet, czy mężczyzn), porównywanie grup wiekowych (czy jest więcej osób w wieku do 20 lat, czy w wieku od 20 do 40 lat) oraz ocena, jak dużo jest osób w określonej grupie wiekowej (ile jest osób w wieku produkcyjnym).
 Rysunek 42: Tak wygląda kubek z Projektu Kubek
Rysunek 42: Tak wygląda kubek z Projektu Kubek
Aby ułatwić odpowiedź na te trzy pytania, na piramidzie populacyjnej warto zaznaczyć, jak duża jest “nadwyżka” jednej płci nad drugą (zrealizowane za pomocą innego koloru) oraz dodać linie pomocnicze ułatwiające ocenę długości paska (dodanie tych linii za pomocą białego koloru nie zaśmieca wykresu).
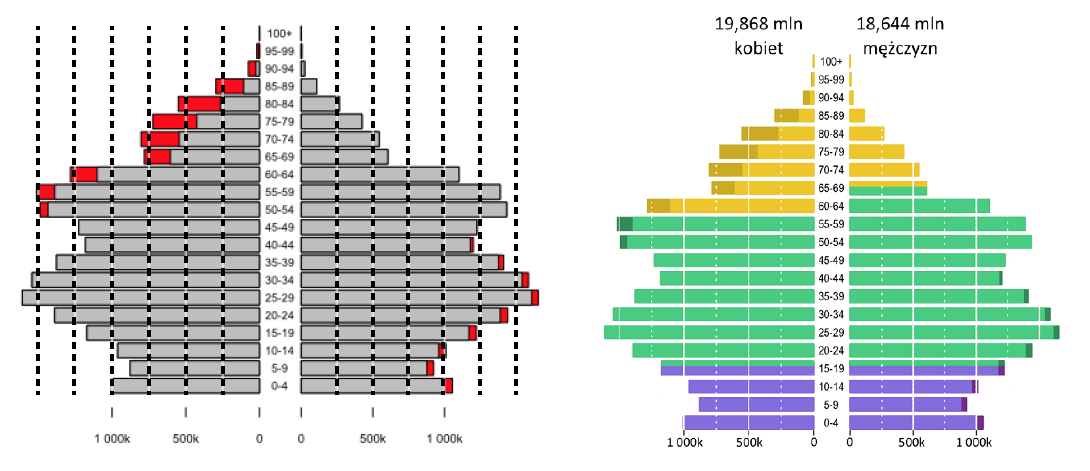 Rysunek 43: “Przed i po”, czyli lifting wykresu prezentującego piramidę wiekową populacji Polski na rok 2011. Źródło: opracowanie własne
Rysunek 43: “Przed i po”, czyli lifting wykresu prezentującego piramidę wiekową populacji Polski na rok 2011. Źródło: opracowanie własne
Dalszy retusz wykresu piramidy wieku obejmował zaznaczenie za pomocą kolorów okresów uznawanych za: wiek przedprodukcyjny, produkcyjny i poprodukcyjny oraz ogólny lifting polegający na zwiększeniu wielkości napisów, zwiększeniu czytelności wykresów przez odpowiedni dobór kolorów pasków oraz dodanie podsumowań w stylu sumaryczna liczba kobiet i mężczyzn.
Innym wykresem przedstawionym na kubku jest pozycja Polski w rankingu FIFA, czyli Międzynarodowej Federacji Piłki Nożnej (FIFA od fr. Fédération Internationale de Football Association). Główne pytania interesujące odbiorcę tego wykresu to: na jakiej pozycji jesteśmy aktualnie oraz kiedy pozycja naszego kraju zmieniała się (poprawiała lub pogarszała) najszybciej. Aby móc odczytać pozycję kraju, przydatne są dodatkowe pomocnicze linie siatki.
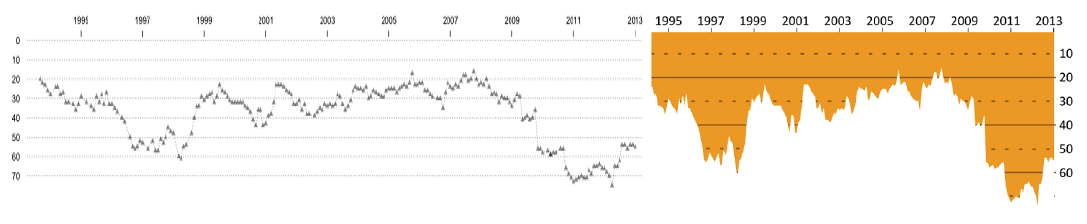 Rysunek 44: “Przed i po”, czyli lifting wykresu prezentującego pozycje reprezentacji Polski w rankingu FIFA. Źródło: opracowanie własne
Rysunek 44: “Przed i po”, czyli lifting wykresu prezentującego pozycje reprezentacji Polski w rankingu FIFA. Źródło: opracowanie własne
Retusz wykresu przedstawiającego pozycję w rankingu FIFA dotyczył trzech głównych zmian. Ściśnięcie wykresu pozwoliło na zaoszczędzenie miejsca bez utraty informacji. Ustawienie osi tak, by kolejne pozycje biegły z góry (miejsce pierwsze) w dół, również było pomocne, ponieważ intuicyjnie doczytujemy, że im niżej na wykresie tym gorsza sytuacja, a więc i niższe miejsca w rankingu. Kolejna zmiana polegała na zastąpieniu łamanej przez zamalowany obszar. Takie rozwiązanie pozwala zarówno ukryć niepotrzebne fragmenty linii pomocniczych, jak i łatwo porównywać skalę spadku w rankingu. Co prawda pozycja w rankingu nie jest zmienną na skali ilorazowej (pozycja 20. nie jest dwa razy lepsza niż pozycja 40.), ale w tym przypadku zaznaczenie odległości od szczytu rankingu za pomocą długości linii ułatwia szybką orientację co do pozycji w rankingu.
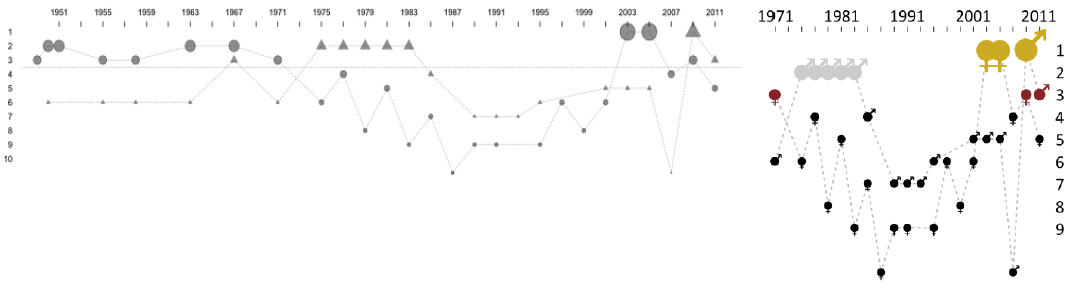 Rysunek 45: “Przed i po”, czyli lifting wykresu prezentującego pozycje reprezentacji Polski w mistrzostwach piłki siatkowej. Źródło: opracowanie własne
Rysunek 45: “Przed i po”, czyli lifting wykresu prezentującego pozycje reprezentacji Polski w mistrzostwach piłki siatkowej. Źródło: opracowanie własne
Nasza reprezentacja w piłce siatkowej, tak męska jak i żeńska, radzi sobie lepiej niż reprezentacja piłki nożnej. O ile w rankingu FIFA nasza pozycja jest słaba i zastanawiamy się, jak pokazać spadek z 40. miejsca na miejsce 70., to w przypadku mistrzostw piłki siatkowej możemy skupić się na zliczaniu zdobytych medali i ich kolorów. Pytania, na które chcemy móc odpowiedzieć po lekturze tego wykresu to: jakie medale w którym roku zdobyła nasza reprezentacja oraz czy była to reprezentacja kobiet czy mężczyzn
Retusz wykresu dotyczącego piłki siatkowej składał się z kilku głównych kroków. Pierwszym było ściśnięcie wykresu i powiększenie napisów, by były wyraźniejsze. Ponieważ najbardziej interesują nas pozycje medalowe, więc wyniki dotyczące medali zostały wyróżnione, wielkością oraz kolorem punktu oznaczającym kolor zdobytego medalu. Ponieważ przedstawiamy wyniki dla kobiet i mężczyzn, na wykresie powinna znajdować się legenda. Ale aby oszczędzić miejsce, zdecydowałem się na wybranie symboli, które jednoznacznie będą się kojarzyły z płcią. Ponieważ w grę wchodziło przedstawienie tylko pierwszych dziesięciu pozycji w rankingu, udało się również zrezygnować z linii pomocniczych, które nie są tu niezbędne, a gdyby zostały dodane, zmniejszyłyby czytelność wykresu.
Ostatnim wykresem z Projektu Kubek, który tutaj omówimy, jest prezentacja najczęstszych przyczyn zgonów. Ten temat wydaje się być prosty do prezentacji, ale okazuje się, że jest to pozorna prostota. Podobnie jak w poprzednich wykresach, zanim narysujemy pierwszą kreskę należy zastanowić się, jakiego rodzaju pytania zadawać będzie sobie osoba czytająca ten wykres. Trzy główne pytania to: co jest najczęstszą przyczyną zgonów, jakie są kolejne pod względem częstości przyczyny zgonów i na ile jedna przyczyna zgonów jest rzadsza niż inna. Na każde z tych pytań można odpowiedzieć, jeżeli dane zaprezentujemy z użyciem wykresu paskowego.
 Rysunek 46: “Przed i po”, czyli lifting wykresu prezentującego najczęstsze przyczyny zgonów w Polsce. Źródło: opracowanie własne
Rysunek 46: “Przed i po”, czyli lifting wykresu prezentującego najczęstsze przyczyny zgonów w Polsce. Źródło: opracowanie własne
Ten wykres paskowy nie jest atrakcyjny wizualnie. Przypomina dwa rogi i coś pomiędzy. Retusz tego wykresu doprowadził do zamiany pasków na chmurę słów, w której wielkością napisu zaznacza się też względną częstość danej przyczyny zgonu. Wielkość czcionki jest charakterystyką, którą odczytuje się z małą dokładnością (dlatego częstość zgonów jest również wyrażona liczbą), ale końcowy efekt jest ciekawy
Powyższe przykłady dotyczyły materiałów, z których budować można wykresy, lub przestrzeni, w których te wykresy można umieszczać. Ostatnim przykładem w tym rozdziale jest projekt wykresu, który nawet po wydrukowaniu pozwala na wejście w interakcję z danymi.
Przedstawiony poniżej projekt bardzo mnie cieszy, ponieważ został wykonany dla poważnej instytucji – Organizacji Współpracy Gospodarczej i Rozwoju, oraz pokazany podczas prezentacji na kilku konferencjach. Projekt dotyczy danych z badania PISA 2012 przeprowadzanego przez organizację OECD w ponad 65 krajach. Jednym z wyników tego badania jest ocena średniego poziomu umiejętności matematycznych 10-latków w każdym z krajów, ale wyników szczegółowych dla każdego kraju jest więcej.
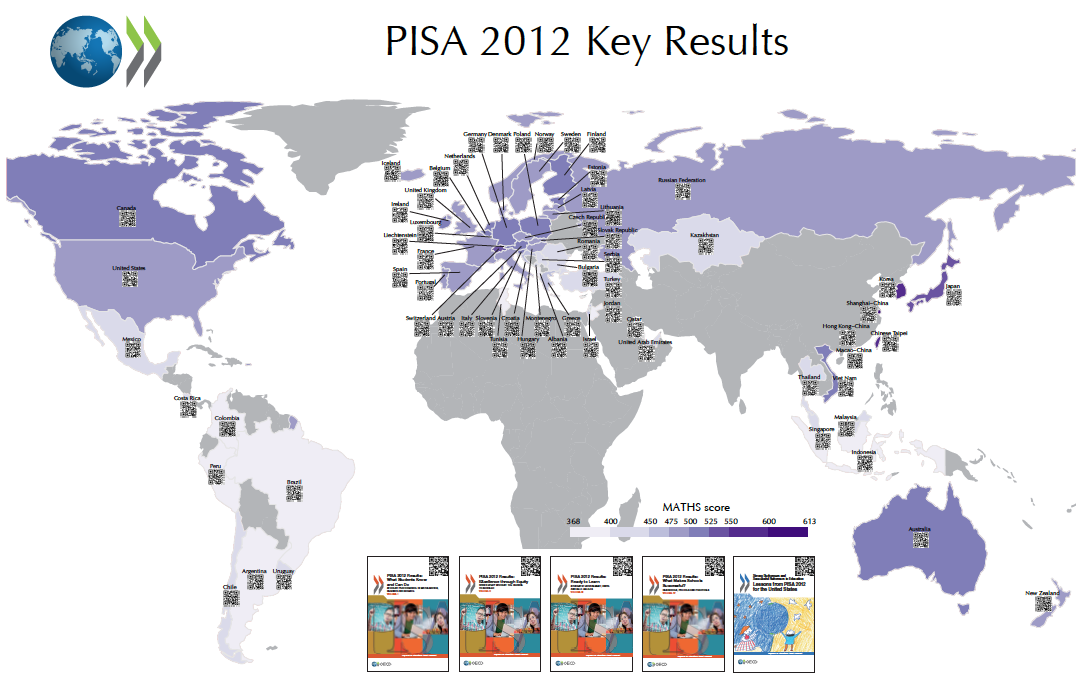 Rysunek 47: Średnia ocena umiejętności matematycznych badania PISA 2012 dla różnych krajów. Kody QR umieszczone na tym wykresie prowadzą do szczegółowych informacji na temat określonego kraju. Źródło: opracowanie własne
Rysunek 47: Średnia ocena umiejętności matematycznych badania PISA 2012 dla różnych krajów. Kody QR umieszczone na tym wykresie prowadzą do szczegółowych informacji na temat określonego kraju. Źródło: opracowanie własne
Aby umożliwić łatwy dostęp do szczegółowych danych o określonym kraju, wykorzystano kody QR (ang. Quick Response), które są w stanie zakodować niewielki tekst, na przykład odnośnik do strony internetowej. Takie odnośniki można odczytać z użyciem telefonu komórkowego lub tabletu z odpowiednią aplikacją do rozpoznawania kodów QR. Każdy kod prowadzi do strony internetowej ze szczegółową informacją o danym kraju. Tłem dla tych kodów jest kartogram, na którym zakodowano średni wynik z umiejętności matematycznych za pomocą koloru.
Cały wykres zamienił się w interfejs dostępu do bardziej szczegółowych statystyk. Wydrukowany jako wielkoformatowy plakat o rozmiarze ponad 3 metrów kwadratowych i powieszony na korytarzu konferencyjnym lub przed pokojem dyrektora pozwala na zainteresowanie tematem oraz dostęp do szczegółowych informacji poprzez zeskanowanie kodu QR telefonem komórkowym. Statyczny wydruk staje się tym samym graficznym spisem treści i skorowidzem w jednym.
Dlaczego?
Przyzwyczajeni jesteśmy do myślenia, że cykl życia statystycznej prezentacji danych zaczyna się i kończy na ekranie monitora, że do tworzenia wykresów wykorzystuje się arkusz kalkulacyjny, a najlepszą formą prezentacji są wykresy kołowe lub paskowe. Ale informacja chce być pokazywana. I jeżeli jest ciekawa, to chce być pokazana w ciekawy sposób.
Wykresy ze śniegu, piasku, kamieni, klocków LEGO czy kodów QR mogą wyglądać dziwnie, ponieważ są rzadko spotykane. Dlatego też najłatwiej usprawiedliwić prace nad nimi, mówiąc, że jest to tylko zabawa.
Wierzę jednak, że z takiej zabawy polegającej na poszukiwaniu nowych sposobów przedstawienia określonej informacji mogą powstać ciekawe rozwiązania. Dostępne dziś drukarki 3D mogą być wykorzystane do drukowania prawdziwie trójwymiarowych reprezentacji danych. Aspekt czasu na wykresie można zaznaczyć zamieniając wykres w animacje (czas pojawia się jako dodatkowy wymiar) lub zestaw wykresów, które po wydrukowaniu można kartkować. Niepewność na wykresie można zaznaczyć rozmazaniem linii, serią alternatywnych trajektorii lub coraz to bledszym kolorem obrazującym nasz brak pewności co do określonych wartości.
Praca z wizualizacją to uszczegóławianie pytania badawczego, na które wizualizacja ma odpowiedzieć, a następnie eksperymentowanie z prezentacją danych, która odpowiada na postawione pytanie. Nie ograniczajmy się w tych eksperymentach tylko do doboru kolorów na wykresie kołowym.
Nawet jeżeli niektóre z eksperymentów po początkowym okresie fascynacji uznamy za kompletne porażki, to wciąż najważniejsze jest, by uczyć się tak z sukcesów jak i porażek.
 Rysunek 48: Zdjęcie prawdziwie trójwymiarowego wykresu kołowego z lotniska w Zurychu. Wykres przedstawia ilość emitowanego CO2}
Rysunek 48: Zdjęcie prawdziwie trójwymiarowego wykresu kołowego z lotniska w Zurychu. Wykres przedstawia ilość emitowanego CO2}